|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Традиционные шифры с симметричным ключом
Криптоанализ шифра Виженера
Шифры Виженера, подобно всем многоалфавитным шифрам, не сохраняют частоту символов. Однако Ева может использовать некоторые методы для того, чтобы расшифровать перехваченный зашифрованный текст. Криптоанализ в данном случае состоит из двух частей: находят длину ключа и потом непосредственно находят ключ.
- Были изобретены несколько методов, чтобы найти длину ключа. Один метод рассмотрим ниже. В так называемом тесте Казиского (Kasiski) криптоаналитик в зашифрованном тексте ищет повторные сегменты по крайней мере из трех символов. Предположим, что найдены два сегмента, и расстояние между ними d. Криптоаналитик предполагает, что m делит d, где m — длина ключа. Если можно найти больше повторных сегментов с расстоянием d1, d2, …., dn, тогда НОД(d1, d2, …., dn....)/ m. Это предположение логично, потому что если два символа одинаковы и
 (k = 1, 2...) — символы, выделенные в исходном тексте, то одинаковы и
(k = 1, 2...) — символы, выделенные в исходном тексте, то одинаковы и  символы, выделенные в зашифрованном тексте. Криптоаналитик использует сегменты по крайней мере из трех символов, чтобы избежать случаев, где символы имеют один и тот же ключ. Пример 4.20 может помочь нам п
онять эти рассуждения.
символы, выделенные в зашифрованном тексте. Криптоаналитик использует сегменты по крайней мере из трех символов, чтобы избежать случаев, где символы имеют один и тот же ключ. Пример 4.20 может помочь нам п
онять эти рассуждения. - После того как длина ключа была найдена, криптоаналитик использует идею, показанную в примере 4.18. Здесь зашифрованный текст делится на m различных частей и применяется метод, используемый в криптоанализе аддитивного шифра, включая атаку частоты. Каждая часть зашифрованного текста может быть расшифрована и соединена с другими, чтобы создать целый исходный текст, другие слова. Весь зашифрованный текст не сохраняет частоту отдельной буквы исходного текста, но каждая часть делает это.
Пример 4.19
Предположим, что мы перехватили следующий зашифрованный текст:
LIOMWGFEGGDVWGHHCQUCRHRWAGWIOWQLKGZETKKMEVLWPCZVG'TH VTSGXQOVGCSVETQLTJSUMVWVEUVLXEWSLGFZMVVWLGYHCUSWXQH - KVGSHEEVFLCFDGVSUMPHKIRZDMPHHBVWVWJWIXGFWLTSHGJOUEEHH- VUCFVGOWICQLIJSUXGLW
Тест Казиского на повторение сегментов на три символа приводит к результатам, показанным в таблице 4.4.
| Комбинация | Первое расстояние | Второе расстояние | Разность |
|---|---|---|---|
| JSU | 68 | 168 | 100 |
| SUM | 69 | 117 | 48 |
| VWV | 72 | 132 | 60 |
| MPH | 119 | 127 | 8 |
Наибольший делитель - 4, что означает длину ключа, пропорциональную 4. Сначала пробуем m = 4. Делим зашифрованный текст на четыре части. Часть C1 состоит из символов 1, 5, 9...; часть C2 состоит из символов 2, 6, 10..., и так далее. Используем статистическую атаку каждой части отдельно. Перебираем расшифровывающиеся части по одному символу одновременно, чтобы получить целый исходный текст.
| С1 | LWGW | CRAO | KTEP | GTQC | TJVU | EGVG | UQGE | CVPR | PVJG | TJEU | GCJG |
| P1 | jueu | apym | ircn | eroa | rhts | thin | ytra | hcie | ixst | hcar | rehe |
| C2 | IGGG | QHGW | GKVC | TSOS | QSWV | WFVY | SHSV | FSHZ | HWWF | SOHC | OQSL |
| P2 | usss | ctsl | swho | feae | ceih | cete | soec | atnp | nkhe | rhck | esex |
| C3 | OFDN | URWQ | ZKLZ | HGVV | LUVL | SZWH | WKHF | DUKD | HVIW | HUHF | WLUW |
| P3 | lcae | rotn | whiw | edss | irsi | irh | eteh | retl | tiid | eatr | airt |
| C4 | MEVN | CWIL | EMWV | VXGE | TMEX | LMLC | XVEL | GMIM | BWHL | GEVV | ITX |
| P4 | iard | yseh | aisr | rtca | piaf | pwte | thec | arha | esft | erec | tpt |
Если исходный текст не имеет смысла, попробуем с другим m.
В рассматриваемом случае исходный текст имеет смысл (читаем по столбцам).
Перевод этого текста приведен ниже.
Шифр Хилла
Другой интересный пример многоалфавитного шифра — шифр Хилла, изобретенный Лестером С. Хиллом. В отличие от других многоалфавитных шифров, которые мы уже рассмотрели, здесь исходный текст разделен на блоки равного размера. Блоки зашифрованы по одному таким способом, что каждый символ в блоке вносит вклад в шифрование других символов в блоке. По этой причине шифр Хилла принадлежит к категории шифров, названных блочными шифрами. Другие шифры, которые мы изучали до сих пор, принадлежат к категории, называемой шифры потока. Отличие между шифрами блока и шифрами потока обсуждаются в конце этой лекции.
В шифре Хилла ключ — квадратная матрица размера 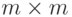 ., в котором m. является размером блока. Если мы вызываем ключевую матрицу K, то каждый элемент ki,j определяется матрицей, как показано на рис. 4.15.
., в котором m. является размером блока. Если мы вызываем ключевую матрицу K, то каждый элемент ki,j определяется матрицей, как показано на рис. 4.15.
Покажем, как получается один блок зашифрованного текста. Если мы обозначим m символов блоков исходного текста P1, P2 ..., Pm, соответствующие символы в блоках зашифрованного текста будут C1, C2 , ..., Cm. Тогда мы имеем
C1 = P1k11+P2k21+……+Pmkm1 C2 = P1k12+P2k22+……+Pmkm2 ……………………………………………………… Cm = P1k1m+ P2k2m +……+ Pmkmm
Уравнения показывают, что каждый символ зашифрованного текста, такой, как C1, зависит от символов всего исходного текста в блоке (P1, P2,..., Pm). Однако мы должны знать, что не все квадратные матрицы имеют мультипликативные инверсии в Z26, так что Алиса и Боб должны быть осторожны в выборе ключа. Боб не сможет расшифровать зашифрованный текст, передаваемый Алисой, если матрица не имеет мультипликативной инверсии.
Пример 4.20
Использование матриц позволяет Алисе зашифровать весь исходный текст. В этом случае исходный текст  — матрица, в которой l является номером блоков. Например, исходный текст "code is ready" ("код готов"), может быть представлен как матрица
— матрица, в которой l является номером блоков. Например, исходный текст "code is ready" ("код готов"), может быть представлен как матрица  при добавлении дополнительного фиктивного символа "z" к последнему блоку и удалении пробелов; зашифрованный текст выглядит как "OHKNIHGKLISS". Боб может расшифровать сообщение, используя инверсную матрицу-ключ. Шифрование и дешифрование показано на рис. 4.16.
при добавлении дополнительного фиктивного символа "z" к последнему блоку и удалении пробелов; зашифрованный текст выглядит как "OHKNIHGKLISS". Боб может расшифровать сообщение, используя инверсную матрицу-ключ. Шифрование и дешифрование показано на рис. 4.16.
Криптоанализ шифров Хилла
Криптоанализ только для зашифрованного шифрами Хилла текста труден. Во-первых, атака грубой силы при шифре Хилла чрезвычайно сложна, потому что матрица-ключ — 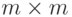 . Каждый вход может иметь одно из 26 значений. Во-первых, это означает размер ключа
. Каждый вход может иметь одно из 26 значений. Во-первых, это означает размер ключа  . Однако, не все матрицы имеют мультипликативную инверсию. Поэтому область существования ключей все же не такая огромная.
. Однако, не все матрицы имеют мультипликативную инверсию. Поэтому область существования ключей все же не такая огромная.
Во-вторых, шифры Хилла не сохраняют статистику обычного текста. Ева не может провести анализ частоты отдельных букв из двух или трех букв. Анализ частоты слов размера m мог бы cработать, но очень редко исходный текст имеет много одинаковых строк размера m. Ева, однако, может провести атаку на шифр, используя метод знания исходного текста, если она знает значение m и знает пары "исходный текст/зашифрованный текст", по крайней мере m блоков. Блоки могут принадлежать тому же самому сообщению или различным сообщениям, но должны быть различны. Ева может создать две 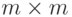 . матрицы, P (обычный текст) и C (зашифрованный текст), в котором соответствующие строки представляют известные пары обычного/зашифрованного текста. Поскольку C = PK, Ева может использовать отношения K = CP-1, чтобы найти ключ, если P является обратимым. Если P
не является обратимым, то Ева должна задействовать различные наборы m пар обычного/зашифрованного текста.
. матрицы, P (обычный текст) и C (зашифрованный текст), в котором соответствующие строки представляют известные пары обычного/зашифрованного текста. Поскольку C = PK, Ева может использовать отношения K = CP-1, чтобы найти ключ, если P является обратимым. Если P
не является обратимым, то Ева должна задействовать различные наборы m пар обычного/зашифрованного текста.
Если Ева не знает значение m, она может попробовать различные значения при условии, что m не является очень большим.
Пример 4.21
Предположим, что Ева знает, что m = 3. Она перехватила три пары блока исходного/зашифрованного текста (не обязательно из того же самого сообщения), как показано на рис. 4.17.
Она составляет матрицы P и C из этих пар. Поскольку в данном случае матрица P обратима, она инвертирует эту матрицу и умножает ее на C, что дает матрицу ключей K, как это показано на рис. 4.18.
Теперь она имеет ключ и может взломать любой шифрованный текст, где применен этот ключ.
Одноразовый блокнот
Одна из целей криптографии — идеальная секретность. Исследования Шеннона показали, что идеальная секретность может быть достигнута, если символы исходного текста зашифрованы с помощью ключа, выбранного случайно из некоторой области ключей. Например, аддитивный шифр может быть легко взломан, потому что используется один и тот же ключ. Но даже и этот шифр может быть идеальным, если ключ, который применяется для шифрования каждого символа, выбран случайно из множества ключей (00, 01, 02.... 25): если первый символ зашифрован с помощью ключа 04, второй символ — с помощью ключа 02, третий — с помощью ключа 21, и так далее. Атака "только для зашифрованного текста" становится невозможна. Если передатчик изменяет ключ, используя каждый раз иную случайную последовательность целых чисел, другие типы атак также будут невозможны.
Эта идея используется в шифре, который называется одноразовым блокнотом. Его изобрел американский инженер Вернам. В этом шифре ключ имеет ту же самую длину, что и исходный текст, и выбран совершенно случайно.
Одноразовый блокнот — идеальный шифр, но его почти невозможно реализовать коммерчески. Если ключ каждый раз генерируется заново, как Алиса может каждый раз сообщать Бобу новый ключ? Для этого каждый раз нужно передавать сообщение. Однако есть некоторые случаи, когда возможно использование одноразового блокнота. Например, если президент страны должен передать полностью секретное сообщение президенту другой страны, он может перед посылкой сообщения передать с помощью доверенного посланника случайный ключ. Некоторые вопросы изменения шифра одноразового блокнота обсуждаются в дальнейших лекциях, когда будет рассматриваться введение в современную криптографию.
Роторный шифр
Хотя шифры одноразового блокнота не применяются на практике, один шаг от него к более защищенному шифру — роторный шифр. Он возвращается к идее моноалфавитной подстановки, но меняет принцип отображения исходного текста в символы зашифрованного текста для каждого символа исходного текста. Рисунок 4.19 показывает упрощенный пример роторного шифра.
Ротор, показанный на рис. 4.19, применен только для 6 букв, но реальные роторы используют 26 букв. Ротор постоянно связывает символы исходного и зашифрованного текстов, но подключение обеспечивается щетками. Обратите внимание, что соединение символов исходного и зашифрованного текстов показано так, как если бы ротор был прозрачен и можно было видеть внутреннюю часть.
Начальная установка (позиция) ротора — ключ засекречивания между Алисой и Бобом — это зашифрованный первый символ исходного текста. Используя начальную установку, второй символ зашифрован после того, как проведено первое вращение (на рис. 4.19 — это поворот на 1/6 круга, на реальной установке — поворот на 1/26 ), и так далее.
Слово с тремя буквами, такими как "bee", зашифровано как "BAA", если ротор неподвижен (моноалфавитный шифр подстановки), но оно будет зашифровано как "BCA", если он вращается (роторный шифр). Это показывает, что роторный шифр — многоалфавитный шифр, потому что два появления того же самого символа исходного текста зашифрованы как различные символы.
Роторный шифр является стойким к атаке грубой силы, как моноалфавитный шифр подстановки, потому что Ева должна найти первое множество отображений среди возможных 26! (факториал). Роторный шифр является намного более стойким к статистической атаке, чем моноалфавитный шифр подстановки, потому что в нем не сохраняется частота употребления буквы.
Машина "Энигма"
Машина "Энигма" была первоначально изобретена в Сербии, но была изменена специалистами немецкой армии и интенсивно использовалась в течение Второй Мировой Войны. Машина базировалась на принципе шифров ротора. Рисунок 4.20 показывает упрощенную схему построения машины.
Ниже перечислены главные компоненты машины.
- Клавиатура с 26 -ю ключами, используемыми для того, чтобы вводить исходный текст при шифровании, и для того, чтобы вводить зашифрованный текст при расшифровке.
- Ламповая панель с 26 -ю лампами, которая показывает символы зашифрованного текста при шифровании и символы исходного текста при дешифровании.
- Коммутационная панель с 26 -ю штепселями, вручную подключенными 13 -ю проводами. Конфигурация изменяется каждый день, чтобы обеспечить различное скрэмблирование.
- Три замонтированных ротора, такие же как рассмотренные в предыдущей секции. Эти три ротора выбираются ежедневно из пяти доступных роторов. Быстрый ротор вращается на 1/26 поворота при каждом символе, введенном с помощью клавиатуры. Средний ротор делает 1/26 поворота при каждом полном повороте быстрого ротора. Медленный ротор делает 1/26 поворота для каждого законченного поворота среднего ротора.
- Отражатель, который является постоянным и предварительно замонтированным.
Кодовая книга — справочник шифров
Чтобы использовать "Энигму", была издана кодовая книга, которая в течение каждого дня дает несколько параметров настройки, включая:
a. три ротора, которые должны быть выбраны из пяти доступных;
b. порядок, в котором эти роторы должны быть установлены;
c. параметры установок для коммутационной панели;
d. код с тремя буквами дня.







