Модульная арифметика

Теория делимости

Теперь кратко обсудим теорию делимости — тема, с которой мы часто сталкиваемся в криптографии. Если a не равно нулю, а r = 0, в равенстве деления мы имеем

Мы тогда говорим, что a делится на n (или n — делитель a ). Мы можем также сказать, что a делится без остатка на n. Когда мы не интересуемся значением q, мы можем записать вышеупомянутые отношения как n|a. Если остаток не является нулевым, то n не делит, и мы можем записать отношения как n†a.

Пример 2.4

a. Целое число 4 делит целое число 32, потому что 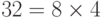. Это можно отобразить как 4|32. Число 8 не делит число 42, потому что 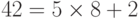. В этом уравнении число 2 — остаток. Это можно отобразить как 8†42.

Пример 2.5

а. Отображение делимости 13|78, 7|98, –6|24, 4|44, и 11 | (–33).

б. Отображение неделимости 13†27, 7†50, – 6†23, 4†41, и 11†(–32).

Свойства

Следующие несколько свойств теории делимости. Доказательства заинтересованный читатель может проверить в приложении Q.

Пример 2.6

а. Если 3|15 и 15|45 то, согласно третьему свойству, 3|45.

б. Если 3|15 и 3|9, то, согласно четвертому свойству, 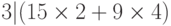, что означает 3|66.

Все делители

Положительное целое число может иметь больше чем один делитель. Например, целое число 32 имеет шесть делителей: 1, 2, 4, 8, 16 и 32. Мы можем упомянуть два интересных свойства делителей положительных целых чисел.

Наибольший общий делитель

Одно целое число, часто необходимое в криптографии, — наибольший общий делитель двух положительных целых чисел. Два положительных целых числа могут иметь много общих делителей, но только один наибольший общий делитель. Например, общие делители чисел 12 и 140 есть 1, 2 и 4. Однако наибольший общий делитель — 4 (см. рис. 2.6).

Рис. 2.6. Общие делители двух целых чисел

Алгоритм Евклида

Нахождение наибольшего общего делителя (НОД) двух положительных целых чисел путем составления списка всех общих делителей непригодно для достаточно больших чисел.

К счастью, больше чем 2000 лет назад математик по имени Эвклид разработал алгоритм, который может найти наибольший общий делитель двух положительных целых чисел. Алгоритм Евклида основан на следующих двух фактах (доказательство см. в приложении Q):

Первый факт говорит, что если второе целое число — 0, наибольший общий делитель равен первому числу. Второй факт позволяет нам изменять значение a на b, пока b не станет 0. Например, вычисляя НОД (36, 10), мы можем использовать второй факт несколько раз и один раз первый факт, как показано ниже.

НОД(36,10) = НОД(10,6) = НОД(6,4) = НОД(4,2) = НОД(2,0)

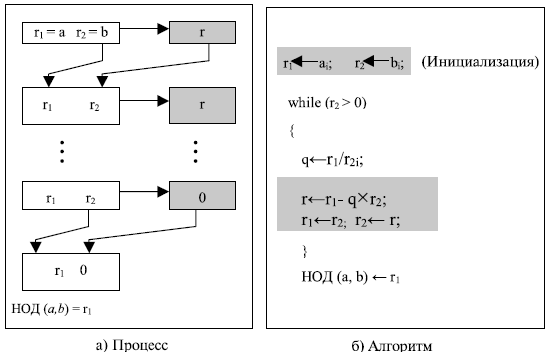
Другими словами, НОД (36, 10) = 2, НОД (10, 6) = 2, и так далее. Это означает, что вместо вычисления НОД (36, 10) мы можем найти НОД (2, 0). Рисунок 2.7 показывает, как мы используем вышеупомянутые два факта, чтобы вычислить НОД (a, b).

Рис. 2.7. Алгоритм Евклида

Для определения НОД мы используем две переменные, r₁ и r₂, чтобы запоминать изменяющиеся значения в течение всего процесса. Они имеют начальное значение a и b. На каждом шаге мы вычисляем остаток от деления r₁ на r₂ и храним результат в виде переменной r. Потом заменяем r₁, на r₂ и r₂ на r и продолжаем шаги, пока r не станет равным 0. В этот момент процесс останавливается и НОД (a, b) равен r₁.

Пример 2.7

Нужно найти наибольший общий делитель 2740 и 1760.

Решение

Применим вышеупомянутую процедуру, используя таблицу. Мы присваиваем начальное значение r₁ 2740 и r₂ значение 1760. В таблице также показаны значения q на каждом шаге. Мы имеем НОД (2740, 1760) = 20.

Пример 2.8

Найти наибольший общий делитель 25 и 60.

Решение

Мы выбрали этот конкретный пример, чтобы показать, что для алгоритма Евклида безразлично, если первое число меньше, чем второе. Все равно мы получаем правильный ответ НОД (25, 60) = 5.