|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Описание неопределенностей в теории принятия решений
Нечеткие множества как проекции случайных множеств. С самого начала появления современной теории нечеткости в 1960-е годы началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает распределение вероятностей. Отличие только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений несчетно) всегда равна 1, а сумма  значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на
значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на  (при
(при 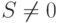 ), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого "примитивного сведения", поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согласовать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств
), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого "примитивного сведения", поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согласовать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств  и
и  . Как при этом преобразуются функции принадлежности
. Как при этом преобразуются функции принадлежности 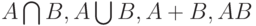 ? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними, причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.
? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними, причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.
В работах по нечетким множествам довольно часто утверждалось, что теория нечеткости является самостоятельным разделом прикладной математики и не имеет отношения к теории вероятностей. Авторы, сравнивавшие теорию нечеткости и теорию вероятностей, обычно подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сравнивают аксиоматику и сравнивают области приложений. Надо сразу отметить, что аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: "Арифметика применима тогда, когда она применима".
При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике. Напомним, что эти две аксиоматики - евклидовой геометрии и арифметики - на первый взгляд весьма сильно различаются.
Можно понять желание энтузиастов нового направления подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи нового подхода с ранее известными.
Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств. Еще в 1970-х годах было показано, что нечеткие множества естественно рассматривать как "проекции" случайных множеств. Рассмотрим основную идею этого метода сведения теории нечетких множеств к теории случайных множеств.
Определение 2. Пусть 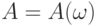 - случайное подмножество конечного множества У. Нечеткое множество В, определенное на
- случайное подмножество конечного множества У. Нечеткое множество В, определенное на 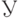 , называется проекцией
, называется проекцией  и обозначается Proj A, если
и обозначается Proj A, если
 |
( 11) |
при всех 
Очевидно, каждому случайному множеству А можно поставить в соответствие с помощью формулы (11) его проекцию - нечеткое множество В = Proj A. Оказывается, верно и обратное - любое нечеткое множество является проекцией некоторого случайного.
Цель сведения теории нечетких множеств к теории случайных множеств состоит в том, чтобы за любой конструкцией из нечетких множеств увидеть конструкцию из случайных множеств, определяющую свойства первой, аналогично тому, как за плотностью распределения вероятностей мы видим случайную величину. Сведение теории нечетких множеств к теории случайных теорем реализовано в виде системы теорем.
Методологические, теоретические и прикладные вопросы теории нечеткости обсуждаются в многочисленных литературных источниках.
Контрольные вопросы и задачи
- Расскажите о понятиях случайного события и его вероятности.
- Чем многомерный статистический анализ отличается от статистики объектов нечисловой природы?
- Покажите на примерах, что в задачах принятия решений исходные данные часто имеют интервальный характер.
- В чем особенности подхода статистики интервальных данных в задачах оценивания параметров?
-
Выполните операции над интервальными числами:
а)
![[1,2]+[3,4]](/sites/default/files/tex_cache/705bb46d7ec3dad5a48f56bd9557ddae.png) , б)
, б) ![[4,5]-[2,3]](/sites/default/files/tex_cache/b6f9317330737ce972dc44210d71f895.png) , в)
, в) ![[3,4]\times[5,7]](/sites/default/files/tex_cache/6aa69fe207a7ba5953461fb68b41b712.png) , г)
, г) ![[10,20]:[4,5]](/sites/default/files/tex_cache/3899fbac7da0c091529ae7b5f3f37e31.png) ;
;д)
![[0,2]+[3,5]](/sites/default/files/tex_cache/3e85513cf880c95c6376c90578a14a11.png) , е)
, е) ![[3,5]-[2,4]](/sites/default/files/tex_cache/d8dbcdb3dbed7316841533568efa403f.png) , ж)
, ж) ![[2,4]\times[5,8]](/sites/default/files/tex_cache/b7d428fe47be2d72d9c5ce46f8cb318c.png) , з)
, з) ![[15,25]:[1,5]](/sites/default/files/tex_cache/2dde7397404a1afd15012f424086b645.png) .
. -
Выпишите формулу для асимптотической нотны (ошибки по абсолютной величине не превосходят константы t, предполагающейся малой) для функции
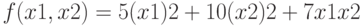
Вычислите асимптотическую нотну в точке
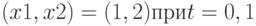 . Проделайте то же для функции
. Проделайте то же для функции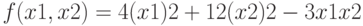
Вычислите асимптотическую нотну в точке
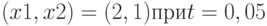 .
. - В каких случаях целесообразно применение нечетких множеств?
- Справедливо ли для нечетких множеств равенство
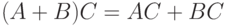 ? А равенство
? А равенство 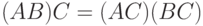 ?
? - Опишите с помощью нечеткого подмножества временной шкалы понятие "молодой человек".
- Опишите с помощью теории нечеткости понятие "куча зерен".
- Как можно проводить кластерный анализ совокупности нечетких множеств?
Темы докладов, рефератов, исследовательских работ
- Описание данных с помощью гистограмм и непараметрических оценок плотности.
- Сравнительный анализ методов оценивания параметров и характеристик.
- Преимущества одношаговых оценок по сравнению с оценками метода максимального правдоподобия.
- Методы проверки однородности для независимых и связанных выборок.
- Непараметрический регрессионный анализ.
- Структура статистики нечисловых данных.
- Аксиоматическое введение метрик и их использование в статистике объектов нечисловой природы.
- Законы больших чисел в пространствах произвольной природы.
- Непараметрические оценки плотности в пространствах произвольной природы, в том числе в дискретных пространствах.
- Оптимизационные постановки в вероятностно-статистических задачах принятия решений.
- Основные идеи статистики интервальных данных.
- Классическая математическая статистика как предельный случай статистики интервальных данных.
- Концепция рационального объема выборки.
- Сравнение методов оценивания параметров и характеристик распределений в статистике интервальных данных и в классической математической статистике.
- Подход к проверке гипотез в статистике интервальных данных.
- Метод наименьших квадратов для интервальных данных.
- Различные способы учета погрешностей исходных данных в статистических процедурах.
- Статистика интервальных данных как часть теории устойчивости (с использованием монографии [3]).
- Обсудите суждение: "Мы мыслим нечетко". Почему нечеткость мышления помогает взаимопониманию?
- Взаимосвязь теории нечеткости и теории вероятностей.
- Методы оценивания функции принадлежности.
- Теория нечеткости и интервальная математика.
- Описание данных для выборок, элементы которых - нечеткие множества.
- Регрессионный анализ нечетких переменных.
- Непараметрические оценки плотности распределения вероятностей в пространстве нечетких множеств.

