|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Конкретные направления менеджмента
Модель оптимизации моментов выпуска продукции на рынок. Рассмотрим эскизную математическую модель, позволяющую рассчитать оптимальные моменты выпуска на рынок новых моделей продукции. Рис.6.1 позволяет сравнить динамику мирового уровня качества и уровня качества продукции конкретного предприятия. Мировой уровень качества непрерывно растет, в то время как уровень качества продукции конкретного предприятия меняется скачкообразно. Он заметно увеличивается при выпуске на рынок новой марки продукции, а затем остается постоянным вплоть до выпуска следующей марки. В течение жизненного цикла очередной марки продукции ее уровень качества сначала заметно выше мирового, затем преимущество уменьшается, наконец, уровень качества оказывается ниже мирового, и через некоторое время марка снимается с производства.

Рис. 6.1. Сравнение динамики мирового уровня качества и уровня качества продукции конкретного предприятия
В какие оптимальные моменты  выпускать на рынок новые марки продукции? Чтобы ответить на этот вопрос, необходимо сформировать функционал, который будем оптимизировать, выбирая моменты
выпускать на рынок новые марки продукции? Чтобы ответить на этот вопрос, необходимо сформировать функционал, который будем оптимизировать, выбирая моменты 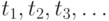
Предположим, что изменение во времени мирового уровня качества рассматриваемой продукции  можно описать линейной функцией:
можно описать линейной функцией:

В качестве модели рынка примем модель чистой (совершенной) конкуренции. В соответствии с ней вклад конкретного предприятия в объем мирового рынка бесконечно мал, а цены определяются мировым уровнем качества. Можно сказать, что мировой уровень качества является оптимальным. Самым лучшим для предприятия был бы выпуск продукции на этом уровне. К сожалению, это невозможно по технологическим причинам. Пусть  - стоимость осуществления скачка, т.е. разработки и подготовки к производству очередной марки (модификации) продукции. Примем для простоты, что стоимости скачков любой величины одинаковы.
- стоимость осуществления скачка, т.е. разработки и подготовки к производству очередной марки (модификации) продукции. Примем для простоты, что стоимости скачков любой величины одинаковы.
Следовательно, превышение мирового уровня не приносит предприятию дополнительного дохода. Поэтому предположим, что дополнительные затраты на превышение уровня качества  выпускаемой продукции сверх мирового уровня пропорциональны этому превышению, т.е. за время
выпускаемой продукции сверх мирового уровня пропорциональны этому превышению, т.е. за время 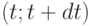 равны
равны
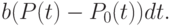
где  - коэффициент пропорциональности и
- коэффициент пропорциональности и 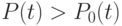 .
.
При отставании уровня качества продукции от мирового предприятие несет заметные убытки, в частности, ему приходится снижать цены. Пусть потери от морального старения продукции пропорциональны отставанию от мирового уровня качества, т.е. за время 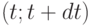 равны
равны
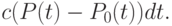
где  - коэффициент пропорциональности и
- коэффициент пропорциональности и 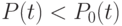 .
.
Функционал, который будем оптимизировать, выбирая моменты 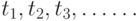 и соответствующие величины скачков, равен сумме расходов на запуск новых марок, затрат на превышение уровня качества
и соответствующие величины скачков, равен сумме расходов на запуск новых марок, затрат на превышение уровня качества  выпускаемой продукции сверх мирового и потерь от морального старения продукции ввиду отставания от мирового уровня качества. Пусть за время
выпускаемой продукции сверх мирового и потерь от морального старения продукции ввиду отставания от мирового уровня качества. Пусть за время 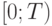 выпущено на рынок
выпущено на рынок 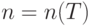 новых марок. Тогда функционал имеет вид
новых марок. Тогда функционал имеет вид
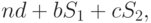
где  - суммарная площадь треугольников, образованных графиками
- суммарная площадь треугольников, образованных графиками  и
и  и расположенных выше прямой
и расположенных выше прямой  - суммарная площадь треугольников, образованных графиками
- суммарная площадь треугольников, образованных графиками  и
и 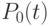 и расположенных ниже прямой
и расположенных ниже прямой  .
.
Минимизацию затрат проведем в три этапа. На первом этапе зафиксируем моменты 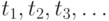 Рассмотрим два соседних момента
Рассмотрим два соседних момента 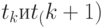 . Положим
. Положим 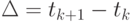 . Тогда ситуация полностью описана, если задан промежуток времени
. Тогда ситуация полностью описана, если задан промежуток времени  такой, что в момент
такой, что в момент  уровень качества выпускаемой предприятием продукции совпадает с мировым уровнем качества (рис.6.2).
уровень качества выпускаемой предприятием продукции совпадает с мировым уровнем качества (рис.6.2).
Меняя величину  , мы изменяем высоту рассматриваемой "ступеньки" графика
, мы изменяем высоту рассматриваемой "ступеньки" графика  , не влияя на остальные "ступеньки". В результате можно провести локальную оптимизацию высоты "ступенек" при заданных моментах
, не влияя на остальные "ступеньки". В результате можно провести локальную оптимизацию высоты "ступенек" при заданных моментах 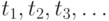 выпуска на рынок очередных марок. Задача локальной оптимизации допускает декомпозицию, т.е. разбивается на задачи оптимизации для каждой ступеньки по отдельности.
выпуска на рынок очередных марок. Задача локальной оптимизации допускает декомпозицию, т.е. разбивается на задачи оптимизации для каждой ступеньки по отдельности.
За промежуток времени  затраты, связанные с превышением уровня качества сверх мирового, как видно из рис.6.2, равны
затраты, связанные с превышением уровня качества сверх мирового, как видно из рис.6.2, равны
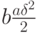
а потери из-за морального старения (при отставании от мирового уровня) равны
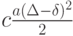
Следовательно, суммарные потери за рассматриваемый интервал времени момента 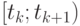 равны
равны
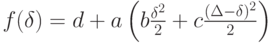
Выбирая  оптимальным образом, минимизируем суммарные затраты и потери за рассматриваемый интервал времени. Продифференцировав функцию
оптимальным образом, минимизируем суммарные затраты и потери за рассматриваемый интервал времени. Продифференцировав функцию  по
по  и приравняв производную 0, получим оптимальное значение
и приравняв производную 0, получим оптимальное значение  , а именно:
, а именно:

При оптимальном  затраты за период с
затраты за период с  до
до  , как нетрудно подсчитать, равны
, как нетрудно подсчитать, равны
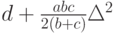
На втором этапе оптимизации зафиксируем число скачков и найдем при этом условии оптимальные моменты скачков  Положим
Положим 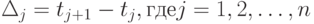 , причем примем
, причем примем 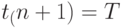 , где T - горизонт планирования. Тогда суммарные затраты за весь рассматриваемый интервал планирования равны
, где T - горизонт планирования. Тогда суммарные затраты за весь рассматриваемый интервал планирования равны

Эту функцию необходимо минимизировать по всем  неотрицательным переменным
неотрицательным переменным 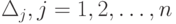 , при условии
, при условии
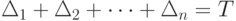
Достаточно решить чисто математическую задачу оптимизации
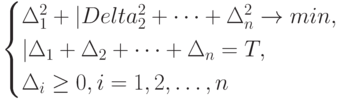
где 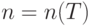 . Для ее решения целесообразно ввести новые переменные
. Для ее решения целесообразно ввести новые переменные 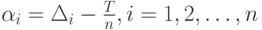 Тогда
Тогда
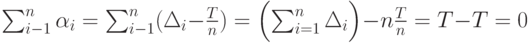
Поскольку 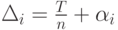 то
то  следовательно, с учетом предыдущего равенства имеем
следовательно, с учетом предыдущего равенства имеем
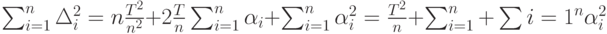
Сумма квадратов всегда неотрицательна. Она достигает минимума, равного 0, когда все переменные равны 0, т.е. при  Тогда
Тогда
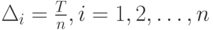
При этих значениях  выполнены все ограничения оптимизационной задачи.
выполнены все ограничения оптимизационной задачи.
Итак, интервалы между скачками должны иметь одинаковую длину. При фиксированном числе скачков n минимальное значение суммарных затрат равно
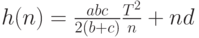
На третьем этапе оптимизации надо найти оптимальное число скачков n, или, что эквивалентно, интервал между скачками  .
.
Как следует из последней формулы, суммарные удельные затраты, приходящиеся на одну единицу времени, имеют вид
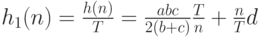
Эту функцию легче минимизировать, если перейти к переменной  , где
, где 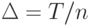 . Удельные затраты равны
. Удельные затраты равны

Минимизируем эту функцию по  . Дифференцируя по
. Дифференцируя по  и приравнивая производную 0, получаем, что оптимальный интервал между скачками имеет длину
и приравнивая производную 0, получаем, что оптимальный интервал между скачками имеет длину
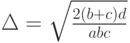
Полученная формула позволяет делать как количественные, так и качественные выводы. Например, если мировой уровень качества практически не меняется (т.е.  ), то интервал между выпуском новых марок очень большой (т.е.
), то интервал между выпуском новых марок очень большой (т.е. 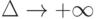 ). Полученная формула напоминает формулу Вильсона (в других источниках - формула квадратного корня) в теории управления запасами - части логистики.
). Полученная формула напоминает формулу Вильсона (в других источниках - формула квадратного корня) в теории управления запасами - части логистики.
Отметим, что проведенные на третьем этапе рассуждения не вполне корректны. Минимизация проводилась по всем положительным  , а на самом деле
, а на самом деле  должно лежать в дискретном множестве
должно лежать в дискретном множестве  Поэтому оптимальное
Поэтому оптимальное  - одно из значений
- одно из значений 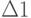 и
и 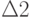 , где
, где



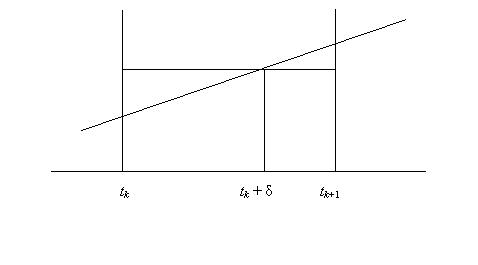
 меньше.
меньше.