|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Управление инвестиционными проектами
Дисконт-функция
Рассмотрим основные для дальнейшего понятия дисконт-функции и нормы дисконта. (Термины используем в соответствии с отраженной в монографии традицией.)
Важно с самого начала осознать, что 1 руб. сейчас и 1 руб. через год - это совсем разные экономические величины. Дисконт-функция как функция от времени как раз и показывает, сколько стоит 1 рубль в заданный момент времени, если его привести к начальному моменту. Например, "инфляционная" дисконт-функция на 1 сентября 2002 г. равна 1/50, поскольку индекс инфляции на этот момент равен 50 (округленно), если в качестве начального момента принять март 1991 г. Индекс инфляции рассчитан по независимо собранным данным в Институте высоких статистических технологий и эконометрики МГТУ им. Н.Э.Баумана. При этом индекс инфляции показывает сравнительную покупательную способность рубля - на 50 руб. сентября 2002 г. можно купить (в среднем) столько же, сколько на 1 рубль в марте 1991 г.
В то же время "банковская" дисконт-функция учитывает упущенную выгоду. Если бы 1 рубль был вложен в банк с фиксированной процентной ставкой в неизменных ценах, равной, например, 10% годовых, то за 10,5 лет (1 марта 1991 г. - 1 сентября 2002 г.) он превратился бы в 2,72 руб. в неизменных ценах (марта 1991 г.). Т.е., с учетом инфляции, в 136 руб. сентября 2002 г. Отметим, что, строго говоря, реальная дисконт-функция, как и индекс инфляции, является функцией двух аргументов - начального и текущего моментов времени.
Очевидно, в определении дисконт-функции есть неопределенность, по крайней мере такая же, как в определении индекса инфляции, для которого неопределенность связана с возможностью выбора той или иной потребительской корзины. "Естественная" потребительская корзина для данного региона или инвестиционного проекта может отличаться от таковой для экономики в целом и для товаров народного потребления в частности, поскольку завод потребляет иные виды материальных ценностей, чем человек. Есть зависимость от использования тех или иных цен в реально имеющемся диапазоне, а также зависит от степени заинтересованности организации, рассчитывающей индекс.
Подведем итоги. Дисконт-функцию можно разложить на две составляющие - общую для экономики в целом и специфическую для данной отрасли или данного инвестиционного проекта. Если дисконт-функция - константа для разных отраслей, товаров и проектов, то эта константа называется дисконт-фактором, или просто дисконтом.
Общая (для экономики в целом) дисконт-функция определяется совместным действием реальной процентной ставки и индекса инфляции. Реальная процентная ставка описывает "нормальный" рост экономики (т.е. без учета инфляции). В стабильной ситуации (при "долговременном конкурентном равновесии"), как известно из экономической теории, доходность от вложения средств в различные отрасли, в частности, в банковские депозиты, должна быть примерно одинакова. В современных условиях эта величина (норма рентабельности) равна примерно 6-12%. Примем для определенности максимальное значение, равное 12%. Другими словами, 1 рубль через год превращается в 1,12 руб., а потому 1 рубль через год соответствует  руб. сейчас. Из-за инфляции нынешний 1 руб. через год превращается в большую величину, чем 1,12 руб. Поэтому 0,89 - это максимально возможное в современных условиях значение дисконта.
руб. сейчас. Из-за инфляции нынешний 1 руб. через год превращается в большую величину, чем 1,12 руб. Поэтому 0,89 - это максимально возможное в современных условиях значение дисконта.
Обозначим дисконт буквой С. Как установлено выше,  - число между 0 и 1, точнее, максимально возможное значение дисконта равно 0,89. В общем случае, если
- число между 0 и 1, точнее, максимально возможное значение дисконта равно 0,89. В общем случае, если  - банковский процент (плата за депозит), т.е. вложив в начале года в банк 1 руб., в конце года получим
- банковский процент (плата за депозит), т.е. вложив в начале года в банк 1 руб., в конце года получим  руб., то дисконт определяется по формуле
руб., то дисконт определяется по формуле
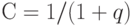 |
( 1) |
Отметим, что при таком подходе полагают, что банковские проценты платы за депозит одинаковы во всех банках. Более правильно было бы считать q, а потому и С, нечисловыми величинами, а именно, интервалами ![[q_1 , q_2]](/sites/default/files/tex_cache/e82dba2c68d23384ca832e3b3aa2ee17.png) и
и ![[С_1 , С_2]](/sites/default/files/tex_cache/39502377bd3514886d4a2b2d91d9e129.png) соответственно. При этом связь между интервалами определяется в соответствии с формулой (1), а именно:
соответственно. При этом связь между интервалами определяется в соответствии с формулой (1), а именно:
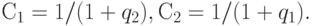
Следовательно, выводы, полученные с помощью рассматриваемых величин, должны быть исследованы на устойчивость (в инженерной среде принят также термин "чувствительность") по отношению к отклонениям этих величин в пределах заданных интервалов.
Как функцию времени t дисконт-функцию обозначим 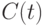 .Тогда при постоянстве дисконт-фактора во времени дисконт-функция имеет вид
.Тогда при постоянстве дисконт-фактора во времени дисконт-функция имеет вид
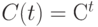 |
( 2) |
т.е. С возводится в степень t, дисконт-функция является показательной функцией. Согласно формуле (2) через 2 года 1 руб. превращается в 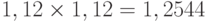 , через 3 - в 1,4049, следовательно, 1 руб., полученный через 2 года, соответствует 79,72 копейки сейчас, а 1 руб., обещанный через 3 года, соответствует 0,71 руб. сейчас. Другими словами,
, через 3 - в 1,4049, следовательно, 1 руб., полученный через 2 года, соответствует 79,72 копейки сейчас, а 1 руб., обещанный через 3 года, соответствует 0,71 руб. сейчас. Другими словами, 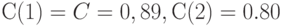 (с точностью до двух знаков после запятой), а
(с точностью до двух знаков после запятой), а  .
.
Если дисконт-фактор меняется год от году, в первый год равен  , во второй год -
, во второй год - 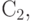 в третий год -
в третий год - 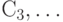 , в t-ый год -
, в t-ый год -  то в этом общем случае дисконт-функция имеет вид
то в этом общем случае дисконт-функция имеет вид
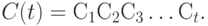 |
( 3) |
Пусть, например,  , тогда согласно формуле (3) имеем
, тогда согласно формуле (3) имеем 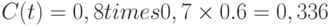 . Если
. Если 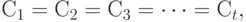 то формула (3) переходит в формулу (2).
то формула (3) переходит в формулу (2).
Индекс инфляции  (в разах, а не в процентах) за год соответствует дисконту
(в разах, а не в процентах) за год соответствует дисконту 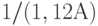 , т.е. 1 руб. сейчас соответствует
, т.е. 1 руб. сейчас соответствует 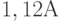 руб. через год. Долговременная динамика индекса инфляции плохо предсказуема.
руб. через год. Долговременная динамика индекса инфляции плохо предсказуема.
Частная дисконт-функция зависит от динамики цен и темпов технологического обновления (физического износа, морального старения, научно-технического прогресса) в отрасли. Так, вложения в компьютеры обесцениваются гораздо быстрее, чем вложения в недвижимость (здания, землю) - для покупки недвижимости, которая сейчас стоит 1 руб., через год может понадобиться 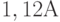 руб., а для покупки компьютера, который сейчас стоит 1 руб., может понадобиться через год лишь 0,8 руб. (в ценах, которые будут через год). Строго говоря, частная дисконт-функция - своя для каждой организации, соответствующая набору товаров и услуг, положению на финансовом рынке, специфическим именно для этой организации.
руб., а для покупки компьютера, который сейчас стоит 1 руб., может понадобиться через год лишь 0,8 руб. (в ценах, которые будут через год). Строго говоря, частная дисконт-функция - своя для каждой организации, соответствующая набору товаров и услуг, положению на финансовом рынке, специфическим именно для этой организации.
Характеристики финансовых потоков
В основе процесса принятия управленческих решений инвестиционного характера лежит оценка и сравнение объема предполагаемых инвестиций и будущих денежных поступлений. Общая логика анализа с использованием формализованных критериев в принципе достаточно очевидна - необходимо сравнивать величину требуемых инвестиций с прогнозируемыми доходами.
Как уже говорилось, инвестиционные проекты, результаты применения управляющих воздействий к процессам налогообложения и другие экономические реалии описываются финансовыми потоками (потоками платежей и поступлений), т.е. функциями (временными рядами), а сравнивать функции естественно с помощью тех или иных характеристик (критериев).
Критерии (показатели, характеристики финансовых потоков), используемые при анализе инвестиционной деятельности, можно подразделить на две группы в зависимости от того, учитывается или нет временной параметр: а) основанные на дисконтированных оценках; б) основанные на учетных (номинальных) оценках. К первой группе относятся критерии:
чистая текущая стоимость (Net Present Value, NPV) ;
индекс рентабельности инвестиции (Profitability Index, PI) ;
внутренняя норма доходности (Internal Rate of Return, IRR) ;
модифицированная внутренняя норма доходности (Modified Internal Rate of Return, MIRR) ;
дисконтированный срок окупаемости инвестиции (Discounted Payback Period, DPP).
Ко второй группе относятся:
срок окупаемости инвестиции (Payback Period, PP) ;
коэффициент эффективности инвестиции (Accounting Rate of Return, ARR).
Чистая текущая стоимость. Этот критерий основан на сопоставлении величины исходных инвестиций 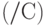 с общей суммой дисконтированных чистых денежных поступлений, генерируемых проектом в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента q, устанавливаемого аналитиком (выступающим от имени инвестора) самостоятельно исходя из ежегодного процента возврата, который инвестор хочет или может иметь на инвестируемый им капитал.
с общей суммой дисконтированных чистых денежных поступлений, генерируемых проектом в течение прогнозируемого срока. Поскольку приток денежных средств распределен во времени, он дисконтируется с помощью коэффициента q, устанавливаемого аналитиком (выступающим от имени инвестора) самостоятельно исходя из ежегодного процента возврата, который инвестор хочет или может иметь на инвестируемый им капитал.
Допустим, делается прогноз, что исходные инвестиции 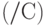 будут генерировать в течение n лет годовые доходы в размере
будут генерировать в течение n лет годовые доходы в размере  . Общая накопленная величина дисконтированных доходов (Present Value, PV) и чистая текущая стоимость (Net Present Value, NPV) соответственно рассчитываются по формулам:
. Общая накопленная величина дисконтированных доходов (Present Value, PV) и чистая текущая стоимость (Net Present Value, NPV) соответственно рассчитываются по формулам:
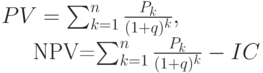
Очевидно, что если:
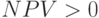 , то проект следует принять;
, то проект следует принять;
 , то проект следует отвергнуть;
, то проект следует отвергнуть;
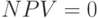 , то проект ни прибыльный, ни убыточный.
, то проект ни прибыльный, ни убыточный.
Теперь дадим экономическую интерпретацию значению критерия 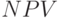 с позиции владельцев компании:
с позиции владельцев компании:
- если
 , то в случае принятия проекта ценность компании уменьшится, т.е. владельцы компании понесут убыток;
, то в случае принятия проекта ценность компании уменьшится, т.е. владельцы компании понесут убыток; - если
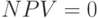 , то в случае принятия проекта ценность компании не изменится, т.е.благосостояние ее владельцев останется на прежнем уровне;
, то в случае принятия проекта ценность компании не изменится, т.е.благосостояние ее владельцев останется на прежнем уровне; - если
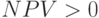 , то в случае принятия проекта ценность компании, а следовательно, и благосостояние ее владельцев увеличатся.
, то в случае принятия проекта ценность компании, а следовательно, и благосостояние ее владельцев увеличатся.
При прогнозировании доходов по годам необходимо по возможности учитывать все виды поступлений как производственного, так и непроизводственного характера, которые могут быть ассоциированы с данным проектом. Так, если по окончании периода реализации проекта планируется поступление средств в виде ликвидационной стоимости оборудования или высвобождения части оборотных средств, они должны быть учтены как доходы соответствующих периодов.
Если проект предполагает не разовую инвестицию, а последовательное инвестирование финансовых ресурсов в течение  лет, то формула для расчета
лет, то формула для расчета 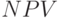 модифицируется следующим образом:
модифицируется следующим образом:
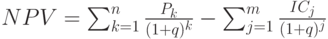
где 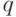 - дисконт-фактор.
- дисконт-фактор.
Необходимо отметить, что показатель 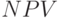 отражает прогнозную оценку изменения экономического потенциала организации в случае принятия рассматриваемого проекта. Этот показатель аддитивен в пространственно-временном аспекте, т.е.
отражает прогнозную оценку изменения экономического потенциала организации в случае принятия рассматриваемого проекта. Этот показатель аддитивен в пространственно-временном аспекте, т.е. 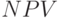 различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
различных проектов можно суммировать. Это очень важное свойство, выделяющее этот критерий из всех остальных и позволяющее использовать его в качестве основного при анализе оптимальности инвестиционного портфеля.
Как уже отмечалось, не всегда инвестиции сводятся к одномоментному вложению капитала, а возврат происходит равными порциями. Чаще приходится анализировать поток платежей и поступлений общего вида. Будем в качестве потока платежей и поступлений рассматривать последовательность 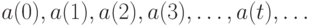 . Если величина
. Если величина 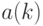 отрицательна, то это платеж, а если она положительна - поступление. Выше был рассмотрен важный частный случай - поток с одним платежом
отрицательна, то это платеж, а если она положительна - поступление. Выше был рассмотрен важный частный случай - поток с одним платежом 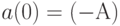 и дальнейшими поступлениями
и дальнейшими поступлениями  .
.
Чистую текущую стоимость, или, как ее иногда называют, дисконтированную прибыль, чистый приведенный доход (или эффект, или величину, по-английски - Net Present Value, сокращенно NPV ), т.е. разность между дисконтированными доходами и расходами, рассчитывают для потока платежей путем приведения затрат и поступлений к одному моменту времени:
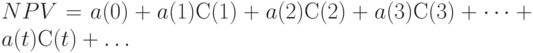 |
( 4) |
где 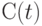 - дисконт-функция, определяемая по формулам (2) или (3). В простейшем случае, когда дисконт-фактор не меняется год от года и согласно формуле (1) имеет вид
- дисконт-функция, определяемая по формулам (2) или (3). В простейшем случае, когда дисконт-фактор не меняется год от года и согласно формуле (1) имеет вид 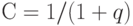 , где
, где 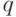 - банковский процент, формула для чистой текущей стоимости конкретизируется:
- банковский процент, формула для чистой текущей стоимости конкретизируется:
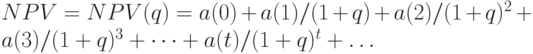 |
( 5) |
Пусть, например, 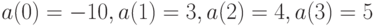 . Пусть
. Пусть 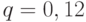 , тогда, как установлено выше, согласно формуле (2) значения дисконт-функции таковы:
, тогда, как установлено выше, согласно формуле (2) значения дисконт-функции таковы: 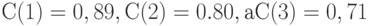 . Тогда согласно формуле (4)
. Тогда согласно формуле (4)
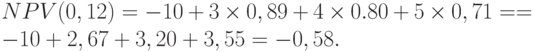
Таким образом, этот проект является невыгодным для вложения капитала, поскольку 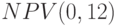 отрицательно, в то время как при отсутствии дисконтирования (т.е. при
отрицательно, в то время как при отсутствии дисконтирования (т.е. при 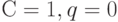 ) вывод иной:
) вывод иной:

Таким образом, важной проблемой является выбор дисконт-функции. В качестве приближения обычно используют постоянное дисконтирование, хотя экономическая история последних лет показывает, что банки часто меняют проценты платы за депозит, так что формула (3) для дисконт-функции с различными процентами в разные годы более реалистична, чем формула (2).
Часто предлагают использовать норму дисконта, равную приемлемой для инвестора норме дохода на капитал. Это предложение означает, что экономисты явным образом обращаются к инвестору как к эксперту, который должен назвать им некоторое число исходя из своего опыта и интуиции. Кроме того, при этом игнорируется изменение указанной нормы во времени.

