Методы классификации и прогнозирования. Метод опорных векторов. Метод "ближайшего соседа". Байесовская классификация
Линейный SVM
Решение задачи бинарной классификации при помощи метода опорных векторов заключается в поиске некоторой линейной функции, которая правильно разделяет набор данных на два класса. Рассмотрим задачу классификации, где число классов равно двум.
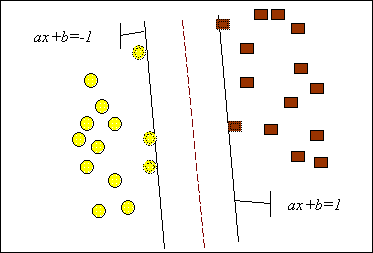
Задачу можно сформулировать как поиск функции f(x), принимающей значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. В качестве исходных данных для решения поставленной задачи, т.е. поиска классифицирующей функции f(x), дан тренировочный набор векторов пространства, для которых известна их принадлежность к одному из классов. Семейство классифицирующих функций можно описать через функцию f(x). Гиперплоскость определена вектором а и значением b, т.е. f(x)=ax+b. Решение данной задачи проиллюстрировано на рис. 10.4.
В результате решения задачи, т.е. построения SVM-модели, найдена функция, принимающая значения меньше нуля для векторов одного класса и больше нуля - для векторов другого класса. Для каждого нового объекта отрицательное или положительное значение определяет принадлежность объекта к одному из классов.
Наилучшей функцией классификации является функция, для которой ожидаемый риск минимален. Понятие ожидаемого риска в данном случае означает ожидаемый уровень ошибки классификации.
Напрямую оценить ожидаемый уровень ошибки построенной модели невозможно, это можно сделать при помощи понятия эмпирического риска. Однако следует учитывать, что минимизация последнего не всегда приводит к минимизации ожидаемого риска. Это обстоятельство следует помнить при работе с относительно небольшими наборами тренировочных данных.
Эмпирический риск - уровень ошибки классификации на тренировочном наборе.
Таким образом, в результате решения задачи методом опорных векторов для линейно разделяемых данных мы получаем функцию классификации, которая минимизирует верхнюю оценку ожидаемого риска.
Одной из проблем, связанных с решением задач классификации рассматриваемым методом, является то обстоятельство, что не всегда можно легко найти линейную границу между двумя классами.
В таких случаях один из вариантов - увеличение размерности, т.е. перенос данных из плоскости в трехмерное пространство, где возможно построить такую плоскость, которая идеально разделит множество образцов на два класса. Опорными векторами в этом случае будут служить объекты из обоих классов, являющиеся экстремальными.
Таким образом, при помощи добавления так называемого оператора ядра и дополнительных размерностей, находятся границы между классами в виде гиперплоскостей.
Однако следует помнить: сложность построения SVM-модели заключается в том, что чем выше размерность пространства, тем сложнее с ним работать. Один из вариантов работы с данными высокой размерности - это предварительное применение какого-либо метода понижения размерности данных для выявления наиболее существенных компонент, а затем использование метода опорных векторов.
Как и любой другой метод, метод SVM имеет свои сильные и слабые стороны, которые следует учитывать при выборе данного метода.
Недостаток метода состоит в том, что для классификации используется не все множество образцов, а лишь их небольшая часть, которая находится на границах.
Достоинство метода состоит в том, что для классификации методом опорных векторов, в отличие от большинства других методов, достаточно небольшого набора данных. При правильной работе модели, построенной на тестовом множестве, вполне возможно применение данного метода на реальных данных.