|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Криптографическая система RSA
Рекомендации
Следующие рекомендации основаны на теоретических и экспериментальных результатах.
- Число битов для n должно быть, по крайней мере, 1024. Это означает, что n должно быть приблизительно 21024, или 309 десятичных цифр.
- Два простых числа p и q должны каждый быть по крайней мере 512 битов. Это означает, что p и q должны быть приблизительно 2512 или 154 десятичными цифрами.
- Значения p и q не должен быть очень близки друг к другу.
- p – 1 и q – 1 должны иметь по крайней мере один большой простой сомножитель.
- Отношение p/q не должно быть близко к рациональному числу с маленьким числителем или знаменателем.
- Модуль n не должен использоваться совместно.
- Значение e должно быть 216 + 1 или целым числом, близким к этому значению.
- Если произошла утечка частного ключа d, Боб должен немедленно изменить n так же, как e и d. Было доказано, что знание n и одной пары (e, d) может привести к открытию других пар того же самого модуля.
- Сообщения должны быть дополнены, используя OAEP, который рассматривается далее.
Оптимальное асимметричное дополнение шифрования (OAEP — Optimal Assimetric Encryption Padding)
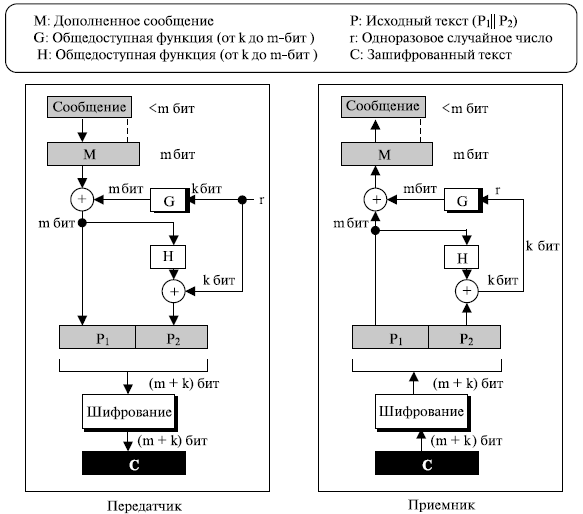
Как мы упоминали ранее, короткое сообщение в RSA делает зашифрованный текст уязвимым к атакам короткого сообщения. Там же показано, что простое добавление фиктивных данных (дополнение) к сообщению затрудняет работу Евы, но, приложив дополнительные усилия, она может все еще атаковать зашифрованный текст. Решение, предложенное группой RSA и некоторыми другими разработчиками, состоит в том, чтобы применить процедуру, названную оптимальным асимметричным дополнением шифрования (OAEP). Рисунок 14.9 показывает простую версию этой процедуры; реализация может использовать более сложную версию.
Идея, показанная на рисунке 14.9, — это то, что P = P1 || P2, где P1 — замаскированная версия дополненного сообщения, М; P2 передается, чтобы позволить Бобу найти маску.
Шифрование. Ниже показаны шаги процесса шифрования.
- Алиса дополняет сообщение, чтобы сделать его m -битовым. Мы обозначим его М.
- Алиса выбирает случайное число r из k бит. Обратите внимание, что r применяется только однажды и затем уничтожается.
- Алиса использует общедоступную одностороннюю функцию G, которая принимает целое r -битовое число, и создает m -разрядное целое число ( m — размера М, и r <m ). Это — маска.
- Алиса применяет маску, G (r), чтобы создать первую часть исходного текста
 является замаскированным сообщением.
является замаскированным сообщением. - Алиса создает вторую часть исходного текста
 . Функция H — другая общедоступная функция, которая принимает m -битовые входные сообщения и создает k -битовые выходные сообщения. Эта функция может быть криптографической хэш-функцией ю P2 используется для того, чтобы дать возможность Бобу снова создать маску после дешифрации.
. Функция H — другая общедоступная функция, которая принимает m -битовые входные сообщения и создает k -битовые выходные сообщения. Эта функция может быть криптографической хэш-функцией ю P2 используется для того, чтобы дать возможность Бобу снова создать маску после дешифрации. - Алиса создает C = Pe = (P1 || P2) e и передает C Бобу.
Дешифрование. Следующие шаги показывают процесс дешифрования:
- Боб создает P = Cd = (P1 || P2).
- Боб сначала обновляет значение r, используя
 .
. - Боб применяет
 , чтобы обновить значение дополненного сообщения.
, чтобы обновить значение дополненного сообщения. - После удаления дополнения М, Боб находит первоначальное сообщение.
Ошибка в передаче
Если хотя бы один бит в течение передачи принят с ошибкой, текст, зашифрованный RSA, будет принят неправильно. Если полученный зашифрованный текст отличается от переданного, приемник не может определить первоначальный исходный текст. Исходный текст, вычисленный на стороне приемника, может очень отличаться от передаваемого передатчиком. Среда передачи должна быть освобожденной от ошибок за счет добавления избыточных бит или обнаружения и исправления ошибки в зашифрованном тексте.
Пример 14.8
Вот — реальный пример. Мы выбираем 512 -битовые p и q, вычисляем n и  , затем выбираем e и испытываем, что оно взаимно простое с
, затем выбираем e и испытываем, что оно взаимно простое с  . Затем мы вычисляем d. Наконец, мы показываем результат шифрования и дешифрования. Целое число p — это число со 159 цифрами.
. Затем мы вычисляем d. Наконец, мы показываем результат шифрования и дешифрования. Целое число p — это число со 159 цифрами.
P = 961303453135835045741915812806154279093098455949962158225831508 796479404550564706384912571601803475031209866660649242019180878 0667421096063354219926661209
Целое число q содержит 160 цифр.
q = 12060191957231446918276794204450896001555925054637033936061 798321731482148483764659215389453209175225273226830107120695604 602513887145524969000359660045617
Модуль 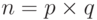 . Это число имеет 309 цифр.
. Это число имеет 309 цифр.
n = 1159350417396761496889250986461588752377145737545414477548552613 7614788540S32635081727687881596832516846884930062548576411125016 241455233918.292716250765677272746009708271412773043496050055634 7274566628060099924037102991424472292215772798531727033839381334 692684137 327622000966676671831831088373420823444370953
 имеет 309 цифр.
имеет 309 цифр.
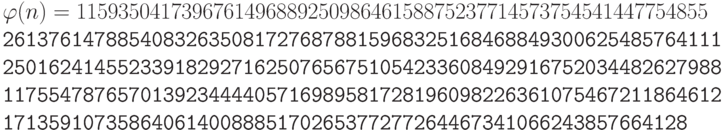
Боб выбирает e = 35535 (идеально 65537 ), и испытание на простое число показывает, что это число и  — взаимно простые числа. Затем Боб находит инверсию
— взаимно простые числа. Затем Боб находит инверсию 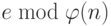 — это обозначается d.
— это обозначается d.
e = 35535 ________________________________________________________________ d = 58008302S6003776393609366128967791759466906208965096218042286 6111380593852S2235873170628691003002171085904433840217072986908 760061153062025249598844480475682409662470814858171304632406440 777048331340108509473852956450719367740611973265574242372176176 74620776371642 0760033708533328853214470885955136670294831
Алиса хочет передать сообщение "THIS IS TEST", которое может быть представлено числовыми значениями, используя схему кодирования 00-26 ( 26 — пробел).
P = 1907081826081826002619041819
Шифрованный текст, вычисленный Алисой, — это C = Pe, числовое значение приведено ниже.
С = 4753091236462268272063655506105451809423717960704917165232392 430544529606131993285666178434183591141511974112520056829797945 717360361012782188478927415660904800235071907152771859149751884 658886321011483541033616578984679683867637337657774656250792805 2114814184404814184430812773059004692874248559166462108656 Боб может восстановить из зашифрованного текста исходный
Боб может восстановить из зашифрованного текста исходный текст, используя P = Cd.
P = 1907081826081826002619041819
После расшифровки восстановленный исходный текст — "THIS IS TEST".
Приложения
Хотя RSA может использоваться, чтобы зашифровать и расшифровывать реальные сообщения, это — очень длинные сообщения для RSA. Поэтому он является полезным для коротких сообщений. В частности мы увидим, что RSA применяется в цифровых подписях и других криптографических системах, которые нужны для шифрования маленьких сообщений без доступа к симметрическому ключу. Как мы увидим в последующих лекциях, RSA также используется для установления подлинности документа.