НОУ ИНТУИТ | Математика криптографии и теория шифрования. Лекция 12: Простые числа

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: платный

|

Вам нравится? Нравится 71 студенту

| Поделиться |

Поддержать программу

12.3. Разложение на множители

Разложение на множители — предмет непрерывного исследования в прошлом; и такие же исследования, вероятно, продолжатся в будущем. Разложение на множители играет очень важную роль в безопасности некоторых криптосистем с открытым ключом (см. лекции 14-15).

Основная теорема арифметики

Согласно Основной теореме арифметики любое положительное целое число больше единицы может быть уникально записано в следующей главной форме разложения на множители, где p₁, p₂, ..., p_k — простые числа и e₁, e₂, ..., e_k — положительные целые числа.

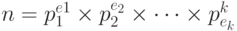
$n = p^{e1}_1\times p_{2}^{e_2}\times\dots\times p^{k}_{e_k}$

Есть непосредственные приложения разложения на множители, такие как вычисление наибольшего общего делителя и наименьшего общего множителя.

Наибольший общий делитель

В "Модульная арифметика" мы уже обсуждали наибольший общий делитель двух номеров, НОД (a, b). Посмотрите, как евклидов алгоритм дает это значение, но это значение может также быть найдено, если мы знаем разложение на множители чисел a и b.

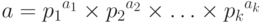
$a = {p_1}^{{a_1}} \times {p_2}^{{a_2}} \times \ldots \times {p_k}^{{a_k}}$

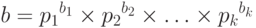
$b = {p_1}^{{b_1}} \times {p_2}^{{b_2}} \times \ldots \times {p_k}^{{b_k}}$

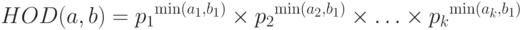
$HOD(a,b) = {p_1}^{\min ({a_1},{b_1})} \times {p_2}^{\min ({a_2},{b_1})} \times \ldots \times {p_k}^{\min ({a_k},{b_1})}$

Наименьшее общее кратное

Наименьшее общее кратное, НОК (a, b), — наименьшее целое число, кратное числам a и b. Используя разложение, мы также находим НОК (a, b).

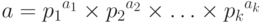
$a = {p_1}^{{a_1}} \times {p_2}^{{a_2}} \times \ldots \times {p_k}^{{a_k}}$

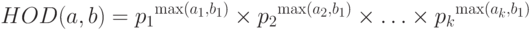
$HOD(a,b) = {p_1}^{\max ({a_1},{b_1})} \times {p_2}^{\max ({a_2},{b_1})} \times \ldots \times {p_k}^{\max ({a_k},{b_1})}$

Может быть доказано, что НОД (a,b) и НОК (a,b) связаны с друг другом, как это показано ниже:

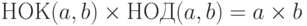
$НОК (a,b) \times НОД (a,b) = a \times b$

Методы разложения на множители

Поиск эффективных алгоритмов для разложения на множители больших составных чисел ведется давно. К сожалению, совершенный алгоритм для этого пока не найден. Хотя есть несколько алгоритмов, которые могут разложить число на множители, ни один не способен провести разложение достаточно больших чисел в разумное время. Позже мы увидим, что это хорошо для криптографии, потому что современные криптографические системы полагаются на этот факт. В этой секции мы даем несколько простых алгоритмов, которые проводят разложение составного числа. Цель состоит в том, чтобы сделать процесс разложения на множители менее трудоёмким.

Метод проверки делением

Самый простой и наименее эффективный алгоритм — метод разложения на множители проверкой делением. Мы просто пробуем все положительные целые числа начиная с 2, для того чтобы найти одно, которое делит n. После обсуждения решета Эратосфена мы знаем, что если n составное, то делитель будет простым числом $p \leqslant \sqrt n$ . Алгоритм 12.3 показывает этот метод. Алгоритм имеет два цикла: один внешний и один внутренний, находит уникальные множители в разложении; внутренняя петля находит повторяющиеся множители разложения. 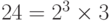Например, $24 = {2^3} \times 3$ . Внешний цикл множители 2 и 3. Внутренний цикл находит, что число 2 множитель.

12.3. Псевдокод для разложения на множители для метода проверки делением

Сложность. Метод проверки делением обычно хорош, если n < 2¹⁰, но он неэффективен и неосуществим для разложения больших целых чисел. Сложность алгоритма (приложение L) показательна.

Пример 12.29

Используйте алгоритм проверки делением, чтобы найти сомножители числа 1233.

Решение

Мы выполняем программу, основанную на алгоритме, и получаем следующий результат:

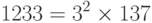
$1233 = {3^2} \times 137$

Пример 12.30

Используйте алгоритм проверки делением, чтобы найти сомножители 1523357784.

Решение

Мы выполняем программу, основанную на алгоритме, и получаем следующий результат:

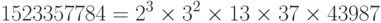
$1523357784 = {2^3} \times {3^2} \times 13 \times 37 \times 43987$

Метод Ферма

Метод Ферма разложения на множители (алгоритм 12.4) делит номер n на два положительных целых числа (a и b — не обязательно простые числа) так, чтобы 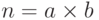$n = a \times b$ .

12.4. Алгоритм 12.4. Псевдокод для разложения на множители по методу Ферма

Метод Ферма основан на факте, что если мы можем найти x и y, такие, что n = x² – y², тогда мы имеем

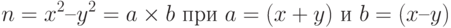
$n = x^{2} – y^{2}= a \times b\text{ при }a = (x + y)\text{ и }b = (x – y)$

Метод сводится к попытке найти два целых числа a и b, близкие друг к другу (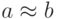 $a \approx b$ ). Начинаем с наименьшего целого числа, большего, чем $x = \sqrt n$ . Потом пробуем найти другое целое число y, такое, чтобы выполнялось уравнение y² = x² – n. В каждой итерации мы должны рассмотреть, является ли результат x² – n полным квадратом. Если мы находим такое значение для y, мы вычисляем a и b и выходим из цикла. Если мы не делаем этого, мы проводим другую итерацию.

Заметим, что метод не обязательно находит разложение на простые числа (каноническое разложение); алгоритм должен быть повторен рекурсивно для каждого из значений a и b, пока не будут найдены сомножители в виде простых чисел.

Сложность. Сложность метода Ферма является близкой к показательному закону (см. приложение L).

p – 1 Метод Полларда

В 1974 г. Джон Поллард разработал метод, который находит разложение числа p на простые числа. Метод основан на условии, что p – 1 не имеет сомножителя, большего, чем заранее определенное значение B, называемое границей. Алгоритм Полларда показывает, что в этом случае

p = НОД (2^B! – 1, n )

Алгоритм 12.5 показывает псевдокод для p – 1 метода Полларда разложения на множители. Когда мы выходим из второго цикла, в a сохраняется 2^B!.

12.5. Псевдокод для p – 1 метода Полларда разложения на множители

Сложность. Заметим, что этот метод требует сделать B – 1 операций возведения в степень (a = a^e mod n). Как мы увидим позже в этой лекции, есть быстрый алгоритм возведения в степень, который выполняет это за 2 1og₂ B операций. Метод также использует вычисления НОД, который требует n³ операций. Мы можем сказать, что сложность — так или иначе больше, чем O(B) или O(2ⁿ), где n_b — число битов в B. Другая проблема – этот алгоритм может заканчиваться сигналом об ошибке. Вероятность успеха очень мала, если B имеет значение, не очень близкое к величине 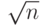$\sqrt n$ .

Пример 12.31

Используя p – 1 метод Полларда, найдите сомножители числа 57247159 с границей B = 8.

Решение

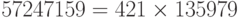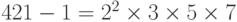Мы выполняем программу, основанную на рассмотренном выше алгоритме, и находим, что p = 421. Фактически $57247159 = 421 \times 135979$ . Обратите внимание, что 421 — простое число и p –1 не имеет ни одного сомножителя, большего 8, т.е. ( $421-1 = {2^2} \times 3 \times 5 \times 7$ ).

Дальше >>

Информационная безопасность

Математика криптографии и теория шифрования