|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Система с потерями и В-формула Эрланга
Введение
В-формула Эрланга основана на модели, которая содержит три элемента: структура, стратегия и нагрузка (рис.1.1).
- Структура. Мы рассматриваем систему из п идентичных обслуживающих приборов (серверы, каналы, слоты), работающих параллельно. Это называется гомогенной группой.
-
Стратегия. Вызов, достигая системы, принимается для обслуживания, если, по крайней мере, один канал свободен. Каждый вызов использует один и только один канал. Мы говорим, что группа имеет полную доступность. Часто используется термин полная готовность, но эта терминология будет использоваться только для случаев определения надежности соединения. Если все каналы заняты, система переполняется, и попытка вызова блокируется. Это блокированный вызов (отклоненный, потерянный) называется попыткой и исчезает из системы без всяких последствий. Последствия могли быть, если бы была принята стратегия с альтернативными маршрутами. Это стратегия - самая важная и применялась успешно много лет.
Она называется системой с потерями Эрланга или с явными потерями вызовов (LCC Lost Calls Cleared).
-
Нагрузка. Мы принимаем, что времена обслуживания являются экспоненциально распределенными с интенсивностью
 (соответствующим математическим ожиданием
(соответствующим математическим ожиданием  )- Процесс поступления вызовов - Пуассоновский процесс со скоростью
)- Процесс поступления вызовов - Пуассоновский процесс со скоростью 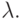 Этот тип нагрузки называется чистая Случайная Нагрузка Один (PCT-I - Риге Chance Traffic type One). Процесс нагрузки тогда становится простым Марковским процессом " гибели и размножения ", который имеет простое математическое описание.
Этот тип нагрузки называется чистая Случайная Нагрузка Один (PCT-I - Риге Chance Traffic type One). Процесс нагрузки тогда становится простым Марковским процессом " гибели и размножения ", который имеет простое математическое описание.
Определение предложенной нагрузки. Мы определяем предложенную нагрузку как нагрузку, которая поступает при бесконечном числе каналов (емкости) (2.2). В Эрланговской системе с потерями и Пуассоновским потоком вызовов это определение предложенной нагрузки, эквивалентно тому, что математическое ожидание поступления вызова за время пребывания в системе равно:
 |
( 7.1) |
Мы рассматриваем два случая:
Мы увидим позже, что эта модель нечувствительна к распределению времени пребывания в системе, то есть для вероятностей состояния важно только среднее время пребывания в системе. Тип распределения не имеет никакого значения для вероятностей состояния.
Критерии качества работы. Самые важные показатели уровня обслуживания для систем с потерями - потери по времени  , потери по вызовам
, потери по вызовам  и потери по нагрузке
и потери по нагрузке  . Все они равны между собой для системы с потерями Эрланга, поскольку в ней процесс поступления вызовов является наблюдаемым за среднее время Пуассоновским потоком (свойство PASTA - Poisson Arrival See Time Average, секция 6.3). Наиболее важные из этих свойств:
. Все они равны между собой для системы с потерями Эрланга, поскольку в ней процесс поступления вызовов является наблюдаемым за среднее время Пуассоновским потоком (свойство PASTA - Poisson Arrival See Time Average, секция 6.3). Наиболее важные из этих свойств:
- Пуассоновское поступление заявок происходит в случайные моменты времени;
- поступление нескольких заявок однородно распределено по интервалу;
- число заявок, которые уже находятся в системе, не влияет на процесс поступления вызовов.
Пуассоновское распределение
Мы предполагаем, что процесс поступления вызовов - Пуассоновский процесс, и что времена пребывания в системе имеет экспоненциальное распределение, то есть мы рассматриваем нагрузку PCT-I. Предполагается, что число каналов бесконечно, так что блокировка (перегрузка) отсутствует.
Диаграмма перехода состояния
Мы определяем состояние системы ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) как число занятых каналов
как число занятых каналов 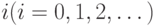 .
.
На рис.7.1 все состояния системы даны в виде окружностей и дуг от одного состояния до другого состояния, на которых показано значение интенсивности. Этот процесс простой (секция 5.1). Мы рассматриваем только переходы в соседние состояния.
Диаграмма переходов состояний схематически изображает переходы для системы с бесконечным числом каналов, Пуассоновским потоком вызовов (  ) и экспоненциально распределенными временами пребывания в системе (
) и экспоненциально распределенными временами пребывания в системе (  ).
).
Если мы предполагаем, что система находится в статистическом равновесии, то система будет находиться в состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) в течение определенного времени, пропорционального
в течение определенного времени, пропорционального 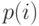 , где
, где 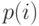 - вероятность существования системы в состоянии
- вероятность существования системы в состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) в случайный момент времени. Когда процесс находится в состоянии
в случайный момент времени. Когда процесс находится в состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) , он может перейти в следующий момент времени в состояние
, он может перейти в следующий момент времени в состояние ![[i+1] \lambda](/sites/default/files/tex_cache/44546207f1725a26b8c880471a07e2ef.png) раз в единицу времени или в состояние
раз в единицу времени или в состояние ![[i-1] i \mu](/sites/default/files/tex_cache/889f93dd8a05c7af47c1a24f7ff3d7d1.png) раз в единицу времени. В момент перехода из состояния в состояние процесс покидает состояние
раз в единицу времени. В момент перехода из состояния в состояние процесс покидает состояние ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) . Будущее развитие диаграммы состояний зависит только от существующего состояния, а не от того, как процесс прибыл в это состояние (Марковское свойство).
. Будущее развитие диаграммы состояний зависит только от существующего состояния, а не от того, как процесс прибыл в это состояние (Марковское свойство).
Уравнения, описывающие состояние системы, согласно предположению о статистическом равновесии могут быть получены двумя способами, которые основаны на принципе глобального равновесия.
а. Уравнения узла
В статистическом равновесии число переходов в состояние ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) в единицу времени равно числу переходов из состояния
в единицу времени равно числу переходов из состояния ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) . Вероятность состояния равновесия
. Вероятность состояния равновесия 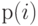 обозначает соотношение времени (отношение всего времени процесса к отношению в единицу времени), когда процесс находится в состоянии
обозначает соотношение времени (отношение всего времени процесса к отношению в единицу времени), когда процесс находится в состоянии ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) . Среднее число переходов из состояния [0] в состояние [1] равно
. Среднее число переходов из состояния [0] в состояние [1] равно 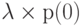 , в единицу времени, и среднее число переходов из состояния [1] в состояние
, в единицу времени, и среднее число переходов из состояния [1] в состояние ![[0] - \mu \times p(1)](/sites/default/files/tex_cache/2ec210b6ff7f067a2e9b7c2252109664.png) в единицу времени. Для состояния
в единицу времени. Для состояния ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) мы получаем следующее равновесие или уравнение равновесия:
мы получаем следующее равновесие или уравнение равновесия:
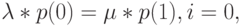 |
( 7.2) |
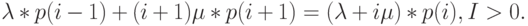 |
( 7.3) |
Уравнения узла также всегда применимы, для диаграмм перехода, где от одного состояния можно перейти в одно из нескольких состояний (несколько измерений), которые мы рассмотрим в более поздних лекциях.
б. Уравнения сечения
Во многих случаях мы можем применять простую структуру диаграммы перехода состояния. Применим фиктивное сечение, например, между состоянием ![[i-1]](/sites/default/files/tex_cache/7382a273ce9521676070f42215bf6956.png) и
и ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) (т.е. выделяем переходы от состояния
(т.е. выделяем переходы от состояния ![[0],[1], \dots , [i-1]](/sites/default/files/tex_cache/e9f209aa28086e860e361101da001e7b.png) ). Затем рассматриваем статистическое равновесие нагрузки от состояния
). Затем рассматриваем статистическое равновесие нагрузки от состояния ![[i - 1]](/sites/default/files/tex_cache/5fa2bc0b556e1a3c7defbcdee3564b2a.png) к
к ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) и изменение от состояния
и изменение от состояния ![[i]](/sites/default/files/tex_cache/47bb84b168a0b8f079f395dea29789b6.png) к
к ![[i-1]](/sites/default/files/tex_cache/7382a273ce9521676070f42215bf6956.png) . В статистическом равновесии мы, таким образом, имеем в единицу времени:
. В статистическом равновесии мы, таким образом, имеем в единицу времени:
 |
( 7.4) |
Уравнения сечения, прежде всего, используются для одномерных диаграмм перехода состояния, тогда как уравнения узла применимы к любой диаграмме.
Так как система всегда будет в некотором состоянии, мы имеем нормализующее ограничение:
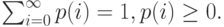 |
( 7.5) |
Можно заметить, что уравнения узла (7.3) включают три вероятности состояния, тогда как уравнения сечения (7.4) включают только две. Поэтому уравнения сечения решаются проще. Система с потерями всегда может перейти в состояние статистического равновесия, если процесс поступления вызовов независим от состояния системы. Математические условия для статистического равновесия в этой лекции не рассматриваются.
Вывод уравнений вероятностей состояния
Для одномерной диаграммы перехода состояний в большинстве случаев применяют подход на основе метода сечений. Из рис.7.1 мы получаем следующие уравнения равновесия:
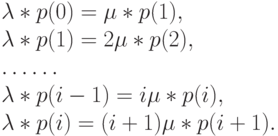
Используя выражение  и обозначая
и обозначая 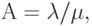 получаем
получаем
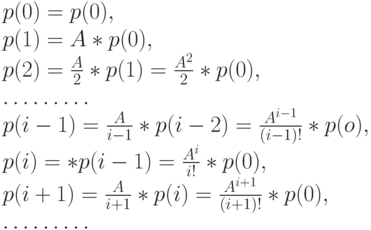
Из ограничения нормализации получаем 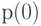 :
:
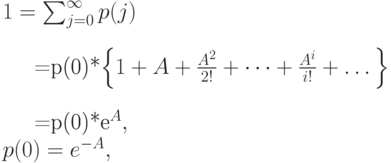
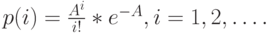 |
( 7.6) |
Число занятых каналов в случайный момент времени подчиняется Пуассоновскому распределению со средней величиной (6.17) и с дисперсией (6.18), равной  . Мы ранее показали, что число вызовов в фиксированном временном интервале также подчиняется Пуассоновскому распределению (6.16). Таким образом, Пуассоновское распределение справедливо и для времени, и для пространства. Мы, конечно, получили бы то же самое решение, используя уравнения узла.
. Мы ранее показали, что число вызовов в фиксированном временном интервале также подчиняется Пуассоновскому распределению (6.16). Таким образом, Пуассоновское распределение справедливо и для времени, и для пространства. Мы, конечно, получили бы то же самое решение, используя уравнения узла.


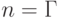 :
:  :Усеченное
:Усеченное 