Элементы теории реляционных баз данных: функциональные зависимости и декомпозиция без потерь

Замыкание множества функциональных зависимостей. Аксиомы Армстронга. Замыкание множества атрибутов

Замыканием множества FD S является множество FD S⁺, включающее все FD, логически выводимые из FD множества S .

Для начала приведем два примера FD, из которых следуют (или выводятся ) другие FD. Будем снова пользоваться отношением СЛУЖАЩИЕ_ПРОЕКТЫ. Для этого отношения выполняется, например, FD СЛУ_НОМ->{СЛУ_ЗАРП, ПРО_НОМ}. Из этой FD выводятся FD СЛУ_НОМ->СЛУ_ЗАРП и СЛУ_НОМ->ПРО_НОМ.

В отношении СЛУЖАЩИЕ_ПРОЕКТЫ имеется также пара FD СЛУ_НОМ->ПРО_НОМ и ПРО_НОМ->ПРОЕКТ_РУК. Из них выводится FD СЛУ_НОМ->ПРОЕКТ_РУК. Заметим, что FD вида СЛУ_НОМ->ПРОЕКТ_РУК называются транзитивными, поскольку ПРОЕКТ_РУК зависит от СЛУ_НОМ "транзитивно", через ПРО_НОМ.

FD A->C называется транзитивной, если существует такой атрибут B, что имеются функциональные зависимости A->B и B->C и отсутствует функциональная зависимость C->A .

Подход к решению проблемы поиска замыкания S⁺ множества FD S впервые предложил Вильям Армстронг^{1К сожалению, классическая статья Армстронга – W.W. Armstrong. "Dependency Structures of Data Base Relationships", Proc. IFIP Congress, Stockholm, Sweden, 1974 – так и не переведена на русский язык (на самом деле, ее нелегко найти и в оригинале). Поэтому я не могу рекомендовать ее для дополнительного чтения, хотя обязан сослаться.} . Им был предложен набор правил вывода новых FD из существующих (эти правила обычно называют аксиомами Армстронга, хотя справедливость правил доказывается на основе определения FD ). Обычно принято формулировать эти правила вывода в следующей форме. Пусть A, B и C являются (в общем случае, составными) атрибутами отношения r. Множества A, B и C могут иметь непустое пересечение. Для краткости будем обозначать через AB A UNION B. Тогда:

1. если 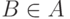, то A->B (рефлексивность);
2. если A->B, то AC->BC (дополнение);
3. если A->B и B->C, то A->C (транзитивность).

Истинность первой аксиомы Армстронга следует из того, что при 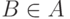FD A->B является тривиальной.

Справедливость второй аксиомы докажем от противного. Предположим, что FD AC->BC не соблюдается. Это означает, что в некотором допустимом теле отношения найдутся два кортежа t1 и t2, такие, что t1 {AC} = t2 {AC} (a), но 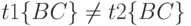(b) (здесь t {A} обозначает проекцию кортежа t на множество атрибутов A ). По аксиоме рефлексивности из равенства (a) следует, что t1 {A} = t2 {A}. Поскольку имеется FD A->B, должно соблюдаться равенство t1 {B} = t2 {B}. Тогда из неравенства (b) следует, что 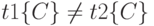, что противоречит наличию тривиальной FD AC->C. Следовательно, предположение об отсутствии FD AC->BC не является верным, и справедливость второй аксиомы доказана.

Аналогично докажем истинность третьей аксиомы Армстронга. Предположим, что FD A->C не соблюдается. Это означает, что в некотором допустимом теле отношения найдутся два кортежа t1 и t2, такие, что t1 {A} = t2 {A}, но 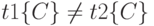. Но из наличия FD A->B следует, что t1 {B} = t2 {B}, а потому из наличия FD B->C следует, что t1 {C} = t2 {C}. Следовательно, предположение об отсутствии FD A->C не является верным, и справедливость третьей аксиомы доказана.

Можно доказать, что система правил вывода Армстронга полна и совершенна (sound and complete) в том смысле, что для данного множества FD S любая FD, потенциально выводимая из S, может быть выведена на основе аксиом Армстронга, и применение этих аксиом не может привести к выводу лишней FD. Тем не менее Дейт по практическим соображениям предложил расширить базовый набор правил вывода еще пятью правилами:

4. A->A (самодетерминированность) – прямо следует из правила (1);
5. если A->BC, то A->B и A->C (декомпозиция) – из правила (1) следует, что BC->B ; по правилу (3) A->B ; аналогично, из BC->С и правила (3) следует A->C ;
6. если A->B и A->C, то A->BC (объединение) – из правила (2) следует, что A->AB и AB->BC ; из правила (3) следует, что A->BC ;
7. если A->B и C->D, то AC->BD (композиция) – из правила (2) следует, что AС->BС и BC->BD ; из правила (3) следует, что AC->BD ;
8. если A->BC и B->D, то A->BCD (накопление) – из правила (2) следует, что BС->BCD ; из правила (3) следует, что A->BCD.

Пусть заданы отношение r, множество Z атрибутов этого отношения (подмножество заголовка r, или составной атрибут r ) и некоторое множество FD S, выполняемых для r. Тогда замыканием Z над S называется наибольшее множество Z⁺ таких атрибутов Y отношения r, что FD Z->Y входит в S⁺ .

Алгоритм вычисления Z⁺ очень прост. Один из его вариантов показан на рис. 6.2.

Рис. 6.2. Алгоритм построения замыкания атрибутов над заданным множеством FD

Докажем корректность алгоритма по индукции. На нулевом шаге Z[0] = Z, FD Z->Z[I], очевидно, принадлежит S⁺ ( тривиальная FD "выводится" из любого множества FD ). Пусть для некоторого K выполняется FD Z->Z[K], и пусть мы нашли в S такую FD A->B, что . Тогда можно представить Z[K] в виде AC, и, следовательно, выполняется FD Z->AC. Но по правилу (8) мы имеем FD Z->ACB, т.е. FD Z->(Z[K] UNION B) входит во множество S⁺, что переводит нас на следующий шаг индукции.

Пусть для примера имеется отношение с заголовком {A, B, C, D, E, F} и заданным множеством FD S = {A->D, AB->E, BF->E, CD->F, E->C}. Пусть требуется найти {AE}⁺ над S. На первом проходе тела цикла DO Z[1] равно AE. В теле цикла FOR EACH будут найдены FD A->D и E->C, и в конце цикла Z[1] станет равным ACDE. На втором проходе тела цикла DO при Z[2], равном ACDE, в теле цикла FOR EACH будет найдена FD CD->F, и в конце цикла Z[2] станет равным ACDEF. Следующий проход тела цикла DO не изменит Z[3], и Z⁺ ( {AE}⁺ ) будет равно ACDEF.

Алгоритм построения замыкания множества атрибутов Z над заданным множеством FD S помогает легко установить, входит ли заданная FD Z->B в замыкание S⁺. Очевидно, что необходимым и достаточным условием для этого является 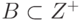, т. е. вхождение составного атрибута B в замыкание Z^{2Мы используем здесь знаки операций проверки включения множеств, что не совсем корректно, поскольку если, например, множество B состоит из одного элемента, то для его обозначения используется имя соответствующего атрибута, и в этом случае правильнее было бы использовать знак " 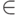" (проверка вхождения элемента во множество).} .

Суперключом отношения r называется любое подмножество K заголовка r, включающее, по меньшей мере, хотя бы один возможный ключ r .

Одно из следствий этого определения состоит в том, что подмножество K заголовка отношения r является суперключом тогда и только тогда, когда для любого атрибута A (возможно, составного) заголовка отношения r выполняется FD K->A. В терминах замыкания множества атрибутов K является суперключом тогда и только тогда, когда K⁺ совпадает с заголовком r.