Основные положения теории чисел, используемые в криптографии с открытым ключом

Цель лекции: напомнить читателю основные положения теории чисел, используемые в криптографии с открытым ключом

Простые и составные числа

Каждое натуральное число, большее единицы, делится по крайней мере на два числа: на 1 и на само себя. Если число не имеет делителей, кроме самого себя и единицы, то оно называется простым, а если у числа есть еще делители, то составным. Единица же не считается ни простым числом, ни составным. Например, числа 7, 29 — простые; числа 9, 15 — составные ( 9 делится на 3, 15 делится на 3 и на 5 ).

Интересный факт: если два простых числа отличаются на 2, то их называют числами-"близнецами". Чисел-"близнецов" не очень много. Например, "близнецами" являются 5 и 7, 29 и 31, 149 и 151, а также 242 206 083*2^{38 880}±1 (наибольшая найденная на момент написания учебного пособия пара "близнецов").

Не о всяком числе можно сразу сказать, простое оно или составное. Если число меньше ста, то, скорее всего мы сразу сможем ответить на этот вопрос. Однако с большими числами дело сложнее. Возьмем, например, число 2009. Простое оно или составное? Попробуем найти возможные делители этого числа среди первых простых чисел. 2009 определенно не делится на 2 (так как оно нечетное), на 3 (так как сумма его цифр 2+9=11 не делится на 3 ), на 5. А вот, попробовав разделить 2009 на 7, мы увидим, что в результате получается целый результат – 287. Таким образом, получен ответ: число 2009 – составное. В данном случае ответ получен достаточно быстро. Бывает, что проверка на простоту производится гораздо дольше, а для работы с большими целыми числами требуются даже специальные компьютерные программы.

Поиск больших простых чисел имеет важное значение для математики и не только. Например, в криптографии большие простые числа используются в алгоритмах шифрования с открытым ключом. Для обеспечения надежности шифрования там используются простые числа длиной до 1024 бит.

Перемножить два числа сравнительно нетрудно, особенно если у нас есть калькулятор, а числа не слишком велики. Существует и обратная задача – задача факторизации – нахождение двух или более чисел, дающих при перемножении заданное число. Эта задача гораздо труднее, чем перемножение чисел, и любому, кто пытался ее решить, об этом известно. Например, если от нас требуется умножить 67 на 113, то результат, 7571, будет получен, наверно, меньше чем за минуту. Если же от нас требуется найти два числа, произведение которых равно 7571, то, скорее всего, это займет у нас гораздо больше времени.

Поиск сомножителей числа n может вестись, например, перебором всех простых чисел до как в рассмотренном выше примере с числом 2009. Однако, если множители – большие простые числа, то на их поиск уйдет достаточно много времени.

Таким образом, факторизация большого числа требует значительных затрат времени даже в том случае, когда известно, что оно является произведением двух больших простых чисел.

Сложность задачи факторизации используется в некоторых криптографических алгоритмах, например, в системе шифрования RSA.

Основная теорема арифметики

Любое составное число можно составить из некоторого количества простых с помощью умножения. Например, составное число 2009 можно получить так:

2009 = 7 * 7 * 41

В математике рассматривается так называемая основная теорема арифметики, которая утверждает, что любое натуральное число ( n>1 ) либо само является простым, либо может быть разложено на произведение простых делителей, причем единственным способом (если не обращать внимания на порядок следования сомножителей).

Воспользовавшись обозначением степени, разложение числа 2009 на простые множители можно записать так:

2009 = 72 * 41

Разложение на множители называется каноническим, если все множители являются простыми и записаны в порядке возрастания.

Например, запишем каноническое разложение числа 150 на множители:

150 = 2 * 3 * 52

Взаимно простые числа и функция Эйлера

Два числа называются взаимно простыми, если они не имеют ни одного общего делителя кроме единицы.

Например, числа 11 и 12 взаимно просты (у них нет общих делителей кроме единицы), числа 30 и 35 — нет (у них есть общий делитель 5 ).

Исследованием закономерностей, связанных с целыми числами, долго занимался швейцарский математик Леонард Эйлер (Leonard Euler). Одним из вопросов, которым он интересовался, был следующий: сколько существует натуральных чисел, не превосходящих n и взаимно простых с n? Ответ на этот вопрос был получен Эйлером в 1763 году и этот ответ связан с каноническим разложением числа n на простые множители. Так, если

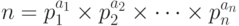
где p₁, p₂, ..., p_n – разные простые множители, то число натуральных чисел, не превосходящих n и взаимно простых с n можно точно определить по формуле

Число натуральных чисел, не превосходящих n и, взаимно простых с n, называется функцией Эйлера и обозначается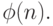

Например, найдем количество натуральных чисел, не превосходящих 12 и взаимно простых с 12. Из ряда натуральных чисел

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11

взаимно простыми (не имеющими общих делителей) с 12 будут только числа 1, 5, 7, 11. Их количество равно четырем. Таким образом

Теперь попробуем подсчитать

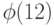
12 = 22 * 3.

Теперь подсчитаем функцию Эйлера :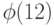

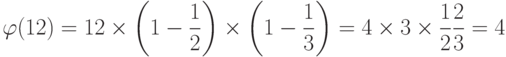
Значения, вычисленные путем простого перебора взаимно простых чисел и по формуле Эйлера, совпали. Это неудивительно, так как формула для вычисления функции Эйлера может быть доказана строго математически.

Формулу Эйлера удобно использовать для больших n, если известно разложение числа n на простые множители. Для криптографии формула Эйлера важна тем, что она позволяет легко получить число

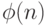
Следствие 1. Если p – простое число, то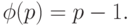

Действительно, если p – простое число, то его каноническое разложение состоит только из него самого. Тогда

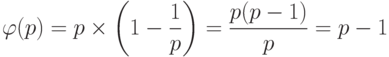
Следствие 2. Пусть р и q — два различных простых ( ). Тогда

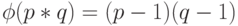
Эта формула объясняется следующим образом. Пусть р * q = N, где р и q — два различных простых ( ). Тогда

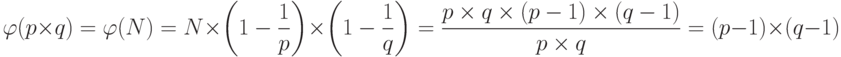
Рассмотрим несколько примеров использования следствий формулы Эйлера.

Пример 1. Найдем 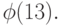13 – простое число, значит, используя следствие 1 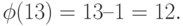Мы можем проверить себя (и Эйлера), выписав все числа, меньшие 13:

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12

и подсчитав все взаимно простые с ним. Их действительно 12.

Пример 2. Найдем 35 – составное число, значит, первое следствие нам не подходит. Однако 35 является произведением двух простых чисел: 35 = 5 * 7. Используя следствие 2, вычисляем :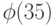

Проверяем, выписывая все числа, меньшие 35 и не имеющие с ним общих делителей:

1, 2, 3, 4, 6, 8, 9, 11, 12, 13, 16, 17, 18, 19, 22, 23, 24, 26, 27, 29, 31, 32, 33, 34.

Их действительно оказалось 24. На последнем примере видно, что использовать формулу Эйлера гораздо удобнее, чем рассматривать все числа из довольно большого диапазона и проверять на взаимную простоту.