Точка безубыточности и запас прочности. Имитационная модель риска
Рассчитаем запас прочности:
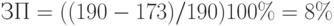
Предприятие может снизить объем продаж максимум на 8%, при большем снижении оно понесет убытки.
Другим методом оценки риска является построение имитационной модели. Имитационная модель — это модель, позволяющая описывать события так, как они происходили бы в реальности. Метод основан на использовании понятий теории вероятностей. Теория вероятностей – это раздел математики, изучающий случайные события и позволяющий прогнозировать их, что помогает принимать решения в условиях неопределенности [ 15 ] .
Этот метод оценки риска оптимален в ситуации выбора наименее рискованного варианта инвестирования. Если имеется несколько альтернативных инвестиционных проектов, то по каждому проекту разрабатываются сценарии развития (оптимистический, пессимистический и консервативный). Для каждого сценария рассчитывается чистый дисконтированный доход (ЧДД). На основе рассчитанных значений ЧДД рассчитываются следующие показатели:
- Размах вариации доходности инвестиционного проекта.
- Математическое ожидание доходности инвестиционного проекта.
- Дисперсия ожидаемой доходности.
- Среднеквадратическое отклонение.
- Коэффициент вариации.
Размах вариации – это разница между максимальным и минимальным значением случайной величины. Размах вариации доходности инвестиционного проекта определяется как разница между значениями ЧДД при оптимистическом и пессимистическом сценариях:

При нахождении математического ожидания доходности инвестиционного проекта подсчитывается сумма произведений ЧДД по каждому сценарию и вероятностей наступления сценариев:
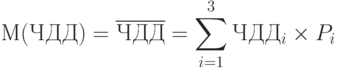
где i=1…3 – число сценариев;
Р – вероятность наступления сценария.
Среднеквадратическое отклонение рассчитывается как корень из дисперсии. Дисперсия характеризует разброс возможных значений случайной величины. Чтобы рассчитать среднеквадратическое отклонение доходности инвестиционного проекта, следует воспользоваться формулой:
![\sigma=\sqrt{\sum\limits^{3}_{i=1}\left [\left (ЧДД_i-\overline{ЧДД}\right)^2\times P_i\right]}](/sites/default/files/tex_cache/4a12d85f9c355a207a213bcb67fb00fb.png)
Коэффициент вариации представляет собой отношение среднеквадратического отклонения к математическом ожиданию:

Наиболее рискованным считается тот проект, у которого больше коэффициент вариации.
Пример. У инвестора имеется сумма 50 млн. руб. Он может инвестировать эту сумму либо в проект А, либо в проект В. Консервативный сценарий предполагает, что инвестор по проекту А получит ЧДД=10,5 млн. руб., а по проекту В – 9,8 млн. руб. При реализации пессимистического сценария ЧДД по проекту А составит -2,3 млн. руб., а по проекту В – ЧДД= -0,7 млн. руб. Реализация оптимистического сценария даст инвестору ЧДД=17,8 млн. руб. по проекту А и 13,6 млн. руб. по проекту В. Вероятность наступления консервативного сценария – 0,6, оптимистического – 0,3, пессимистического – 0,1. Выберите наименее рискованный вариант инвестирования.
Решение.
Рассчитаем размах вариации по проекту А:


Математическое ожидание ЧДД по проекту А:

Математическое ожидание ЧДД по проекту В:



Среднеквадратическое отклонение по проекту А:

Среднеквадратическое отклонение по проекту В:

Коэффициент вариации по проекту А:

Коэффициент вариации по проекту В:

Коэффициент вариации по проекту В меньше, чем по проекту А, значит, проект В является менее рискованным.
Краткие итоги:
- Точка безубыточности — это такой объем производства, при котором выручка равна себестоимости.
- Точку безубыточности можно определить аналитически и графически.
- Запас прочности показывает, на сколько процентов можно снизить объем продаж, прежде чем предприятие начнет нести убытки.
- Имитационная модель позволяет выбрать наименее рискованный вариант инвестирования.
Упражнения.
- Объем производства равен 300 шт. Общие затраты на производство и реализацию продукции – 10500 т.р., в том числе условно-постоянные затраты – 3500 т.р., условно-переменные затраты – 7000 т.р.. Цена единицы продукции – 20 т.р. за штуку. Определить точку безубыточности аналитически и графически, рассчитать запас прочности.
- У инвестора имеется сумма 80 млн. руб. Он может инвестировать эту сумму либо в проект А, либо в проект В. Консервативный сценарий предполагает, что инвестор по проекту А получит ЧДД=11,8 млн. руб., а по проекту В – 7,6 млн. руб. При реализации пессимистического сценария ЧДД по проекту А составит -5 млн. руб., а по проекту В – ЧДД= -2,3 млн. руб. Реализация оптимистического сценария даст инвестору ЧДД=20 млн. руб. по проекту А и 14 млн. руб. по проекту В. Вероятность наступления консервативного сценария – 0,6, оптимистического – 0,3, пессимистического – 0,1. Постройте имитационную модель. Рассчитайте размах вариации, математическое ожидание доходности, дисперсию, среднеквадратическое отклонение и коэффициент вариации. Выберите наименее рискованный вариант инвестирования.
Темы для курсовых работ, рефератов, эссе:
- Взаимосвязь объема продаж и показателей эффективности инвестиционного проекта.
- Имитационное моделирование различных областей риска.

