НОУ ИНТУИТ | Управление инвестиционным проектом. Лекция 13: Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 08.02.2012 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 87 студентам

| Поделиться |

Поддержать программу

Аннотация: Рассмотрена методика выбора наименее рискованного инвестиционного проекта на основе вероятностных критериев.

Ключевые слова: основной капитал, затраты, реальное значение, финансовые рынки, теория игр, значение, сценарий, максимум, прибыль, критерий Вальда, ПО, матрица, инвестиционный проект, разность, индекс доходности, доходность, величина риска, вероятность

Цель лекции: освоить методику расчета вероятностных критериев риска и выбора наименее рискованного варианта инвестирования.

Практика хозяйственной деятельности нередко вынуждает принимать решения, связанные с выбором оптимального варианта инвестирования в условиях риска и неопределенности. Инвестор, имеющий некоторую сумму, выбирает между несколькими инвестиционными проектами. Предприятие может стоять перед выбором направления инвестирования в основной, человеческий или природный капитал. Если направление инвестирования выбрано, возникают другие вопросы: так, если речь идет об инвестициях в основной капитал, то возникает проблема выбора конкретной техники и технологии. Инвестиции в человеческий капитал могут быть выражены либо в улучшении системы социального обеспечения работников предприятия, либо в их дополнительном образовании. Инвестиции в природный капитал могут быть направлены на строительство очистных сооружений или на приобретение нового оборудования, которое позволит снизить ресурсоемкость производства, и т.п. При этом неопределенность существует практически всегда. Параметры нового оборудования, уровень готовности персонала к работе на нем, затраты на монтаж можно прогнозировать, но зачастую реальные значения существенно отличаются от прогнозных. Оценка эффективности инвестиций в природный и человеческий капитал вообще является достаточно сложной экономической проблемой из-за трудности денежной оценки результата таких инвестиций. Кроме того, инвестор, как правило, не может прогнозировать макроэкономические изменения: структурные сдвиги, смену экономических циклов, процессы на международном валютно-финансовом рынке [ 13 ] . Таким образом, выбор оптимального варианта инвестирования — это нахождение проекта, удовлетворяющего инвестора с точки зрения доходности и риска.

Существенную помощь в решении подобных задач оказывают экономико-математические методы, а именно - использование теории игр и статистических решений. Методы теории игр позволяют глубже разобраться в ситуации, оценить каждое решение с разных точек зрения. В конечном итоге решающее значение имеет позиция инвестора относительно цели реализации проекта: либо он рассчитывает на оптимистический сценарий и хочет извлечь максимум выгоды (но в случае реализации негативных прогнозов он понесет существенные убытки), либо он хочет получить относительно небольшую, но гарантированную прибыль [ 14 ] .

В ситуации выбора оптимального варианта инвестирования целесообразно рассчитать несколько критериев: критерий Вальда, критерий Сэвиджа, критерий Гурвица, критерий Байеса, критерий Лапласа.

Предположим, имеется 4 варианта инвестирования — проекты А, Б, В, Г. По каждому проекту возможны 4 сценария развития ситуации — оптимистический, консервативный, пессимистический и смешанный. Для расчета вероятностных критериев риска нужно составить матрицу доходности и матрицу рисков. Элементами матрицы доходности являются индексы доходности (ИД). Строки матрицы доходности обозначают варианты инвестирования, а столбцы – сценарии развития ситуации ( таблица 13.1).

Таблица 13.1. Матрица доходности
	Оптимистич. сценарий	Консервативый сценарий	Пессимистич. сценарий	Смешанный сценарий
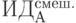Проект А	$ИД_А^{оптим.}$	$ИД_А^{консерв.}$	$ИД_А^{пессим.}$	$ИД_А^{смеш.}$
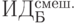Проект Б	$ИД_Б^{оптим.}$	$ИД_Б^{консерв.}$	$ИД_Б^{пессим.}$	$ИД_Б^{смеш.}$
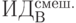Проект В	$ИД_В^{оптим.}$	$ИД_В^{консерв.}$	$ИД_В^{пессим.}$	$ИД_В^{смеш.}$
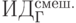Проект Г	$ИД_Г^{оптим.}$	$ИД_Г^{консерв.}$	$ИД_Г^{пессим.}$	$ИД_Г^{смеш.}$

Матрица рисков имеет такую же структуру, как и матрица доходности (в строках – инвестиционные проекты, в столбцах – сценарии). Элементом матрицы рисков является разность между максимально возможным индексом доходности по данному сценарию и индексом доходности данного проекта по этому же сценарию ( таблица 13.2).

Таблица 13.2. Матрица рисков
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	$ИД_{max}^{оптим.}-ИД_А^{оптим.}$	$ИД_{max}^{консерв.}-ИД_А^{консерв.}$	$ИД_{max}^{пессим.}-ИД_А^{пессим.}$	$ИД_{max}^{смеш.}-ИД_А^{смеш.}$
Проект Б	$ИД_{max}^{оптим.}-ИД_Б^{оптим.}$	$ИД_{max}^{консерв.}-ИД_Б^{консерв.}$	$ИД_{max}^{пессим.}-ИД_Б^{пессим.}$	$ИД_{max}^{смеш.}-ИД_Б^{смеш.}$
Проект В	$ИД_{max}^{оптим.}-ИД_В^{оптим.}$	$ИД_{max}^{консерв.}-ИД_В^{консерв.}$	$ИД_{max}^{пессим.}-ИД_В^{пессим.}$	$ИД_{max}^{смеш.}-ИД_В^{смеш.}$
Проект Г	$ИД_{max}^{оптим.}-ИД_Г^{оптим.}$	$ИД_{max}^{консерв.}-ИД_Г^{консерв.}$	$ИД_{max}^{пессим.}-ИД_Г^{пессим.}$	$ИД_{max}^{смеш.}-ИД_Г^{смеш.}$

Критерий Вальда олицетворяет позицию "крайнего пессимизма", позволяя определить, какой проект даст наибольший доход при реализации пессимистического сценария:

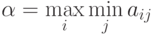
$\alpha=\max_{i}\min_{j}a_{ij}$

где $a_{ij}$ – элементы матрицы доходности.

Критерий Сэвиджа также является критерием "крайнего пессимизма", но этот критерий советует при выборе оптимального решения ориентироваться не на доходность, а на риск. Использование критерия Сэвиджа оправдано в том случае, если инвестор хочет в любом случае избежать большого риска и готов ради этого упустить некоторую выгоду. Оптимальным считается тот инвестиционный проект, для которого величина риска при реализации пессимистического сценария минимальна:

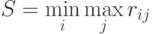
$S=\min_{i}\max_{j}r_{ij}$

где 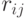$r_{ij}$ – элементы матрицы рисков.

Критерий Гурвица рекомендует не рассматривать ситуацию ни с позиции "крайнего пессимизма", ни "крайнего оптимизма", то есть советует не рассчитывать ни на наилучшее, ни на наихудшее развитие событий. При расчете критерия Гурвица используется так называемый "коэффициент пессимизма" 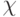$\chi$ , значения которого находятся в интервале между нулем и единицей:

$H=\max_{i}[\lambda\min_{j}a_{ij}+(1-\lambda)\max_{j}a_{ij}]$

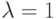При $\lambda=1$ критерий Гурвица превращается в критерий Вальда, то есть в критерий "крайнего пессимизма". При 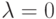$\lambda=0$ – в критерий "крайнего оптимизма", рекомендующий выбирать инвестиционный проект, дающий наибольший доход при реализации оптимистического сценария. Коэффициент пессимизма ? выбирается исходя из склонности инвестора к риску – чем меньше эта склонность, тем ближе к единице значение $\chi$ .

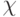Критерий Байеса рекомендует выбирать тот инвестиционный проект, для которого математическое ожидание индекса доходности максимально:

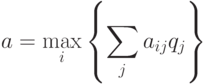
$a=\max_{i}\left\{\sum\limits_{j}a_{ij}q_j\right\}$

где $a_{ij}$ – элементы матрицы доходности;

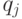
– вероятности наступления сценариев.

Критерий Лапласа отличается от критерия Байеса тем, что вероятности наступления сценариев принимаются равными.

Пример. Дана матрица доходности ( таблица 13.3). Составить матрицу рисков и рассчитать критерии Вальда, Сэвиджа, Гурвица, Байеса, Лапласа. Коэффициент пессимизма равен 0,6. Вероятность наступления оптимистического сценария – 0,2, пессимистического – 0,2, смешанного – 0,1, консервативного – 0,5.

Таблица 13.3. Матрица доходности
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	2,03	1,03	-0,3	1,01
Проект Б	2,04	1,04	-0,4	1,02
Проект В	2,05	1,05	-0,5	1,15
Проект Г	2,06	1,06	-0,6	1,32

Решение.

1. Определим максимальное значение по каждому столбцу матрицы доходности. Получим 2,06 для оптимистического сценария, 1,06 – для консервативного, -0,3 – для пессимистического и 1,32 для смешанного. Далее вычитаем из максимального по столбцу значения каждый элемент этого столбца. Например, определим риск по проекту А для оптимистического сценария:

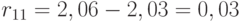
$r_{11}=2,06-2,03=0,03$

Аналогично определяем каждый элемент матрицы рисков и сводим полученные значения в таблицу 13.4 .

Таблица 13.4. Матрица рисков
	Оптимистич. сценарий	Консервативный сценарий	Пессимистич. сценарий	Смешанный сценарий
Проект А	0,03	0,03	0,00	0,31
Проект Б	0,02	0,02	0,10	0,30
Проект В	0,01	0,01	0,20	0,17
Проект Г	0,00	0,00	0,30	0,00

Дальше >>

Менеджмент для ИТ-директора

Управление инвестиционным проектом

Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Вопросы и ответы

Студенты

Авторизоваться

Менеджмент для ИТ-директора

Управление инвестиционным проектом

Принятие оптимального инвестиционного решения в условиях риска и неопределенности

Вопросы и ответы

Студенты