|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Методы повышения экономической эффективности ПКС на основе моделирования и оптимизации внутрикорпоративных потоков
Можно подумать, что величина партии должна быть равна имеющейся сумме денежных средств, однако это не так. Покажем, что максимум продаж после единовременной поставки (это участок 4) достигается, если величина партии больше имеющейся суммы денег.
После поставки партии в момент 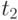 запас товаров скачкообразно увеличивается (см.
рис. 5.5). В результате интенсивность потока продаж возрастает в соответствии с (5.16). Интенсивность потока поставок после момента
запас товаров скачкообразно увеличивается (см.
рис. 5.5). В результате интенсивность потока продаж возрастает в соответствии с (5.16). Интенсивность потока поставок после момента  для сбалансированности запаса товаров необходимо поддерживать равной новой, увеличенной интенсивности потока продаж. Так как оплата поставок запаздывает относительно поставок, то в момент
для сбалансированности запаса товаров необходимо поддерживать равной новой, увеличенной интенсивности потока продаж. Так как оплата поставок запаздывает относительно поставок, то в момент  необходимо единовременно истратить сумму на оплату партии, после чего интенсивность потока оплаты становится равной новой повышенной интенсивности поставок. Эта сумма может быть не более величины денежных средств в момент оплаты
необходимо единовременно истратить сумму на оплату партии, после чего интенсивность потока оплаты становится равной новой повышенной интенсивности поставок. Эта сумма может быть не более величины денежных средств в момент оплаты  , исходя из чего определяется максимально возможная величина партии, и, следовательно, максимальный прирост продаж. Величина денежных средств к моменту
, исходя из чего определяется максимально возможная величина партии, и, следовательно, максимальный прирост продаж. Величина денежных средств к моменту  складывается из суммы, имевшейся на участке 3 и линейного прироста на отрезке
складывается из суммы, имевшейся на участке 3 и линейного прироста на отрезке ![[t_{2}, t_{2} + T_{K}]](/sites/default/files/tex_cache/1a8c46f8f39c15c0a7ac21df54f620a8.png) . Прирост возникает вследствие превышения притока денежных средств над оттоком: приток увеличился в результате поставки партии и прироста запаса товаров, а отток оставался на прежнем, пониженном уровне участка 3, поскольку в течение периода
. Прирост возникает вследствие превышения притока денежных средств над оттоком: приток увеличился в результате поставки партии и прироста запаса товаров, а отток оставался на прежнем, пониженном уровне участка 3, поскольку в течение периода 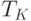 оплачивались "старые" поставки. Исходя из сказанного, величина партии, обозначаемая через
оплачивались "старые" поставки. Исходя из сказанного, величина партии, обозначаемая через  , находится следующим образом. Интенсивность потока продаж на участке 4, на основании (5.16):
, находится следующим образом. Интенсивность потока продаж на участке 4, на основании (5.16):
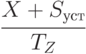 |
( 5.33) |
Скорость роста денежных средств, равная интенсивности продаж минус интенсивность оплаты:
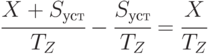 |
( 5.34) |
Прирост денежных средств на участке 4 за время 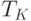 со скоростью (5.34):
со скоростью (5.34):
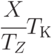 |
( 5.35) |
Сумма денежных средств к моменту оплаты партии  , равная денежным средствам на участке 3 плюс прирост:
, равная денежным средствам на участке 3 плюс прирост:
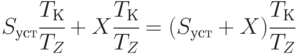 |
( 5.36) |
Эта сумма должна быть равна величине партии:
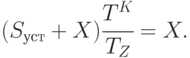 |
( 5.37) |
Откуда
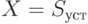 |
( 5.38) |
Так как 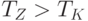 , то найденная таким образом величина больше денежных средств на участке 3, равных
, то найденная таким образом величина больше денежных средств на участке 3, равных 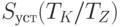 .
.
Интенсивность продаж получается подстановкой (5.38) в (5.33):
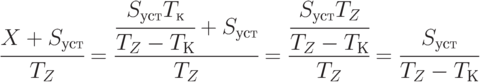 |
( 5.39) |
На участке 4 реализуется максимально возможная интенсивность продаж, поэтому можно рассчитать максимальный прирост продаж, получаемый за счет товарного кредита по сравнению со случаем, когда отсрочка оплаты поставок не предоставляется:
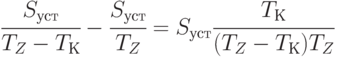 |
( 5.40) |
Это выражение позволяет выяснить, как изменяется прирост продаж при различных значениях периода отсрочки оплаты. Если значение 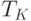 приближается к значению
приближается к значению 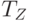 , то согласно (5.40) прирост продаж устремляется к бесконечности. Если значение
, то согласно (5.40) прирост продаж устремляется к бесконечности. Если значение 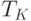 приближается к нулю, то к нулю устремляется и прирост.
приближается к нулю, то к нулю устремляется и прирост.
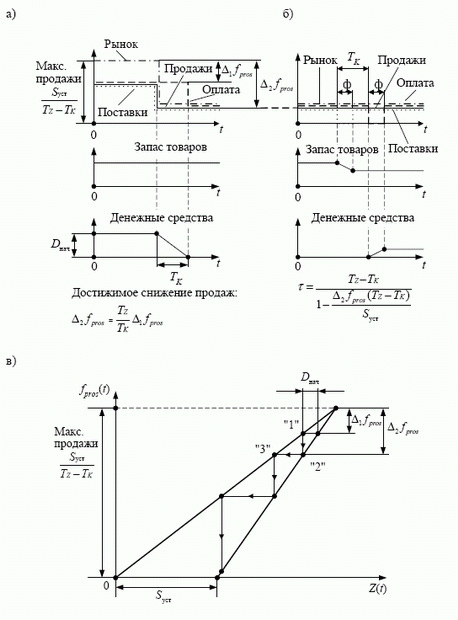
Получение максимальных продаж на участке 4 анализировалось путем исследования процессов, происходящих во времени в системе потоков предприятия. Условия обеспечения максимальных продаж можно получить более простым способом, на базе учета баланса активов и источников средств с помощью диаграммы ( рис. 5.5, в), которую можно считать развитием графического анализа ( рис. 5.5, б) на случай товарного кредита. Анализ основывается на совместном изображении графиков зависимостей источников средств и величины активов от интенсивностей потоков. Метод анализа, называемый методом поточнозапасных характеристик, более подробно обосновывается и разрабатывается в последующих разделах настоящей лекции.
В правой части участка 4 после момента  интенсивности потоков продаж, поставок и оплаты равны при нулевых денежных средствах, то есть с помощью собственных средств и кредиторской задолженности финансируется только запас товаров, и выражение (5.25), учитывая (5.16), записывается в виде:
интенсивности потоков продаж, поставок и оплаты равны при нулевых денежных средствах, то есть с помощью собственных средств и кредиторской задолженности финансируется только запас товаров, и выражение (5.25), учитывая (5.16), записывается в виде:
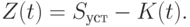 |
( 5.41) |
Из этого условия можно найти интенсивность потока и, следовательно, режим функционирования с максимальными продажами, принимая во внимание, вопервых, зависимость запаса от искомой интенсивности потока согласно (5.16) (случай равенства), и, вовторых, зависимость величины кредиторской задолженности от потока. Наличие последней зависимости очевидно и означает, что объем финансирования товарным кредитом связан с интенсивностью потоков, однако в явном математическом виде такая зависимость пока не рассматривалась. Выяснить эту зависимость можно, основываясь на представлении о времени обновления кредиторской задолженности, очевидно, равном периоду отсрочки оплаты 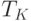 . Искомым потоком, обозначим его через
. Искомым потоком, обозначим его через  , кредиторская задолженность полностью обновляется за время
, кредиторская задолженность полностью обновляется за время 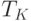
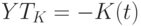 |
( 5.42) |
для любого момента участка 4, 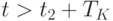 . Подставляя это в (5.41) и подставляя вместо
. Подставляя это в (5.41) и подставляя вместо  его выражение из (5.16), получаем, учитывая
его выражение из (5.16), получаем, учитывая 
 |
( 5.43) |
По этому соотношению сформирована диаграмма (
рис. 5.5, в). Левая прямая линия, проходящая через начало координат, показывает зависимость запаса, то есть потребности в финансировании, от величины потока, откладываемой по вертикальной оси; при этом величина запаса отмечается по горизонтальной оси, а сама прямая линия соответствует левой части (5.43). Очевидно, это та же самая прямая линия, что и на
рис. 5.5, б . Линия проводится под углом 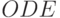 к вертикали, тангенс которого равен
к вертикали, тангенс которого равен
 |
( 5.44) |
Правая прямая линия соответствует правой части (5.43) и может интерпретироваться как суммарное финансирование, складывающееся из постоянной части  и переменной линейной составляющей финансирования товарным кредитом, прямо пропорциональной потоку. Линия проводится через точку
и переменной линейной составляющей финансирования товарным кредитом, прямо пропорциональной потоку. Линия проводится через точку 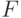 под углом
под углом 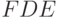 , тангенс которого равен
, тангенс которого равен
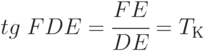 |
( 5.45) |
Правая линия имеет меньший наклон к вертикальной оси, так как 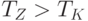 , и поэтому линии имеют точку пересечения
, и поэтому линии имеют точку пересечения  , соответствующую равенству (5.43). Эта точка определяет искомую максимальную интенсивность потока продаж, которая из геометрических соображений находится следующим образом. Из (5.44) и (5.45), соответственно
, соответствующую равенству (5.43). Эта точка определяет искомую максимальную интенсивность потока продаж, которая из геометрических соображений находится следующим образом. Из (5.44) и (5.45), соответственно
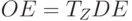
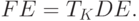 |
( 5.46) |
Вычитая из первого равенства второе,
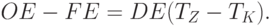
Так как  , а
, а 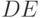 - искомая интенсивность продаж, то
- искомая интенсивность продаж, то
 |
( 5.47) |
что соответствует (5.39).
Величина партии на диаграмме изображается отрезком 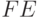 и находится подстановкой (5.47) в (5.46)
и находится подстановкой (5.47) в (5.46)

что совпадает с (5.38).
Аналогично тому, как точка 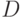 диаграммы изображает состояние предприятия на участке 4, с помощью точек
диаграммы изображает состояние предприятия на участке 4, с помощью точек 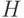 и
и 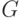 можно отобразить функционирование на участках 1 и 3 соответственно. Более того, диаграмма позволяет изобразить состояние предприятия не только при условии поддержания максимальных продаж, допустимых наличным запасом, как это считалось до сих пор, и что означает рассмотрение неравенства (5.16) в варианте строгого равенства. Неравенство (5.16) на диаграмме показано штриховкой выше линии
можно отобразить функционирование на участках 1 и 3 соответственно. Более того, диаграмма позволяет изобразить состояние предприятия не только при условии поддержания максимальных продаж, допустимых наличным запасом, как это считалось до сих пор, и что означает рассмотрение неравенства (5.16) в варианте строгого равенства. Неравенство (5.16) на диаграмме показано штриховкой выше линии 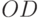 в знак того, что изображающие точки не могут находиться выше линии. Линия
в знак того, что изображающие точки не могут находиться выше линии. Линия 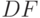 заштрихована справа, демонстрируя непревышение суммы активов имеющимися источниками средств. Следовательно, изображающая точка может находиться внутри треугольника
заштрихована справа, демонстрируя непревышение суммы активов имеющимися источниками средств. Следовательно, изображающая точка может находиться внутри треугольника 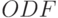 , расстояние от нее до правой линии показывает величину денежных средств, а проекция на горизонтальную ось дает величину запаса товаров.
, расстояние от нее до правой линии показывает величину денежных средств, а проекция на горизонтальную ось дает величину запаса товаров.
В момент 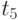 возникает ситуация, аналогичная таковой в случае резкого уменьшения спроса. Эта ситуация анализируется ниже путем сравнения притока и оттока денежных средств. Рынок уменьшается до величины, меньшей, чем интенсивность продаж на участке 4. Это означает, что из двух неравенств (5.16) и (5.17) актуальным становится последнее, то есть фактором, ограничивающим продажи, оказывается не величина запаса, а рынок.
возникает ситуация, аналогичная таковой в случае резкого уменьшения спроса. Эта ситуация анализируется ниже путем сравнения притока и оттока денежных средств. Рынок уменьшается до величины, меньшей, чем интенсивность продаж на участке 4. Это означает, что из двух неравенств (5.16) и (5.17) актуальным становится последнее, то есть фактором, ограничивающим продажи, оказывается не величина запаса, а рынок.
Непосредственно после момента уменьшения рынка, в малой окрестности справа от точки 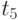 на оси времени, продажи становятся равными рынку
на оси времени, продажи становятся равными рынку 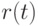 , и, следовательно, оказываются меньше, чем продажи и поставки на участке 4. В эти же моменты малой окрестности оплата поставок остается равной поставкам на участке 4, то есть меньше продаж, поскольку оплата отстает от поставок. Следовательно, отток денежных средств, в виде оплаты, становится больше притока по поставкам. Так как в момент
, и, следовательно, оказываются меньше, чем продажи и поставки на участке 4. В эти же моменты малой окрестности оплата поставок остается равной поставкам на участке 4, то есть меньше продаж, поскольку оплата отстает от поставок. Следовательно, отток денежных средств, в виде оплаты, становится больше притока по поставкам. Так как в момент 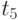 запас денег
запас денег  нулевой, то в результате возникает дефицит денежных средств. Это можно интерпретировать как ситуацию неплатежеспособности: поставки не могут быть оплачены в срок. Дефицит возникает независимо от того, на сколько сильно рынок уменьшился по сравнению с продажами на предшествующем участке 4, поскольку на участке 4 денежные средства в точности равны нулю. Если на участке 4 был бы некоторый запас денежных средств, то возникновение дефицита не являлось бы неизбежным. Однако максимум продаж на этом участке не достигается.
нулевой, то в результате возникает дефицит денежных средств. Это можно интерпретировать как ситуацию неплатежеспособности: поставки не могут быть оплачены в срок. Дефицит возникает независимо от того, на сколько сильно рынок уменьшился по сравнению с продажами на предшествующем участке 4, поскольку на участке 4 денежные средства в точности равны нулю. Если на участке 4 был бы некоторый запас денежных средств, то возникновение дефицита не являлось бы неизбежным. Однако максимум продаж на этом участке не достигается.
Теперь можно сделать вывод: максимум продаж на участке 4 достигнут ценой недопустимо высокого риска неплатежеспособности, учитывая, что влияние рынка в виде резких падений спроса наблюдается часто и повсеместно.
Функционирование предприятия в точке 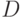 (
рис. 5.5, в) без некоторого запаса денежных средств недопустимо, что хорошо известно в научном финансовом менеджменте и объясняется возможностью непредвиденных ситуаций. Однако там отсутствует количественный анализ в рамках систем потоков предприятия.
(
рис. 5.5, в) без некоторого запаса денежных средств недопустимо, что хорошо известно в научном финансовом менеджменте и объясняется возможностью непредвиденных ситуаций. Однако там отсутствует количественный анализ в рамках систем потоков предприятия.
Как следствие выясненной недопустимости функционирования в точке  , возникают вопросы о величине необходимых запасов денежных средств на участке 4 и об управлении потоками предприятия при переходе к пониженному рынку. Очевидно, оба этих вопроса следует решать в связи с потерями от снижения продаж на участке 4.
, возникают вопросы о величине необходимых запасов денежных средств на участке 4 и об управлении потоками предприятия при переходе к пониженному рынку. Очевидно, оба этих вопроса следует решать в связи с потерями от снижения продаж на участке 4.
Пусть предприятие на участке 4 функционирует с некоторой интенсивностью продаж, меньшей максимальной; поэтому может существовать некоторый запас денежных средств. Применительно к диаграмме (см.
рис. 5.5, в) это означает, что изображающая точка находится ниже точки  . Выясним, на сколько могут быть снижены продажи в момент
. Выясним, на сколько могут быть снижены продажи в момент 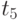 до некоторого нового постоянного уровня, если запас денежных средств максимальный для данных продаж, то есть изображающая точка находится в крайнем левом положении (
рис. 5.7, в, точка "1"). Обозначим через
до некоторого нового постоянного уровня, если запас денежных средств максимальный для данных продаж, то есть изображающая точка находится в крайнем левом положении (
рис. 5.7, в, точка "1"). Обозначим через 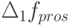 разность между максимальными продажами
разность между максимальными продажами 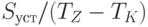 и интенсивностью потока продаж в точке "1", эту разность можно назвать "недобором максимальных продаж". Искомое снижение продаж по отношению к максимуму
и интенсивностью потока продаж в точке "1", эту разность можно назвать "недобором максимальных продаж". Искомое снижение продаж по отношению к максимуму 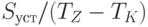 обозначим через
обозначим через 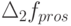 .
.
-
а ) - синхронное уменьшение продаж и поставок при
 ,
, -
б ) - конвертация запаса товаров в денежные средства при
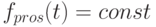 ,
, - в ) - последовательное применение управлений а ) и б )
После момента снижения продаж приток денежных средств уменьшается, а отток в виде оплаты поставок в течение времени 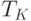 остается более высоким. За счет этого запас денежных средств равномерно уменьшается. Максимально возможное в условиях снижение продаж
остается более высоким. За счет этого запас денежных средств равномерно уменьшается. Максимально возможное в условиях снижение продаж 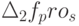 находится из условия уменьшения запаса денежных средств до нуля. Обозначим
находится из условия уменьшения запаса денежных средств до нуля. Обозначим 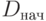 запас денежных средств при функционировании предприятия в точке "1", он находится исходя из подобия треугольников (см.
рис. 5.7, в):
запас денежных средств при функционировании предприятия в точке "1", он находится исходя из подобия треугольников (см.
рис. 5.7, в):
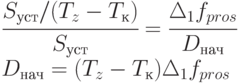 |
( 5.48) |
Скорость уменьшения денежных средств равна разности "новой" и "старой" интенсивности продаж:
![\left [ \cfrac{S_{уст}}{T_z - T_к} - \Delta_1 f_{pros} \right ] - \left [ \cfrac{S_{уст}}{T_z - T_к} - \Delta_2 f_{pros} \right ] =
\Delta_2 f_{pros} - \Delta_1 f_{pros}](/sites/default/files/tex_cache/a237296f4e881c7bdcec7be814e45680.png)
Уменьшаясь с этой скоростью, денежные средства в количестве (5.48) за время 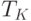 должны быть полностью израсходованы:
должны быть полностью израсходованы:
![\left [ \cfrac{S_{уст}}{T_Z - T_К} - \Delta_1 f_{pros} \right ] - \left [ \cfrac{S_{уст}}{T_Z - T_К} - \Delta_2 f_{pros} \right ] =
\Delta_2 f_{pros} - \Delta_1 f_{pros}](/sites/default/files/tex_cache/b49e236cea3adb3eb5342d7f0cfc9439.png)
где 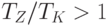 .
.
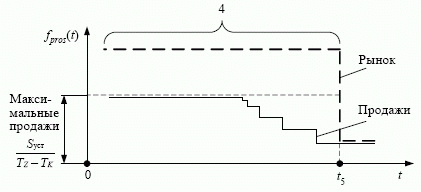
Чтобы после полного расходования денежных средств они оставались на нулевом уровне, оплата должна стать равной продажам. Это возможно, если в момент уменьшения продаж поставки уменьшить до такого же уровня. Это в свою очередь означает, что после момента 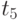 запас товаров остается неизменным. Графики изменения переменных величин в описанном переходе от большей интенсивности продаж к меньшей изображены на
рис. 5.7(а), а сам переход можно назвать синхронным ступенчатым уменьшением продаж и поставок. На диаграмме (
рис. 5.7, в) переход представляет собой движение изображающей точки по вертикальной линии из положения "1" в новое положение, обозначенное точкой "2", поскольку запас товаров оставался постоянным. В новом положении величина запасов товаров избыточна для данной интенсивности продаж, изображающая точка находится в крайнем правом положении на горизонтальной линии, что соответствует нулевому запасу денежных средств и недопустимо по упомянутым выше причинам. Однако весь избыточный запас товаров теперь может быть конвертирован в денежные средства (при неизменной интенсивности продаж) путем временного прекращения поставок, что на диаграмме (
рис. 5.7, в) показано как перемещение изображающей точки из положения "2" в положение "3", а соответствующие графики изменения переменных величин показаны на
рис. 5.7, б.
запас товаров остается неизменным. Графики изменения переменных величин в описанном переходе от большей интенсивности продаж к меньшей изображены на
рис. 5.7(а), а сам переход можно назвать синхронным ступенчатым уменьшением продаж и поставок. На диаграмме (
рис. 5.7, в) переход представляет собой движение изображающей точки по вертикальной линии из положения "1" в новое положение, обозначенное точкой "2", поскольку запас товаров оставался постоянным. В новом положении величина запасов товаров избыточна для данной интенсивности продаж, изображающая точка находится в крайнем правом положении на горизонтальной линии, что соответствует нулевому запасу денежных средств и недопустимо по упомянутым выше причинам. Однако весь избыточный запас товаров теперь может быть конвертирован в денежные средства (при неизменной интенсивности продаж) путем временного прекращения поставок, что на диаграмме (
рис. 5.7, в) показано как перемещение изображающей точки из положения "2" в положение "3", а соответствующие графики изменения переменных величин показаны на
рис. 5.7, б.
После момента прекращения поставок продажи остаются на постоянном уровне точки "2", в результате запас товаров линейно уменьшается. В течение отрезка времени 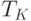 после этого момента оплата остается на постоянном уровне, соответствующем положению точки "2", то есть приток и отток денежных средств равны и денежные средства остаются нулевыми. Поставки должны оставаться нулевыми в течение некоторого отрезка времени, обозначаемого
после этого момента оплата остается на постоянном уровне, соответствующем положению точки "2", то есть приток и отток денежных средств равны и денежные средства остаются нулевыми. Поставки должны оставаться нулевыми в течение некоторого отрезка времени, обозначаемого 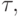 в течение которого весь избыточный запас товаров будет израсходован, и новый уровень запаса уменьшится до минимально необходимого для данных продаж. Исходя из этого условия находится величина
в течение которого весь избыточный запас товаров будет израсходован, и новый уровень запаса уменьшится до минимально необходимого для данных продаж. Исходя из этого условия находится величина 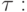
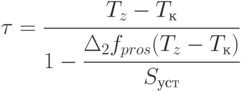 |
( 5.50) |
Таким образом, выполненный анализ (см.
рис. 5.7) позволяет установить, что резкое, "ступенчатое" уменьшение продаж в момент 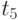 (см.
рис. 5.5, а) возможно на максимальную величину, определяемую соотношением (5.49), а в результате последовательного применения управлений потоками по
рис. 5.7, а и
рис. 5.7, б предприятие переходит из состояния "1" в состояние "3". Существенно, что новое состояние можно считать допустимым, и оно подобно исходному, так как имеется запас денежных средств, максимальный при данных потоках продаж.
(см.
рис. 5.5, а) возможно на максимальную величину, определяемую соотношением (5.49), а в результате последовательного применения управлений потоками по
рис. 5.7, а и
рис. 5.7, б предприятие переходит из состояния "1" в состояние "3". Существенно, что новое состояние можно считать допустимым, и оно подобно исходному, так как имеется запас денежных средств, максимальный при данных потоках продаж.
Оценить значение величины возможного снижения продаж можно, если выяснить значения коэффициента 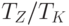 в выражении (5.49). Покажем, что эти возможные значения находятся из известного интервала практически реализуемых
значений аналитического коэффициента покрытия, рассчитываемого как отношение суммы оборотных активов к сумме текущих (краткосрочных) пассивов. Если изображающая точка находится в точке
в выражении (5.49). Покажем, что эти возможные значения находятся из известного интервала практически реализуемых
значений аналитического коэффициента покрытия, рассчитываемого как отношение суммы оборотных активов к сумме текущих (краткосрочных) пассивов. Если изображающая точка находится в точке 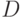 (см рис. 5.5, в), то
(см рис. 5.5, в), то
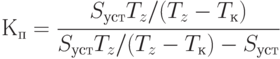 |
( 5.51) |
где  - коэффициент покрытия, в числителе выражения (5.51) записана сумма активов, а в знаменателе - пассив в виде суммы кредиторской задолженности.
- коэффициент покрытия, в числителе выражения (5.51) записана сумма активов, а в знаменателе - пассив в виде суммы кредиторской задолженности.
Выполнив элементарные преобразования правой части (5.51), получим:
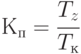 |
( 5.52) |
Известно, что коэффициент покрытия изменяется в пределах 1,5-2,0, и поэтому, согласно (5.52), в этих же пределах может находиться коэффициент
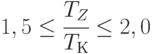 |
( 5.53) |
Оценка (5.53) сделана для случая функционирования предприятия в недопустимой точке  . Однако, учитывая, что доля денежных средств невелика и практически составляет единицы процентов от обязательств, и, следовательно, точка "1" находится вблизи вершины треугольника (точки
. Однако, учитывая, что доля денежных средств невелика и практически составляет единицы процентов от обязательств, и, следовательно, точка "1" находится вблизи вершины треугольника (точки 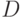 на
рис. 5.5, в), оценку (5.53) можно принять для предприятия в целом. Следовательно, снижение продаж в соответствии с выражением (5.49) возможно лишь на величину, равную или составляющую половину первоначального "недобора максимальных продаж"
на
рис. 5.5, в), оценку (5.53) можно принять для предприятия в целом. Следовательно, снижение продаж в соответствии с выражением (5.49) возможно лишь на величину, равную или составляющую половину первоначального "недобора максимальных продаж" 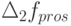 . С другой стороны, значение этого первоначального "недобора" не может составлять значительную часть от максимальных продаж
. С другой стороны, значение этого первоначального "недобора" не может составлять значительную часть от максимальных продаж 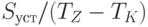 по причине близости точки "1" к вершине треугольника (см.
рис. 5.7).
по причине близости точки "1" к вершине треугольника (см.
рис. 5.7).
Окончательный вывод: резкое, "ступенчатое" снижение продаж в момент 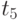 без возникновения дефицита денежных средств возможно лишь на незначительную величину, тогда как реальные падения рынка в связи с сезонными факторами могут быть существенно б?льшими. Следовательно, функционирование предприятия на участке 4 с некоторым запасом денежных средств (составляющих, исходя из практически известной оценки, единицы процентов от обязательств) приводит к неприемлемо высокому риску. Снижение риска возможно, если увеличить запас денежных средств на участке 4, т. е. отказаться от нахождения начальной точки "1" вблизи точки максимальных продаж. Однако этот путь означает снижение продаж.
без возникновения дефицита денежных средств возможно лишь на незначительную величину, тогда как реальные падения рынка в связи с сезонными факторами могут быть существенно б?льшими. Следовательно, функционирование предприятия на участке 4 с некоторым запасом денежных средств (составляющих, исходя из практически известной оценки, единицы процентов от обязательств) приводит к неприемлемо высокому риску. Снижение риска возможно, если увеличить запас денежных средств на участке 4, т. е. отказаться от нахождения начальной точки "1" вблизи точки максимальных продаж. Однако этот путь означает снижение продаж.
Нами предложен и разработан иной путь решения проблемы, состоящий в заблаговременном и постепенном снижении продаж до момента 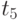 падения рынка. Достоинство этого пути в том, что потери продаж могут иметь место лишь на части участка 4, тогда как на другой части продажи могут находиться вблизи максимальных. Очевидно, этот путь приемлем, лишь поскольку возможно прогнозирование момента падения рынка, в частности, в связи с сезонными факторами.
падения рынка. Достоинство этого пути в том, что потери продаж могут иметь место лишь на части участка 4, тогда как на другой части продажи могут находиться вблизи максимальных. Очевидно, этот путь приемлем, лишь поскольку возможно прогнозирование момента падения рынка, в частности, в связи с сезонными факторами.
Возможность заблаговременного и постепенного снижения продаж существует, поскольку состояние предприятия в точке "3" подобно состоянию в точке "1". Поэтому из точки "3" может быть реализована аналогичная последовательность управлений потоками, которая вывела предприятие из исходного состояния (см. рис. 5.7, в). При этом величина "шагов" последовательно нарастает. Из нового состояния последовательность управлений при необходимости может быть повторена еще раз, и так до тех пор, пока продажи не снизятся до необходимого уровня. Характер уменьшения продаж со временем ( рис. 5.8) напоминает лестницу с увеличивающимися шириной и высотой ступеней.
Для реализации такого ступенчатого управления синхронное уменьшение продаж и поставок должно осуществляться искусственно, в противоположность процессам, изображенным на
рис. 5.7, а, где продажи уменьшались вынужденно под влиянием падения рынка. При достаточно большой продолжительности участка 4 снижение продаж в момент 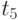 может быть любым вплоть до нулевой величины. Можно ожидать, что время, необходимое для заблаговременного постепенного снижения продаж, увеличивается с уменьшением начального запаса денежных средств, так как увеличивается число "ступеней лестницы".
может быть любым вплоть до нулевой величины. Можно ожидать, что время, необходимое для заблаговременного постепенного снижения продаж, увеличивается с уменьшением начального запаса денежных средств, так как увеличивается число "ступеней лестницы".
Следовательно, анализ управления потоками по типу "лестницы" выявляет принципиальную возможность функционирования предприятия в условиях существенного резкого падения рынка с частичным сохранением продаж вблизи максимума на предшествующем участке повышенного спроса, где ограничивающим продажи фактором является ограниченность источников средств. Для этого продолжительность участка повышенного спроса должна быть достаточно велика. Очевидно, желательно сократить потери продаж на участке повышенного рынка, для чего желательно уменьшать длину "лестницы", а точнее, уменьшать площадь между траекторией "лестницы" (см. рис. 5.8) и линией максимальных продаж.
Таким образом, возникает вопрос об улучшении управления по типу "лестницы". Например, постепенное снижение продаж может быть плавным, а не ступенчатым. Действительно, сделанный анализ показывает возможность реализовать постепенное снижение продаж в некоторых условиях, но не дает оснований считать управление по типу "лестницы" наилучшим, т. е. обеспечивающим максимум продаж.
В настоящей лекции этот вопрос изучается путем постановки, решения и исследования задачи оптимального планирования деятельности простейшего предприятия в условиях известного изменения рынка, в частности, когда определяемые спросом максимальные продажи  скачкообразно изменяются от достаточно больших значений до величин, ограничивающих возможный сбыт. Для решения такой оптимизационной задачи применяющиеся выше графоаналитические методы непригодны, и поэтому необходимо применение численных методов. Применение метода динамического программирования затрудняется значительным количеством возможных состояний простейшего предприятия, соответственно, высокой размерностью задачи. Поэтому в настоящей лекции разрабатывается метод, ориентированный на решение задачи краткосрочного планирования предприятий, реализующий управление системами внутрипроизводственных потоков и специально приспособленный для быстрого и удобного получения оптимальных решений, что позволило ниже выполнить их исследование.
скачкообразно изменяются от достаточно больших значений до величин, ограничивающих возможный сбыт. Для решения такой оптимизационной задачи применяющиеся выше графоаналитические методы непригодны, и поэтому необходимо применение численных методов. Применение метода динамического программирования затрудняется значительным количеством возможных состояний простейшего предприятия, соответственно, высокой размерностью задачи. Поэтому в настоящей лекции разрабатывается метод, ориентированный на решение задачи краткосрочного планирования предприятий, реализующий управление системами внутрипроизводственных потоков и специально приспособленный для быстрого и удобного получения оптимальных решений, что позволило ниже выполнить их исследование.