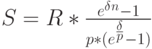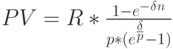Временная стоимость денег

Из таблицы видно, что при альтернативных затратах 20% сегодняшняя стоимость будущих доходов составляет 8,98 тыс. руб. Именно эта величина и должна сравниваться с инвестициями для определения целесообразности принятия проекта или отказа от его реализации. Обобщая алгоритм, по которому выполнялись расчеты, получаем общую формулу дисконтирования денежных потоков:

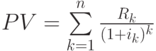( 3)

Так как в нашем примере и постоянные величины, то снова применяя правило суммирования геометрической прогрессии, получим частную формулу дисконтирования аннуитета:

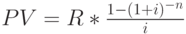( 4)

Второй сомножитель этого выражения – – называется дисконтным множителем аннуитета.

Формулы (3) и (4) описывают наиболее общие случаи наращения и дисконтирования аннуитетов: рассматриваются только ограниченные ренты, выплаты и начисление процентов производятся 1 раз в году, используется только эффективная процентная ставка . Так же как и в случае единичных сумм все эти параметры могут меняться. Поэтому существуют модифицированные формулы наращения и дисконтирования аннуитетов, учитывающие особенности отдельных денежных потоков. Основные из них, относящиеся к ограниченным денежным потокам, представлены в табл. 2.6

Таблица 2.6. Основные формулы наращения и дисконтирования ограниченных аннуитетов

Виды рент	Наращение	Дисконтирование
Годовая с начислением несколько раз в году ( )	( 5)	( 11)
p-срочная с начислением 1 раз в году ( )	( 6)	( 12)
p- срочная с начислением несколько раз в году ( )	( 7)	( 13)
p- срочная с начислением несколько раз в году ( )	( 8)	( 14)
Годовая с начислением непрерывных процентов ( )	( 9)	( 15)
p-срочная с начислением непрерывных процентов ( )	( 10)	( 16)

В табл. 2.6 не нашли отражения формулы расчета неограниченных денежных потоков, т.е. вечных рент или перпетуитетов. Существуют финансовые инструменты, предполагающие бессрочную выплату доходов их держателям. Одним из примеров таких ценных бумаг являются т.н. консоли (консолидированные ренты), эмитируемые британским казначейством начиная с XVIII века. В случае смерти владельца они передаются по наследству, обеспечивая тем самым действительную "бесконечность" денежного потока. Очевидно, что будущую стоимость ренты такого рода определить невозможно – ее сумма также будет стремиться к бесконечности, однако приведенная величина вечного денежного потока может быть выражена действительным числом. Причем, формула ее определения очень проста:

( 17)

где – член ренты (разовый платеж),

– сложная процентная ставка.

Например, по условиям страхового договора компания обязуется выплачивать 5 тыс. рублей в год на протяжении неограниченного периода, т.е. вечно. Чему должна быть равна стоимость этого перпетуитета, если уровень процентной ставки составит 25% годовых? В соответствии с (17) текущая стоимость всех предстоящих платежей по договору будет равна 20 тыс. рублей (5 / 0,25).

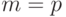Если неограниченная рента выплачивается раз в году, и начисление процентов по ней производится раз за год, причем , то формула расчета ее приведенной стоимости принимает вид:

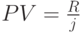( 18)

где – номинальная процентная ставка.

Предположим, рассмотренный выше перпетуитет будет выплачиваться дважды в год по 2,5 тыс. рублей, столько же раз будут начисляться проценты (25% в этих условиях становится номинальной ставкой). Его стоимость останется неизменной 20 тыс. рублей ((2,5 + 2,5) / 0,25).

В наиболее общем виде ( ) формула приведенной стоимости перпетуитета записывается следующим образом:

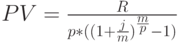( 19)

В принципе, ее можно использовать во всех случаях, подставляя соответствующие значения параметров 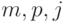, или . Если предположить четырехразовое начисление процентов по рассматриваемому перпетуитету, то в соответствии с (19) его текущая стоимость составит:

.

Интересно отметить связь существующую между годовой вечной и годовой ограниченной рентами ( аннуитетами ). Преобразовав правую часть формулы (4), получим:

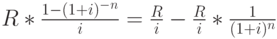( 20)

То есть современная величина конечной ренты, имеющей срок периодов, может быть представлена как разница между современными величинами двух вечных рент, выплаты по одной из которых начинаются с первого периода, а по второй – с периода ( ).

В случае, если член вечной ренты ежегодно увеличивается с постоянным темпом прироста , то приведенная стоимость такой ренты определяется по формуле:

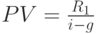( 21)

где 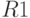– член ренты в 1-м году.

Данная формула имеет смысл при 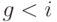. Она применяется в оценке обыкновенных акций.

При сравнении приведенной стоимости различных аннуитетов можно избежать громоздких вычислений, запомнив следующее правило: увеличение числа выплат по ренте в течение года ( ) увеличивает ее текущую стоимость, увеличение числа начислений процентов (m), наоборот, уменьшает. При заданных значениях 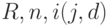наиболее высокий результат даст дисконтирование p-срочной ренты с 1 начислением процентов в год ( 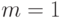). Самый низкий результат при этих же условиях будет получен по годовой ренте ( ) с непрерывным начислением процентов. По мере увеличения современная величина ренты будет расти, по мере роста она будет снижаться. Причем изменение дает относительно больший результат, чем изменение . То есть любая p-срочная рента даже с непрерывным начислением процентов ( 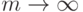) будет стоить дороже, чем годовая рента ( ) с 1 начислением процентов в год ( 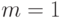). Например, по облигации предусмотрена ежегодная выплата 1 тыс. рублей в течение 5 лет. Процентная ставка составляет 20%. При начислении декурсивных процентов 1 раз в год стоимость этой ренты по базовой формуле (4) составит 2,99 тыс. рублей. Если выплаты будут производиться 2 раза в год по 500 рублей, то по формуле (12) стоимость ренты будет равна уже 3,13 тыс. рублей. Но если по последнему варианту начислять проценты 2 раза в год (13), текущая величина ренты снизится до 3,07 тыс. рублей. Если же двукратное начисление применить к исходному варианту при (11), то приведенная стоимость ренты станет еще меньше 2,93 тыс. рублей. Самым дешевым будет вариант годовой ренты ( ) с непрерывным начислением процентов (15) – 2,86 тыс. рублей.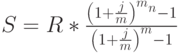
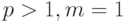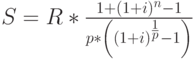
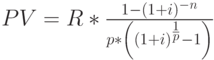
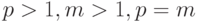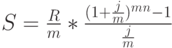
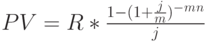
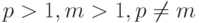
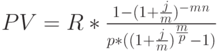
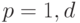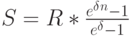
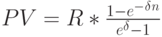