Технология баз информации. Информационное обеспечение процессов управления в экономике
7.5. Базы знаний и их применение для формирования экономических решений
7.5.1. Модели представления знаний
Знания, также как и данные, являются информационным ресурсом и хранятся в компьютере в соответствии с разработанной моделью.
База знаний – это знания человека (эксперта, специалиста), помёщенные в память компьютера в соответствии с некоторой моделью.
Работа с базами знаний – это одно из направлений искусственного интеллекта, целью которого является создание инструментальных средств, позволяющих решать задачи, традиционно считающиеся интеллектуальными.
Модель - это правила или соглашения, выполнение которых позволяет представить нечто в памяти компьютера в том виде, которая позволяет использовать формальные (программные) средства для их обработки (получение новых знаний).
Существуют различные модели представления баз знаний, среди которых в экономике наиболее популярными являются (рис.7.15):
Так как любая модель, и в том числе модель представления знаний, формальна, поэтому могут создаваться программные средства для их обработки.
Знания, как и прочие формы представления информации, устаревают или становятся ненужными, поэтому должна быть система управления ими. Управление знаниями - это совокупность программных средств, обеспечивающих поиск, ввод, обработку, использование и корректировку знаний.
7.5.2. Деревья (вывода, целей)
Дерево вывода. Дерево вывода — это множество объединённых правил, отражающих условия выполнения некоторого процесса. Правила представляют собой языковую конструкцию вида
ЕСЛИ <условие, сt(условия)>, ТО <заключение, сt(заключения)>
сt (правила),
где сt (условия), сt (заключения), сt (правила) – соответственно, коэффициенты определённости условия, заключения и правила.
Значение ct, равное 0, указывает на полную неопределённость, а 1 — на полную определённость. В дереве указывают значения в этом диапазоне.
Множество правил объединяются в дерево вывода.
Пример. Пусть заданы два правила.
Правило 1. ЕСЛИ индекс цен возрастет не менее чем на 3% (В) ct(B)
И цены на энергоносители вырастут не более чем на 19% (С) ct(C) = 0,6,
ТО акции покупать (A) ct(A) = ?, сt (правила 1) = 0,8.
Правило 2. ЕСЛИ ВВП возрастет не менее чем на 1,5% (Д) ct (Д) = 0,4,
ИЛИ ставки Центрального банка будут в пределах 12% (Е) ct(E) = 0,7,
ИЛИ объём экспорта возрастет более чем на 5% (G) ct(G) = 0,5,
ТО индекс цен возрастёт менее чем на 3%. (В) ct(B) - ?, ct (правила 2) = 0,98.
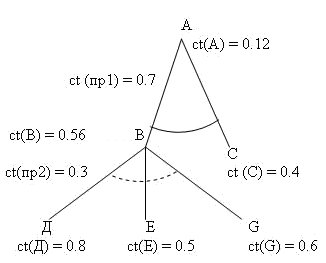
Эти правила объединяются в дерево (рис.7.16).
Рассмотрим, как знания такого рода представляются графически, а также как рассчитывается коэффициент определённости выводов. Правило с одним условием вида ЕСЛИ А, ТО В графически представляется следующим образом:

Здесь А — это условие, В — заключение. Далее условимся заключение, получаемое с помощью правила, изображать сверху, а условия — снизу. Число рядом с условием указывает на его определённость, а число рядом с линией — на определённость самого правила.
В правиле может быть несколько условий, связанных между собой союзами И или ИЛИ. Например,
ЕСЛИ А и В и С, ТО Е;
ЕСЛИ А или В или С, ТО Е.
Графически эти правила представлены на рис.7.17.
Сплошная или пунктирная дуга указывает на вид объединения условий: союзом И или союзом ИЛИ, соответственно. Число, указанное рядом с дугой (сплошной или пунктирной), указывает на определённость правила, а числа рядом с условиями — на определённость условий. Лицо, принимающее решение, присваивает условиям (А, В, С) и правилу некоторый коэффициент определённости от 0 до 1.
С помощью специальных формул рассчитывается коэффициент определённости для заключения. Для простого правила, содержащего лишь одно условие, например ЕСЛИ Е, ТО С, коэффициент определённости для заключения С рассчитывается так:
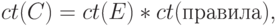
где ct (C), ct (E) и ct (правила) — коэффициенты определённости, соответственно, заключения С, условия Е и правила.
Например, при ct (E) = 0,4; ct (правила) = 0,2 коэффициент определённости заключения равен ct (C) = 0,08.
Если в правиле несколько условий, связанных союзом И, то для расчёта коэффициента определённости заключения применяется следующая операция:
ЕСЛИ (Е1 и Е2), ТО С.
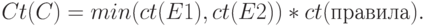
Для правила, в котором присутствует несколько условий, связанных связкой ИЛИ, применяется операция вида:
ЕСЛИ (Е1 или Е2), ТО С.
ct(C) = max(ct(E1), ct(E2)) ct (правила).
Например, ЕСЛИ (El и Е2),ТО С. При ct(El) = 0,7; ct(E2) = 0,6; ct(npaвилa) = 0,8; ct (условия) = min(0,7; 0,6) = 0,6 коэффициент определённости заключения равен ct(C) = 0,6 * 0,8 = 0,48.
Для заключения А, вывод которого представлен на рис.7.15, при ct (Д) = 0,8; ct(E) = 0,5; ct(G) = 0,6; ct(npl) = 0,7; ct(C) = 0,4; ct(np2) = 0,3 его коэффициент определённости А равен ct(A) = = 0,12.
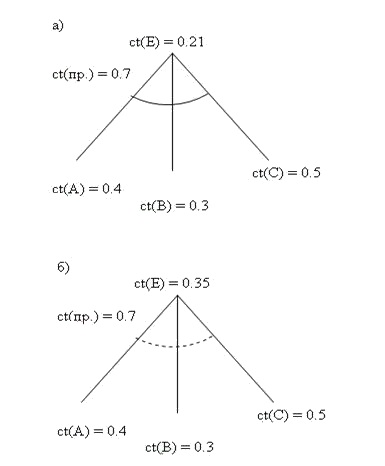
Рис. 7.17. Графическое представление правил: а – условия связаны союзом И; б – условия связаны союзом ИЛИ
Дерево целей. Дерево целей и задач — развёрнутая, распределённая по уровням совокупность целей и задач экономической программы, построенная по логической схеме:
"цели — программы — задачи, которые надо решить для достижения этих целей, - мероприятия, обеспечивающие решение задач, — ресурсы, необходимые для проведения мероприятий".
Дерево целей и задач используется в программно-целевом планировании и управлении при разработке целевых комплексных программ.
Дерево целей является дальнейшим совершенствованием целевого управления, известного в настоящее время как Goal-управление.
В основу его построения положено понятие цели, измерение достижения которой осуществляется с помощью значений соответствующих экономических показателей.
Например, уровень достижения цели "Увеличить рентабельность предприятия" можно измерить показателем "Рентабельность" в числовом диапазоне от 0 до 1.
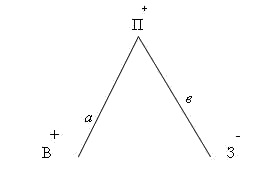
Представление знаний в виде дерева целей возможно, если известны цель управления и формулы, по которым можно рассчитать уровень достижения каждой подцели. Допустим, целью является увеличение прибыли, которая может быть достигнута за счёт увеличения выручки и снижения затрат, что можно представить графически (рис.7.18).
На рис.7.18 с помощью знаков "+" и "-" показаны желаемые направления изменения подцелей: В — выручка: увеличение; 3— затраты: снижение; П— прибыль: увеличение. Если В = 20, 3= 15, то по формуле В = П— 3 получим П= 5.
Используется дерево целей следующим образом: допустим, необходимо поднять прибыль до 7 ед. Для этого нужно установить приоритеты в достижении данной цели, чему служат коэффициенты  и
и  . Сумма этих коэффициентов всегда равна 1.
. Сумма этих коэффициентов всегда равна 1.
Дерево целей можно продолжить, если указать, из чего состоят выручка и затраты. Это позволит рассчитать управляющие воздействия более детального характера.