|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Цифровая подпись
Схема цифровой подписи Эль-Гамаля
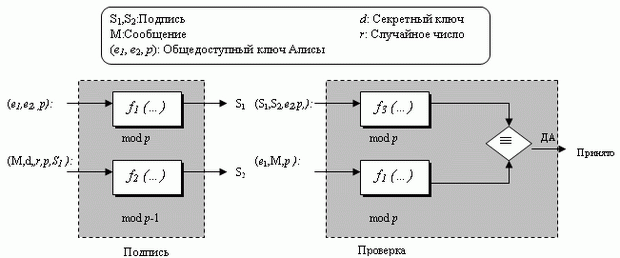
Криптосистема Эль-Гамаля была обсуждена в "B. Стандарты и организации по стандартизации" . Схема цифровой подписи Эль-Гамаля использует те же самые ключи, но алгоритм различен. рис. 3.9 дает общую идею схемы цифровой подписи Эль-Гамаля.
В процессе подписания две функции создают две подписи. На стороне подтверждения обрабатывают выходы двух функций и сравнивают между собой для проверки. Обратите внимание, что одна и та же функция применяется и для подписания, и для проверки, но использует различные входы. Рисунок показывает входы каждой функции. Сообщение - часть входа, для обеспечения функционирования при подписании; оно же - часть входа к функции 1 при подтверждении. Обратите внимание, что вычисления в функциях 1 и 3 проводятся по модулю p, а функции 2 - по модулю p - 1.
Генерация ключей
Процедура генерации ключей здесь точно такая же, как та, которая используется в криптографической системе. Выберем достаточно большое простое число p, чтобы в поле Z p* проблема дискретного логарифма была достаточно трудной. Пусть e1 - простой элемент в Z p*. Алиса выбирает свой секретный ключ d, чтобы он был меньше, чем p - 1. Она вычисляет e2 = e1d. Открытый ключ Алисы - кортеж (e1, e2, p) ; секретный ключ Алисы - d.
Подтверждение и проверка
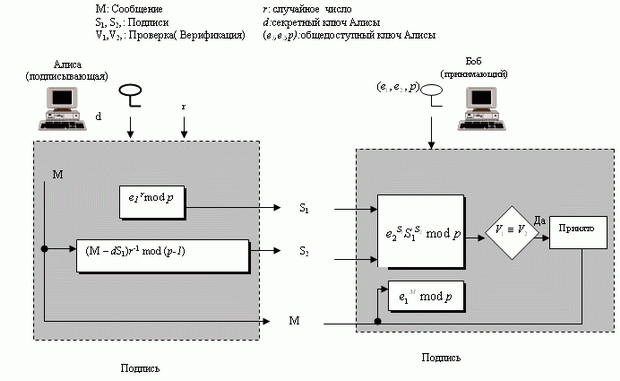
Рисунок 3.10 показывает схему цифровой подписи Эль-Гамаля.
Подписывающаяся Алиса может подписать дайджест сообщения, направленный к любому объекту, включая Боба.
- Алиса выбирает секретное случайное число r. Обратите внимание, что хотя открытые и секретные ключи могут использоваться неоднократно, Алиса каждый раз нуждается в новом r, когда она подписывает новое сообщение.
- Алиса вычисляет первую подпись S1 = er mod p.
- Алиса вычисляет вторую подпись S2 = (М - d x S1) x r-1 mod (p - 1),где r - мультипликативная инверсия r по модулю p - 1.
- Алиса передает М, S1 и S2 Бобу.
Проверка. Объект, например Боб, получает М, S1 и S2 и может проверить их следующим образом.
- Боб проверяет, что 0 < S1 < p.
- Боб проверяет, что 0 < S2 < p - 1.
- Боб вычисляет V1 = e1M mod p.
- Боб вычисляет V2 = e2S1 x e2S2 mod p.
- Если V1 является конгруэнтным V2, сообщение принято; иначе оно будет отклонено. Мы можем доказать правильность этого критерия проверки, используя e2 = e1d и S1 = e1r:

Мы имеем

Поскольку e1 - первообразный корень, может быть доказано, что вышеупомянутое сравнение справедливо тогда и только тогда, когда
![M \equiv [dS_{1} + rS_{2}] mod \ (p-1) S_{2} \equiv [(M - d \times S_{1}) \times r^{-1}] mod \ (p-1)](/sites/default/files/tex_cache/c64acf12b770b82d8b9c7d7790d938a7.png) , и результат сравнения есть тот же самый S2, с которого мы начали процесс подписания.
, и результат сравнения есть тот же самый S2, с которого мы начали процесс подписания.
Пример 3.2
Ниже приводится тривиальный пример. Алиса выбрала p = 3119, e1 = 2, d = 127 и вычислила e2 = 2127 mod 3119 = 1702. Она выбрала r равным 307. Она объявила e1, e2 и p ; она сохранила в тайне d. Далее показано, как Алиса может подписать сообщение.
M = 320 S1 = e1r = 2307 = mod3119 S2 = (M - d x S1) x r-1 = (320 - 127 x 2083) x 307-1 = 2105 mod 3118
Алиса передает М, S1 и S2 Бобу. Боб использует открытый ключ, чтобы вычислить, что сообщение подписано Алисой, потому что никто, кроме Алисы, не имеет секретного ключа d.
V1 = e1M = 2320 = 3006 mod 3119 V2 = dS1 x S2S1 = 17022083 x 20832105 = 3006 mod 3119
Поскольку V1 и V2 являются конгруэнтными, Боб принимает сообщение, и он предполагает, что сообщение было подписано Алисой, потому что никто, кроме нее, не имеет секретного ключа Алисы d.
Пример 3.3
Теперь вообразите, что Алиса хочет передать другое сообщение, М = 3000, Тэду. Она выбирает новое r = 107. Алиса передает М., S1 и S2 Тэду. Тэд использует общедоступные ключи, чтобы вычислить V1 и V2.
M = 3000 S1 = e1r = 2107 = 2732mod3119 S2 = (M - d x S1) x r-1 = (3000 - 127 x 2083) x 107-1 = 2526 mod 3118 V1 = e1M = 23000 = 704 mod 3119 V2 = dS1 x S1S2 = 17022732 x 20832526 = 704 mod 3119
Поскольку V1 и V2 являются конгруэнтными, Тэд принимает сообщение; он предполагает, что сообщение подписано Алисой, потому что никто, кроме нее, не имеет секретного ключа Алисы d. Обратите внимание, что сообщение может получить любой человек. Цель состоит не в том, чтобы скрыть сообщение, но в том, чтобы доказать, что его передает Алиса.
Подделка цифровой подписи в схеме Эль-Гамаля
Схема цифровой подписи Эль-Гамаля уязвима к экзистенциальной подделке, но селективную подделку на этой схеме сделать очень трудно.
Подделка только ключа. В этом типе подделки Ева имеет доступ только к открытому ключу. Возможны два варианта:
- Ева имеет заранее заданное сообщение М. Она должна подделать подпись Алисы на этом сообщении. Ева должна найти две правильных подписи S1 и S2 для этого сообщения. Это - селективная подделка.
- Ева может методом случайного подбора найти три значения, М, S1 и S2, такие, что подпись первого используется для второго. Если Ева может найти два новых параметра x и y, такие, что М = xS2 mod (p - 1) и S1 = -y S2 mod (p - 1), то она может подделать сообщение, но серьезной выгоды не получит, поскольку это - экзистенциальная подделка.
Подделка при известном сообщении. Если Ева перехватила сообщение М и его две подписи S1 и S2, она может найти другое сообщение М', с той же самой парой подписей S1 и S2. Однако обратите внимание, что это - экзистенциальная подделка, которая не помогает Еве.


 . Другими словами,
. Другими словами, 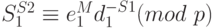 или
или 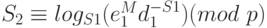 . Это
означает
вычисление
. Это
означает
вычисление