|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Преобразования
9.2. Преобразования
Чтобы обеспечить безопасность, AES использует четыре типа преобразований: подстановка, перестановка, смешивание и добавление ключа. Ниже мы обсудим каждое.
Подстановка
AES подобно DES использует подстановку. Однако этот механизм имеет различия. Первое: подстановка делается для каждого байта. Второе: для преобразования каждого байта используется только одна таблица — это означает, что если два байта одинаковы, то и результат преобразования одинаков. Третье: преобразование определяется или процессом поиска в таблице, или математическим вычислением в GF(28) поле. AES работает с двумя обратимыми преобразованиями.
SubBytes
Первое преобразование, SubBytes, используется на стороне шифрования. Чтобы применить подстановку к байту, мы интерпретируем байт как две шестнадцатеричные цифры. Левая цифра определяет строку, а правая — колонку в таблице перестановки. На пересечении строки и колонки, обозначенных этими шестнадцатеричными цифрами, находится новый байт. Рисунок 9.6 иллюстрирует идею.
В преобразовании SubBytes состояние обрабатывается как матрица байтов
 . В один момент проводится преобразование одного байта. Содержание каждого байта изменяется, но расположение байтов в матрице остается тем же самым. В процессе преобразования каждый байт преобразуется независимо от других — это шестнадцать личных преобразований байт в байт.
. В один момент проводится преобразование одного байта. Содержание каждого байта изменяется, но расположение байтов в матрице остается тем же самым. В процессе преобразования каждый байт преобразуется независимо от других — это шестнадцать личных преобразований байт в байт.
Таблица 9.1 показывает таблицу подстановки (S-блок) для преобразования SubBytes. Преобразование обеспечивает эффект перемешивания. Например, два байта, 5A16 и 5B16, которые отличаются только одним битом (самый правый бит), преобразованы в BE16 и 3916, которые отличаются четырьмя битами.
InvSubBytes
InvSubBytes — инверсия SubBytes. Преобразование сделано с использованием таблицы 9.2, и мы можем легко проверить, что эти два преобразования являются обратными друг другу.
Пример 9.2
Рисунок 9.7 показывает, как матрица состояний преобразуется с использованием SubBytes. Рисунок также показывает, что InvSubBytes однозначно воспроизводит оригинал. Заметим, что если два байта имеют одинаковое значение, то они преобразуются одинаково. Например, два байта 0416 и 0416 в левой матрице состояний преобразуются в F216 и F216 в правой матрице состояний и наоборот. Причина в том, что каждый байт использует одну и ту же таблицу преобразований.
Преобразование с использованием поля GF(2 в степени 8)
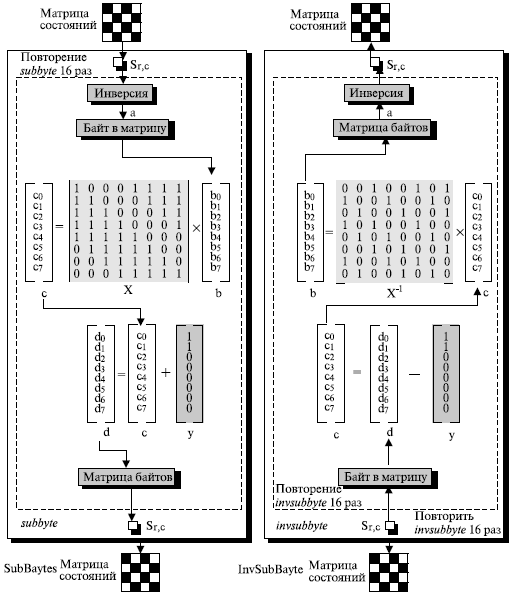
Хотя мы можем использовать таблицы 9.1 и 9.2 для перестановки каждого байта, AES дает определение алгебраическим преобразованиям на основе поля GF(28) с помощью неприводимых полиномов (x8 + x4 + x3 + x + 1), как это показано на рис. 9.8.
Преобразование SubByte повторяет процесс, называемый subbyte, шестнадцать раз. Inv SubByte повторяет процесс, называемый invsubbyte. Каждый шаг преобразования обрабатывает один байт.
В процедуре subbyte байт (двоичной строки на 8 битов) находится в GF(28) с помощью неприводимого полинома по модулю (x8 + x4 + x3+ x + 1). Обратите внимание, что байт — 0016 сам является собственной инверсией. Инвертированный байт затем интерпретируется как матрица-столбец с самым младшим битом наверху и самым старшим битом внизу. Эта матрица-столбец умножается на постоянную квадратную матрицу, X, и результат, который является матрицей-столбцом, складывается с постоянной матрицей столбца y, что дает новый байт. Обратите внимание, что умножение и сложение битов происходит в GF(2). invsubbyte делает те же самые действия в обратном порядке.
После нахождения байта инверсного сомножителя процесс похож на аффинное шифрование, которое мы обсуждали в "Традиционные шифры с симметричным ключом" . При шифровании умножение является первой операцией, сложение — второй. При дешифровании вычитание (сложение инверсией) является первым, а деление (умножение с инверсией) — вторым. Мы можем легко доказать, что эти два преобразования инверсны друг другу, потому что сложение или вычитание в GF(2) — фактически операция ИСКЛЮЧАЮЩЕЕ ИЛИ.
Пример 9.3
Покажем, как байт 0C преобразуется в FE с помощью процедуры subbyte и преобразуется обратно в 0C с помощью процесса invsubbyte.
a. Инверсный сомножитель в поле GF(28) есть B0 или в двоичном отображении b (1011 0000).
b. Умножая на матрицу X эту матрицу, имеем в результате c = (10011101).
c. Результат применения операции XOR (ИСКЛЮЧАЮЩЕЕ ИЛИ ) - d = (11111110) FE в шестнадцатеричном представлении.
2. invsubbyte
a. Результат применения операции XOR (ИСКЛЮЧАЮЩЕЕ ИЛИ) - c = (10011101)
b. Результат умножения на матрицу X~1 - (11010000) или B0.
c. Инверсия по умножению B0 - это 0C.
Алгоритм
Хотя на рисунке мы показали матрицы, чтобы подчеркнуть характер подстановки (аффинное преобразование), алгоритм не обязательно использует умножение и сложение матриц, потому что большинство элементов в постоянной квадратной матрице — только 0 или 1. Значение постоянной матрицы столбца —  . Мы можем написать простой алгоритм, чтобы выполнить SubByte. Алгоритм 9.1 вызывает процедуру subbyte 16 раз — один раз для каждого байта в матрице состояний. Процедура ByteToMatrix преобразовывает байт к матрицу-столбец
. Мы можем написать простой алгоритм, чтобы выполнить SubByte. Алгоритм 9.1 вызывает процедуру subbyte 16 раз — один раз для каждого байта в матрице состояний. Процедура ByteToMatrix преобразовывает байт к матрицу-столбец  . Процедура MatrixToByte преобразовывает матрицу-столбец
. Процедура MatrixToByte преобразовывает матрицу-столбец  к байту. Расширение этого алгоритма для InvSubBytes оставляем как упражнение.
к байту. Расширение этого алгоритма для InvSubBytes оставляем как упражнение.
Нелинейность
Хотя умножение и сложение матриц в процедуре subbyte — преобразование аффинного типа и линейно, замена байта его мультипликативной инверсией в GF(28) — нелинейная. Этот шаг делает все преобразование нелинейным.




![\tt\parindent0pt
\
subbyte:
d = X (s_{r,c})^{-1} \oplus y
invsubbyte:
$[X^{-1} (d \oplus y)^{-1}] = [X^{-1} (X ((s_{r,c})^{-1}y\oplus y]^{-1} = [(s_{r,c})^{-1}]^{-1} = s_{r,c}$](/sites/default/files/tex_cache/b5d099bb333e281e0f14b31177c08478.png)