|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Алгебраические структуры
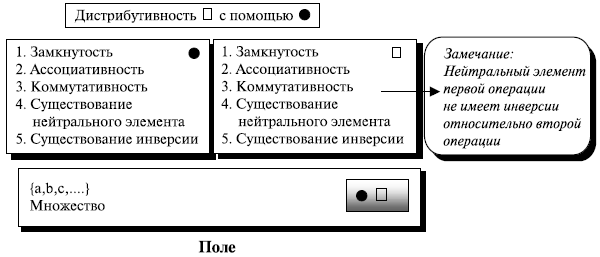
Поле
Поле, обозначенное 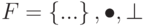 — коммутативное кольцо, в котором вторая операция удовлетворяет всем пяти свойствам, определенным для первой операции, за исключением того, что нейтральный элемент первой операции (иногда называемый нулевой элемент) не имеет инверсии. Рисунок 5.5 показывает поле.
— коммутативное кольцо, в котором вторая операция удовлетворяет всем пяти свойствам, определенным для первой операции, за исключением того, что нейтральный элемент первой операции (иногда называемый нулевой элемент) не имеет инверсии. Рисунок 5.5 показывает поле.
Дополнительное замечание
Поле — структура, которая поддерживает две пары операций, используемые в математике: сложение/вычитание и умножение/деление. Есть одно исключение: не разрешено деление на нуль.
Конечные поля
Хотя общее определение касается полей бесконечного порядка, в криптографии используются экстенсивно только конечные поля. Конечное поле — поле с конечным числом элементов — является очень важной структурой в криптографии. Галуа показал что поля, чтобы быть конечными, должны иметь число элементов pn, где p — простое, а n — положительное целое число. Конечные поля обычно называют полями Галуа и обозначают как GF(pn).
Поля GF (p)
Когда n = 1, мы имеем поле GF (p). Это поле может быть множеством Zp, (0, 1, …p–1) с двумя арифметическими операциями (сложение и умножение). Любой элемент в этом множестве имеет аддитивную инверсию, и элементы, отличные от нуля, имеют мультипликативную инверсию (мультипликативная инверсия для 0 отсутствует).
Пример 5.12
Очень общее поле в этой категории — GF (2) с множеством {0,1} и двумя операциями, сложением и умножением, как показано на рисунке 5.6.
Есть несколько моментов, которые следует отметить в определении этого поля. Первый: множество имеет только два элемента, которые являются двоичными цифрами или битами ( 0 и 1 ). Второй: операция сложения — фактически ИСКЛЮЧАЮЩЕЕ ИЛИ ( XOR ), операция, которую мы используем с двумя двоичными цифрами. Третий: операция умножения — AND, операция, которую мы используем с двумя двоичными цифрами. Четвертый: сложение и операции вычитания — те же самые (операция XOR ). Пятый: умножение и операции деления — те же самые (ОПЕРАЦИЯ AND ).
Пример 5.13
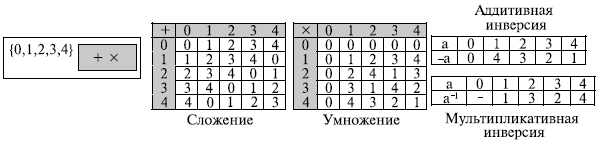
Мы можем определить GF(5) на множестве Z5 ( 5 простое) с операторами сложения и умножения, показанными на рис. 5.7.
Хотя мы можем использовать расширенный алгоритм Евклида, чтобы найти мультипликативные инверсии элементов в GF(5), проще составить таблицу умножения и находить каждую пару, произведение которой равняется 1. Это (1, 1), (2, 3), (3, 2) и (4, 4). Заметим, что мы можем на этом множестве применить вычитание и умножение/деление (за исключением запрещенного деления на 0 ).
Поля GF(p в степени n)
В дополнение к полям GF(p) в криптографии мы также интересуемся полями GF(pn). Однако множества Z, Zn, Zn* и Zp, которые мы использовали до сих пор с операциями сложения и умножения, не могут удовлетворить требованиям поля. Поэтому должны быть определены некоторые новые множества и некоторые новые операции на этих множествах. В следующей лекции мы рассматриваем очень полезное в криптографии поле GF(2n).
Итоги рассмотренных структур
Изучение трех алгебраических структур позволяет нам использовать множества, в которых могут применяться операции, подобные сложению/вычитанию и умножению/делению. Мы должны различать эти три структуры. Первая структура — группа, поддерживает одну пару связанных операций. Вторая структура — кольцо, поддерживает одну пару связанных операций и одну одиночную операцию. Третья структура — поле, поддерживает две пары операций. Таблица 5.3 может помочь нам увидеть эту разницу.