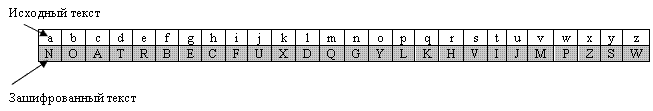|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Традиционные шифры с симметричным ключом
Мультипликативные шифры
В мультипликативном шифре алгоритм шифрования применяет умножение исходного текста ключом, а алгоритм дешифрования применяет деление зашифрованного текста ключом, как показано на рис. 4.10. Однако поскольку операции проводятся в Z26, дешифрование здесь означает умножение на мультипликативную инверсию ключа. Обратите внимание, что ключ должен принадлежать набору Zn* — это гарантирует, что шифрование и дешифрование инверсны друг другу.
Пример 4.7
Каково множество ключей для любого мультипликативного шифра?
Решение
Ключ должен быть в Z26*. Это множество имеет только 12 элементов: 1, 3, 5, 7, 9, 11, 15, 17, 19, 21, 23, 25.
Пример 4.8
Мы используем мультипликативный шифр, чтобы зашифровать сообщение "hello" с ключом 7. Зашифрованный текст "XCZZU".
Исходный текст h 07 Шифрование (07 x 07) mod 26 Шифр. Текст 23 X Исходный текст e 04 Шифрование (04 x 07) mod 26 Шифр. Текст 02 C Исходный текст l 11 Шифрование (11 x 07) mod 26 Шифр. Текст 25 Z Исходный текст l 11 Шифрование (11 x 07) mod 26 Шифр. Текст 25 Z Исходный текст o 14 Шифрование (14 x 07) mod 26 Шифр. Текст 20 U
Мы можем комбинировать аддитивные и мультипликативные шифры, чтобы получить то, что названо аффинным шифром — комбинацией обоих шифров с парой ключей. Первый ключ используется мультипликативным шифром, второй — аддитивным шифром. Рисунок 4.11 доказывает, что афинный шифр — фактически два шифра, применяемые один за другим. Мы могли бы показать только одну комплексную операцию для шифрования или дешифрования, такую, как  и
и  . Однако мы использовали временный результат ( T ) и указали две отдельных операции, показав тем самым, что всякий раз, когда мы используем комбинацию шифров, нужно убедиться, что каждый из них имеет инверсию на другой стороне линии и что они используются в обратном порядке в шифровании и дешифровании. Если сложение — последняя работа в шифровании, то вычитание должно быть первым в дешифровании.
. Однако мы использовали временный результат ( T ) и указали две отдельных операции, показав тем самым, что всякий раз, когда мы используем комбинацию шифров, нужно убедиться, что каждый из них имеет инверсию на другой стороне линии и что они используются в обратном порядке в шифровании и дешифровании. Если сложение — последняя работа в шифровании, то вычитание должно быть первым в дешифровании.
При аффинном шифре отношение между исходным текстом P и шифрованным текстом C определяется, как это показано ниже.
C = (P x k1 + k2 ) mod 26 P = ((C – k2) x k1-1) mod 26 где k1-1 мультипликативная инверсия k1, а(– k2)–аддитивная инверсия k2
Пример 4.9
Аффинный шифр использует пару ключей, в которой первый ключ из Z26*, а второй — из Z26. Область существования ключей равна  .
.
Пример 4.10
Используйте аффинный шифр, чтобы зашифровать сообщение "hello" с ключевой парой (7, 2).
Решение
Мы используем 7 для мультипликативного ключа и 2 для аддитивного ключа. Получаем "ZEBBW".
P: h 07 Шифрование (07 x 07+2) mod 26 C: 25 Z P: e 04 Шифрование (04 x 07+2) mod 26 C: 04 E P: l 11 Шифрование (11 x 07+2) mod 26 C: 01 B P: l 11 Шифрование (11 x 07+2) mod 26 C: 01 B P: o 14 Шифрование (14 x 07+2) mod 26 C: 22 W
Пример 4.11
Используйте аффинный шифр, чтобы расшифровать сообщение "ZEBBW" с ключевой парой (7, 2) в модуле 26.
Решение
Чтобы найти символы исходного текста, прибавим аддитивную инверсию от  к полученному зашифрованному тексту. Потом умножим результат на мультипликативную инверсию от
к полученному зашифрованному тексту. Потом умножим результат на мультипликативную инверсию от 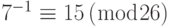 . Поскольку 2 имеет аддитивную инверсию в Z26 и 7 имеет мультипликативную инверсию в Z26*, исходный текст — точно тот, что мы использовали в примере 4.10.
. Поскольку 2 имеет аддитивную инверсию в Z26 и 7 имеет мультипликативную инверсию в Z26*, исходный текст — точно тот, что мы использовали в примере 4.10.
C: 25 -> Z Дешифрование (07 x 07 - 2) mod 26 P: 07 -> h C: 04 -> E Дешифрование (04 x 07 - 2) mod 26 P: 04 -> e C: 01 -> B Дешифрование (11 x 07 - 2) mod 26 P: 11 -> l C: 01 -> B Дешифрование (11 x 07 - 2) mod 26 P: 11 -> l C: 22 -> W Дешифрование (14 x 07 - 2) mod 26 P: 14 -> o
Пример 4.12
Аддитивный шифр — частный случай аффинного шифра, при котором k1 = 1. Мультипликативный шифр — частный случай аффинного шифра, в котором k2 = 0.
Криптоанализ аффинного шифра
Хотя методы грубой силы и статистический метод атаки могут использоваться только для зашифрованного текста, попробуем атаку с выборкой исходного текста. Предположим, что Ева перехватывает следующий зашифрованный текст:
PWUFFOGWCHFDWIWEJOUUNJORSMDWRHVCMWJUPVCCG
Ева также очень ненадолго получает доступ к компьютеру Алисы и время, достаточное лишь для того, чтобы напечатать исходный текст с двумя символами: "et". Тогда она пробует зашифровать короткий исходный текст, используя два различных алгоритма, потому что не уверена, какой из них является аффинным шифром.
Для того чтобы найти ключ, Ева использует следующую стратегию:
а. Ева знает, что если первый алгоритм является аффинным, она может составить следующие уравнения, основанные на первом наборе данных:
e -> W 04 -> 22 (04 x k1+k2) = 22 (mod 26) t- -> C 19 -> 02 (19 x k1+k2) = 02 (mod 26)
Как мы узнали в "Традиционные шифры с симметричным ключом" , эти два уравнения сравнения могут быть решены (могут быть найдены значения k1, и k2 ). Однако этот ответ неприемлем, потому что k1 = 16 не может быть первой частью ключа. Его значение, 16, не имеет мультипликативной инверсии в Z26*.
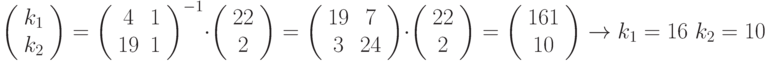
b. Ева теперь пробует использовать результат второго набора данных:
e -> W 04 -> 22 (04 x k1+k2) = 22 (mod 26) t- -> C 19 -> 05 (19 x k1+k2) = 05 (mod 26)
Квадратная матрица и ее инверсия — те же самые, что и в предыдущем примере. Теперь Ева получает k1 = 11 и k2 = 4, эта пара является приемлемой, потому что k1 имеет мультипликативную инверсию в Z26*. Она пробует пару ключей (19, 22), которые являются инверсией пары (11, 4), и расшифровывает сообщение. Исходный текст
Best time of the year is spring when flower bloom Самое лучшее время года — весна, когда цветут цветы
Моноалфавитный шифр подстановки
Поскольку аддитивные, мультипликативные и аффинные шифры имеют малое множество ключей, они очень уязвимы к атаке грубой силы. Алиса и Боб согласовали единственный ключ, который они используют, чтобы зашифровать каждую букву в исходном тексте или расшифровать каждую букву в зашифрованном тексте. Другими словами, ключ независим от передаваемых букв.
Лучшее решение состоит в том, чтобы создать отображение каждой буквы исходного текста на соответствующий символ зашифрованного текста. Алиса и Боб могут договориться об отображении для каждой буквы и записать его в виде таблицы. Рисунок 4.12 показывает пример такого отображения.
Пример 4.13
Мы можем использовать ключ, показанный на рисунке 4.12, чтобы зашифровать сообщение
This message is easy to encrypt but hard to find the key (это сообщение просто зашифровать, но трудно найти ключ, которым зашифрован текст)
Зашифрованное сообщение имеет вид
ICFVQRVVNEFVRNVSIYRGAHSLIOJICNHTIYBFGTICRXRS
Криптоанализ
Размер ключевого пространства для моноалфавитного шифра подстановки — число перестановок из 26, т.е. 26! (почти  ). Это делает атаку грубой силы чрезвычайно трудной для Евы, даже если она использует мощный компьютер. Однако она может применить статистическую атаку, основанную на частоте символов. Шифр не изменяет частоту употребления символов.
). Это делает атаку грубой силы чрезвычайно трудной для Евы, даже если она использует мощный компьютер. Однако она может применить статистическую атаку, основанную на частоте символов. Шифр не изменяет частоту употребления символов.