| Почему примере отношение t не транзитивно? |
Сочетания
Свойства сочетаний
-
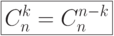
( 6.1) Первое свойство непосредственно вытекает из формул:
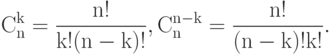
-
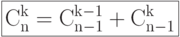
( 6.2) Доказательство:
Составим
 -элементные сочетания из
-элементные сочетания из  элементов
элементов 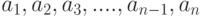 и разобьем их на два класса:
и разобьем их на два класса:1-й класс - сочетания, содержащие элемент
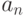 ;
;2-й класс - сочетания, не содержащие элемент
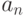 .
.Если из любого сочетания 1-го класса откинуть элемент
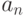 , то останется
, то останется  сочетание из
сочетание из  , их число
, их число  .
.Сочетания 2-го класса являются
 -элементными сочетаниями, составленными из
-элементными сочетаниями, составленными из  , их число
, их число 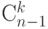 . Поскольку любое
. Поскольку любое  -элементное сочетание из
-элементное сочетание из 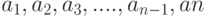 принадлежит одному и только одному из этих классов, а общее число равно
принадлежит одному и только одному из этих классов, а общее число равно 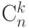 , то приходим к равенству (6.2).
, то приходим к равенству (6.2).Пример.
Пусть дано множество
 . Тогда
. Тогда 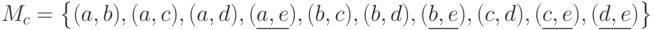 .
.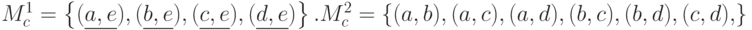 .
.С другой стороны,
 .
. 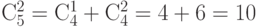 .
. -

( 6.3) Доказательство:
 - это число всех
- это число всех  размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в
размещений с повторениями из элементов двух типов. Разобьем эти размещения на классы, отнеся в  -й класс те, в которые входят
-й класс те, в которые входят  элементов 1-го типа и
элементов 1-го типа и 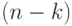 элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из
элементов 2-го типа. Размещения k-го класса - это не что иное, как всевозможные перестановки из  элементов 1-го типа и
элементов 1-го типа и 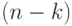 элементов 2-го типа. Мы знаем, что число таких перестановок равно
элементов 2-го типа. Мы знаем, что число таких перестановок равно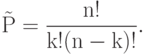
Вспомним формулу
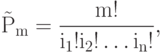
где
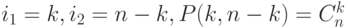 . Значит, общее число размещений всех классов равно
. Значит, общее число размещений всех классов равно  . С другой стороны, это же число равно
. С другой стороны, это же число равно  . Тем самым соотношение доказано.
. Тем самым соотношение доказано. -
Рассмотрим
 -элементные сочетания с повторениями, составленные из элементов
-элементные сочетания с повторениями, составленные из элементов  типов, скажем из
типов, скажем из  букв a, b, c,..., x. Число таких сочетаний равно
букв a, b, c,..., x. Число таких сочетаний равно
Разобьем все сочетания на классы, отнеся к
 -му классу сочетания, в которые
-му классу сочетания, в которые  раз входит буква
раз входит буква  , остальные
, остальные 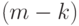 мест могут быть заняты оставшимися
мест могут быть заняты оставшимися  буквами с повторениями. Поэтому в
буквами с повторениями. Поэтому в  -й класс входит столько сочетаний, сколько можно составить
-й класс входит столько сочетаний, сколько можно составить 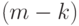 -элементных сочетаний с повторениями из элементов
-элементных сочетаний с повторениями из элементов  типов, т. е.
типов, т. е. 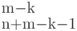 , значит, общее число всех сочетаний равно
, значит, общее число всех сочетаний равно 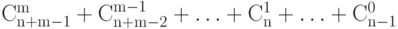 . С другой стороны, мы видим, что это число равно
. С другой стороны, мы видим, что это число равно  , т. е. утверждение доказано.
, т. е. утверждение доказано.
( 6.4) -
Заменяя
 на
на  и
и  на
на 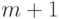 в соотношении (6.4), и помня, что
в соотношении (6.4), и помня, что  , получаем, что
, получаем, что
( 6.5) Частными случаями формулы (6.5) при
 являются следующие суммы рядов:
являются следующие суммы рядов:-
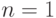 :
:
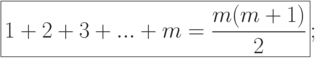
( 6.6) 
-
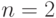 :
:
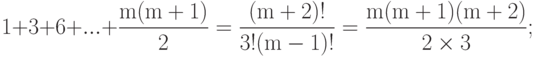
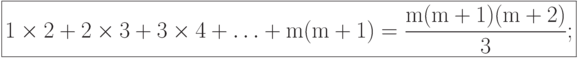
( 6.7) -
Аналогично для
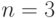 :
:
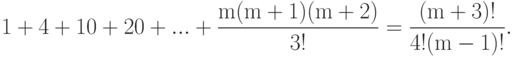
Следовательно,
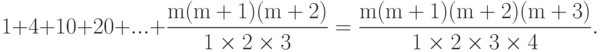
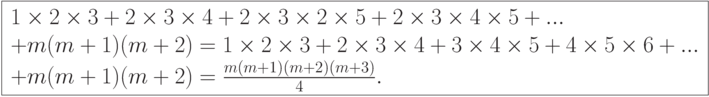
( 6.8) С помощью формулы (6.7) легко найти сумму квадратов натуральных чисел от
 до
до 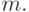
-
