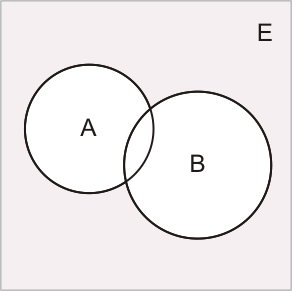
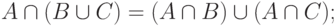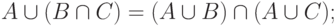| Почему примере отношение t не транзитивно? |
Алгебра множеств
Алгеброй  называется совокупность множества
называется совокупность множества  с заданными в нем операциями
с заданными в нем операциями 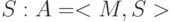 , где
, где  - носитель,
- носитель,  - сигнатура.
- сигнатура.
Алгеброй множеств  называется совокупность булеана универсального множества с заданными в нем операциями:
называется совокупность булеана универсального множества с заданными в нем операциями:

где 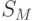 - множество операций: пересечение, объединение, дополнение, разность.
- множество операций: пересечение, объединение, дополнение, разность.
Законы алгебры множеств
Для операций объединения, пересечения и дополнения выполняются следующие законы:
-
коммутативности:
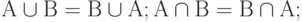
-
ассоциативности:

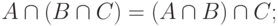
- дистрибутивности:
- идемпотентности:

- действия с универсальным и пустым множествами:
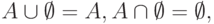

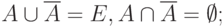
- де Моргана:


- двойного дополнения:
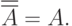
Доказательство законов можно выполнить графически или посредством последовательности утверждений типа "если  , то
, то  ", которое записывается как
", которое записывается как  .
.
Докажем закон дистрибутивности:
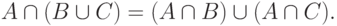
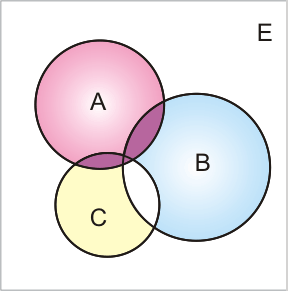
Графическое доказательство состоит в построении диаграмм Эйлера-Венна для правой и левой частей ( рис. 2.1).
Доказательство
Если  и
и 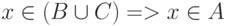 и
и 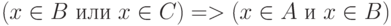 или
или 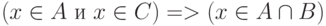 или
или  .
.
Таким образом, 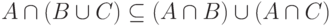 . Необходимо доказать включение в обратную сторону:
. Необходимо доказать включение в обратную сторону:
 или
или 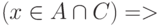
 или
или 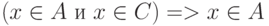 и
и  и
и 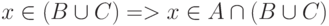 .
.
Следовательно, 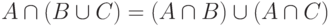 .
.

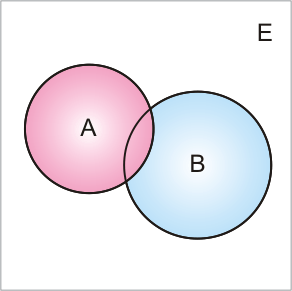
Графическая интерпретация представлена на рис. 2.2.
Рассмотрим графическую интерпретацию левой части закона де Моргана, в которой можно выделить три составные части ( рис. 2.3).
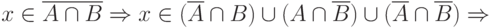
Используя закон идемпотентности ![\left[ х \cup х = х \right]}](/sites/default/files/tex_cache/3930c4e8f34c476f76e994a78a6bc830.png) , получим:
, получим:




Таким образом, 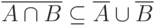 .
.
Аналогично доказывается включение в обратную сторону:
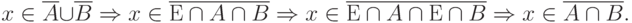
Следовательно,