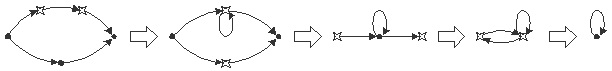| Какие законы позволяют построить аппарат математически эквивалентных преобразований символьно-числовых выражений |
Развертки и граф-машина
Как уже отмечалось ранее, при заданном алгоритме и входных данных граф алгоритма определяется однозначно и представляет информационное ядро алгоритма. Такая его интерпретация связана с тем, что этот граф явно показывает, какая операция алгоритма с какой связана информационно. Всестороннее изучение информационных отношений в процессах реализации алгоритмов или, другими словами, информационной структуры алгоритмов является исключительно важной задачей. В частности, одной из важнейших информационных задач является нахождение всех возможных реализаций алгоритма на вычислительных системах параллельной архитектуры. Ранее было показано, что она эквивалентна описанию всех параллельных форм графа алгоритма. Напомним, что каждая параллельная форма позволяет разбить операции алгоритма на группы. При этом группы операций можно выполнять одна за другой последовательно, а все операции внутри каждой группы - параллельно.
Пока нет никаких оснований, мешающих рассматривать граф алгоритма
как произвольный ориентированный ациклический граф. Без ограничения
общности можно считать, что он размещен в некотором арифметическом
пространстве X подходящей размерности n. Рассмотрим вещественный
функционал  , определенный на точках-вершинах x графа алгоритма G.
Предположим, что дуга идет из точки u в точку v. Будем говорить, что
функционал
, определенный на точках-вершинах x графа алгоритма G.
Предположим, что дуга идет из точки u в точку v. Будем говорить, что
функционал  возрастает (не убывает) вдоль этой дуги, если
возрастает (не убывает) вдоль этой дуги, если 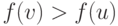 . Назовем функционал
. Назовем функционал  строгой (обобщенной)
разверткой графа G, если он строго возрастает (не убывает) вдоль всех
дуг графа.
строгой (обобщенной)
разверткой графа G, если он строго возрастает (не убывает) вдоль всех
дуг графа.
Степень важности разверток для исследования структуры алгоритмов
через их графы определяется свойствами разверток. Пусть известна
какая-нибудь строгая развертка  . Каждая вершина графа находится на
одной и только на одной поверхности уровня
. Каждая вершина графа находится на
одной и только на одной поверхности уровня 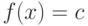 развертки
развертки  .
Разобьем все вершины графа на группы по принадлежности поверхностям
уровней и перенумеруем группы в порядке роста константы c. Ясно, что
группы операций можно выполнять последовательно в том же порядке. На
любой поверхности уровня никакие точки-вершины не могут быть связаны
ни дугами графа алгоритма, ни его путями. Это означает, что
соответствующие таким вершинам операции можно выполнять параллельно.
Другими словами, знание любой строгой развертки позволяет через ее
поверхности уровней построить параллельную форму графа или, что то же
самое, параллельную форму алгоритма. Верно и обратное: любой
параллельной форме можно сопоставить вполне определенную строгую
развертку. Для ее построения необходимо положить значение развертки в
каждой вершине x равным номеру того яруса параллельной формы, в
котором располагается эта вершина x.
.
Разобьем все вершины графа на группы по принадлежности поверхностям
уровней и перенумеруем группы в порядке роста константы c. Ясно, что
группы операций можно выполнять последовательно в том же порядке. На
любой поверхности уровня никакие точки-вершины не могут быть связаны
ни дугами графа алгоритма, ни его путями. Это означает, что
соответствующие таким вершинам операции можно выполнять параллельно.
Другими словами, знание любой строгой развертки позволяет через ее
поверхности уровней построить параллельную форму графа или, что то же
самое, параллельную форму алгоритма. Верно и обратное: любой
параллельной форме можно сопоставить вполне определенную строгую
развертку. Для ее построения необходимо положить значение развертки в
каждой вершине x равным номеру того яруса параллельной формы, в
котором располагается эта вершина x.
Таким образом, между строгими развертками и параллельными формами алгоритма установлено взаимное соответствие. Граф алгоритма и развертки являются математическими объектами. Следовательно, на основе их использования можно создать математический аппарат для изучения параллелизма в алгоритмах. Эффективность изучения во многом будет зависеть от того, насколько в подходящем для исследований виде удастся представить граф алгоритма и в каком классе функционалов придется искать развертки. Вполне возможно, что в желаемом классе не окажется ни одной строгой развертки. И тогда окажутся важными обобщенные развертки, по крайней мере, как естественное замыкание множества строгих разверток.
Прежде чем переходить к математическим исследованиям, полезно рассмотреть компьютерную интерпретацию графа алгоритма и его разверток. Она поможет в дальнейшем лучшему пониманию получаемых результатов. Перенумеруем каким-либо образом все вершины графа. Развертки определены на конечном числе точек. Поэтому строгую или обобщенную развертку можно также задать вектором, в котором размерность равна числу вершин графа алгоритма, номер координаты совпадает с номером вершины, а значение каждой координаты есть значение развертки в соответствующей точке. Рассмотрим какую-нибудь реализацию какой-нибудь схемы алгоритма на каком-нибудь реальном параллельном или последовательном компьютере. Каковы бы не были архитектура компьютера, времена выполнения операций и времена передачи данных, реализация алгоритма однозначно определяет временные моменты окончания всех его операций. Сохранив соответствие между номерами координат и номерами вершин графа алгоритма, составим из этих моментов вектор. Очевидно, что он представляет строгую развертку. Следовательно, множество строгих разверток графа алгоритма содержит в качестве своего подмножества все реальные реализации самого алгоритма.
Поместим в каждую вершину графа алгоритма функциональное устройство, имеющее возможность выполнять соответствующую операцию. Пусть дуги графа представляют линии связи, обеспечивающие передачу информации от одного устройства к другому. Будем теперь рассматривать эту конструкцию как абстрактную специализированную вычислительную систему. Предположим, что после запуска системы все ее функциональные устройства начинают работать под собственным управлением, соблюдая следующие простые правила. Именно, входные данные по мере необходимости доступны потребляющим их устройствам без каких-либо задержек; кроме неотрицательности не накладываются никакие ограничения на времена выполнения операций и времена передачи данных по линиям связи; каждое функциональное устройство может начинать выполнение операции в любой момент после того, как будут готовы для использования все ее аргументы. Назовем построенную систему граф-машиной и будем считать, что режимы ее функционирования описываются множеством разверток графа алгоритма.
Выше отмечалось, что среди этих режимов заведомо присутствуют такие, которые отражают любые реальные реализации алгоритма. Но очевидно, что имеются и другие режимы функционирования граф-машины, которые следует отнести к каким-то гипотетическим реализациям на гипотетических компьютерах. Возможно, наличие именно этих режимов позволит находить более эффективные схемы реализации конкретных алгоритмов и, следовательно, разрабатывать для них вычислительные системы более подходящей архитектуры.
Конечно, не стоит рассматривать граф-машину как прямой прообраз некоторой реальной вычислительной системы. В этом отношении она имеет немало недостатков. В ней очень много функциональных устройств и линий связи, каждое устройство и каждая линия связи срабатывают только по одному разу, совсем не используется память и т.д. Более того, несмотря на большое число устройств, граф-машина имеет возможность реализовывать только один алгоритм. Однако граф-машина и не предназначена для того, чтобы быть непосредственным прообразом реальной универсальной системы. Имеются две основные области ее использования. Во-первых, граф-машина является хорошим инструментом для изучения любых существующих и даже еще не существующих реализаций конкретного алгоритма. И, во-вторых, с помощью некоторых специальных преобразований именно из граф-машины можно построить математические модели многих типов вычислительных систем. Среди них имеются и такие, которые реализуют алгоритм за минимально возможное время, но обладают лучшими "техническими" характеристиками.
Несколько слов об этих преобразованиях. В их основе лежит
гомоморфная свертка граф-машины в граф некоторой вычислительной
системы со многими функциональными устройствами. Рассмотрим
произвольный ориентированный граф  с множеством вершин
с множеством вершин  и множеством
дуг
и множеством
дуг  . Сейчас граф может не быть ациклическим и может содержать петли.
Выберем в
. Сейчас граф может не быть ациклическим и может содержать петли.
Выберем в  любые две вершины
любые две вершины 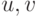 и сольем их в одну вершину
и сольем их в одну вершину  . Новое
множество вершин обозначим
. Новое
множество вершин обозначим 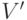 . Перенесем на
. Перенесем на 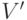 без изменения те дуги из
без изменения те дуги из  , для которых концевые вершины не совпадают ни с u, ни с v. Если же
какая-то из концевых вершин совпадает с
, для которых концевые вершины не совпадают ни с u, ни с v. Если же
какая-то из концевых вершин совпадает с  или
или  , то такие дуги
перенесем с заменой этих вершин на
, то такие дуги
перенесем с заменой этих вершин на  . И, наконец, в новом графе все
петли, относящиеся к одной вершине, заменим одной петлей. Также
заменим одной дугой все кратные дуги одной ориентации. Множество дуг
на
. И, наконец, в новом графе все
петли, относящиеся к одной вершине, заменим одной петлей. Также
заменим одной дугой все кратные дуги одной ориентации. Множество дуг
на 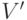 обозначим
обозначим  . Граф с множеством вершин
. Граф с множеством вершин 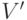 и множеством дуг
и множеством дуг  обозначим
обозначим 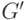 . Преобразование графа
. Преобразование графа  в граф
в граф 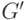 называется простым
гомоморфизмом, а многократное преобразование простого гомоморфизма
называется гомоморфной сверткой графа. При гомоморфной свертке графа G
множество его вершин распадается на непересекающиеся подмножества.
Каждое из подмножеств состоит из тех и только тех вершин, которые в
конечном счете сливаются в одну вершину. Ясно, что любой
ориентированный граф всегда можно гомоморфно свернуть в граф,
состоящий из одной вершины и одной петли. Пример операций простого
гомоморфизма приведен на рис. 7.1. Сливаемые вершины обозначены на нем
"звездочками".
называется простым
гомоморфизмом, а многократное преобразование простого гомоморфизма
называется гомоморфной сверткой графа. При гомоморфной свертке графа G
множество его вершин распадается на непересекающиеся подмножества.
Каждое из подмножеств состоит из тех и только тех вершин, которые в
конечном счете сливаются в одну вершину. Ясно, что любой
ориентированный граф всегда можно гомоморфно свернуть в граф,
состоящий из одной вершины и одной петли. Пример операций простого
гомоморфизма приведен на рис. 7.1. Сливаемые вершины обозначены на нем
"звездочками".
Простым и конструктивным приемом осуществления гомоморфной свертки
является операция проектирования. Если граф расположен в пространстве  , то спроектируем его вдоль любой прямой на перпендикулярную
гиперплоскость. Пусть при этом какие-то вершины спроектируются в одну
точку. Если в ту же точку спроектируются некоторые вектор-дуги, то
поставим около точки петлю. Очевидно, что подобная операция есть
гомоморфная свертка графа
, то спроектируем его вдоль любой прямой на перпендикулярную
гиперплоскость. Пусть при этом какие-то вершины спроектируются в одну
точку. Если в ту же точку спроектируются некоторые вектор-дуги, то
поставим около точки петлю. Очевидно, что подобная операция есть
гомоморфная свертка графа  . Чем больше точек-вершин графа расположено
по направлению проектирования, тем больше вершин спроектируются в одну
точку. Ничто не мешает повторять операцию проектирования многократно,
пока не получится граф нужного строения. После числа шагов, равного
размерности пространства, всегда в проекции получится одна точка. Если
в графе
. Чем больше точек-вершин графа расположено
по направлению проектирования, тем больше вершин спроектируются в одну
точку. Ничто не мешает повторять операцию проектирования многократно,
пока не получится граф нужного строения. После числа шагов, равного
размерности пространства, всегда в проекции получится одна точка. Если
в графе  была хотя бы одна дуга, то около точки будет петля.
была хотя бы одна дуга, то около точки будет петля.
Гомоморфная свертка имеет очень прозрачный "компьютерный"
смысл. Если граф  представляет граф-машину, то, выбирая вершины
представляет граф-машину, то, выбирая вершины 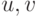 ,
мы определяем две операции алгоритма и два ФУ, которые эти операции
реализуют. Сливая вершины
,
мы определяем две операции алгоритма и два ФУ, которые эти операции
реализуют. Сливая вершины 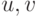 , мы связываем с вершиной
, мы связываем с вершиной  не одну, а
пару операций. ФУ, соотответствующее вершине
не одну, а
пару операций. ФУ, соотответствующее вершине  , должно иметь
возможность выполнить обе операции последовательно. После
многократного применения операции простого гомоморфизма полученный
граф можно рассматривать как граф новой модели вычислительной системы.
ФУ, связанное с любой его вершиной, обязано последовательно выполнять
все операции алгоритма, связанные со всеми вершинами-прообразами. Дуги
по-прежнему символизируют направленные передачи информации. Наличие
петли около вершины говорит о том, что соответствующее ФУ будет
срабатывать многократно.
, должно иметь
возможность выполнить обе операции последовательно. После
многократного применения операции простого гомоморфизма полученный
граф можно рассматривать как граф новой модели вычислительной системы.
ФУ, связанное с любой его вершиной, обязано последовательно выполнять
все операции алгоритма, связанные со всеми вершинами-прообразами. Дуги
по-прежнему символизируют направленные передачи информации. Наличие
петли около вершины говорит о том, что соответствующее ФУ будет
срабатывать многократно.
Имеется одно принципиальное отличие граф-машины от вычислительной системы, полученной при гомоморфной свертке. Граф-машина не имеет память. Роль ее ячеек успешно выполняют сами ФУ в силу того, что каждое из них срабатывает только один раз. При многократном срабатывании ФУ для сохранения результатов предшествующих срабатываний уже нужна память. Зная граф алгоритма и временной режим срабатываний ФУ новой системы, можно подсчитать величину требуемой памяти и даже изучить процесс ее использования.
В общем случае на вычислительной системе, полученной после гомоморфной свертки, нельзя реализовать все временные режимы, допустимые для граф-машины. Тем не менее, имеет место важная
Теорема о гомоморфной свертке. Пусть при гомоморфной свертке граф- машины сливаются лишь вершины, связанные едиными путями. Тогда на вычислительной системе с полученным графом можно реализовать то же множество временных режимов, что и на граф-машине.
Достаточная разнесенность во времени моментов включения ФУ построенной системы гарантируется здесь тем, что сливаемые вершины находятся на одном пути. Поэтому соответствующие им операции как обязаны были раньше, так и имеют возможность теперь выполняться последовательно друг за другом. Подчеркнем также, что совсем не обязательно, чтобы образ сливаемых вершин имел в качестве своих прообразов все вершины, находящиеся на одном пути. Важно лишь, чтобы прообразы были связаны одним путем. Это обстоятельство имеет существенное значение, так как чаще всего объединяются вершины, соответствующие однотипным операциям, а они обычно в вычислениях перемешиваются с операциями других типов. Что же касается установления соответствия между вершинами графа алгоритма и срабатываниями ФУ, помещенными в вершины графа вычислительной системы, полученной после гомоморфной свертки, то теперь оно очень простое. Именно, если из двух вершин графа алгоритма одна достижима из другой, то из двух соответствующих срабатываний ФУ ей соответствует более позднее.
Таким образом, разбивая вершины графа алгоритма на подмножества, лежащие на одном пути, и объединяя их с помощью операций простого гомоморфизма, мы получаем конструктивный способ построения математических моделей вычислительных систем. Естественно, что таких систем может быть много, и о ни, вообще говоря, не одинаковы с точки зрения состава ФУ, их загруженности, размера присоединенной памяти, сложности коммуникационной сети и т. п. Но все эти системы по своим основным параметрам, кроме размера памяти, лучше, чем граф-машина. Они содержат меньшее число ФУ, загруженность каждого ФУ больше, число линий связи между ФУ меньше и при этом часто реализуется весь спектр временных режимов, включая наискорейшие. Снова можно ставить задачу оптимизации, пытаясь разбить вершины графа алгоритма на наименьшее число подмножеств, лежащих на одном пути. И снова возникает противоречивая ситуация: уменьшение числа ФУ может привести к усложнению коммуникационной сети и увеличению объема памяти. Описанная свертка граф-машины была с успехом использована при построении математических моделей систолических массивов [ 1 ] .