| Какие объекты исследует вычислительная математика |
Численное решение переопределенных СЛАУ. Метод наименьших квадратов
Теорема. Пусть столбцы матрицы  линейно
независимы, т.е. ранг
линейно
независимы, т.е. ранг  равен p. Тогда существует единственный элемент p - мерного евклидова пространства
равен p. Тогда существует единственный элемент p - мерного евклидова пространства 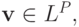 являющийся обобщенным решением системы (3.2), и решением СЛАУ
являющийся обобщенным решением системы (3.2), и решением СЛАУ
 |
( 3.5) |
состоящей из p скалярных уравнений относительно неизвестных  доставляющий минимум квадратичной форме
доставляющий минимум квадратичной форме
![\Phi (\mathbf{u}) = {\left[\mathbf{Au} - \mathbf{f}, \mathbf{Au} - \mathbf{f}\right]}^n.](/sites/default/files/tex_cache/048d2f7a9b582c83013362ad78a80d7c.png)
Доказательство.
Покажем, что решение СЛАУ 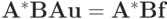 существует и единственно. Введем обозначение
существует и единственно. Введем обозначение  для вектора — k столбца матрицы системы
для вектора — k столбца матрицы системы  :
:
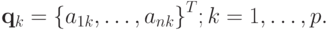
Несложно показать, что матрица  системы (3.5) есть квадратная матрица p x p. Элемент dij этой матрицы, стоящий на пересечении i строки и j столбца, есть
системы (3.5) есть квадратная матрица p x p. Элемент dij этой матрицы, стоящий на пересечении i строки и j столбца, есть ![d_{ij} = {({\mathbf{q}}_i, {\mathbf{Bq}}_j)}^n = {({\mathbf{Bq}}_i,{\mathbf{q}}_j)}^n = {\left[{{\mathbf{q}}_i,{\mathbf{q}}_j}\right]}^n,](/sites/default/files/tex_cache/1566b9d4f1fb60245e6bff672ba84a3b.png) в силу коммутативности скалярного произведения dij = dij, что означает самосопряженность матрицы
в силу коммутативности скалярного произведения dij = dij, что означает самосопряженность матрицы 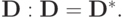
Покажем, что матрица 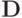 невырождена и положительно
определена. Напомним, что
невырождена и положительно
определена. Напомним, что 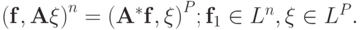 Это равенство проверяется непосредственно, если записать обе его части в
развернутом виде. Невырожденность матрицы
Это равенство проверяется непосредственно, если записать обе его части в
развернутом виде. Невырожденность матрицы 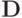 следует из того, что ранг матрицы
следует из того, что ранг матрицы  равен p.
равен p.
В таком случае ![0 < {\left[{\mathbf{Ax},\mathbf{x}}\right]}^n =
{(\mathbf{BAx},\mathbf{Ax})}^n = {({\mathbf{A}}^*{\mathbf{BAx}},{\mathbf{x}})}^p = {(\mathbf{Dx},\mathbf{x})}^p.](/sites/default/files/tex_cache/0108a40ec5cda662149065b9f880e44a.png) Поскольку
Поскольку 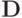 невырождена и положительно определена, то (3.5) имеет единственное решение
невырождена и положительно определена, то (3.5) имеет единственное решение 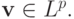 Теперь покажем, что
Теперь покажем, что  — единственное
обобщенное решение системы. Для любого вектора
— единственное
обобщенное решение системы. Для любого вектора  выполнено
выполнено 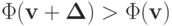 :
:
![\Phi (\mathbf{v} + \mathbf{\Delta }) = {\left[{\mathbf{A}(\mathbf{v} +
\mathbf{\Delta }) - \mathbf{f},\mathbf{A}(\mathbf{v} + \mathbf{\Delta }) - \mathbf{f}}\right]}^n = \\
= {\left[{\mathbf{Av} - \mathbf{f},\mathbf{Av} - \mathbf{f}}\right]}^n -
2{\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n +
{\left[{\mathbf{A\Delta },\mathbf{A\Delta }}\right]}^n = \\
= \Phi (\mathbf{v}) + {2\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n + {(\mathbf{D\Delta },\mathbf{\Delta })}^p = \Phi (\mathbf{v}) + {(\mathbf{D\Delta },\mathbf{\Delta })}^p > \Phi (\mathbf{v}),](/sites/default/files/tex_cache/48f94b1d9f83ae71683436e2795d8ba3.png)
что и требовалось доказать.
При доказательстве использовалось
![{\left[{\mathbf{Av} - \mathbf{f},\mathbf{A\Delta }}\right]}^n =
{(\mathbf{B}(\mathbf{Av} - \mathbf{f}),\mathbf{A\Delta })}^n =
{({\mathbf{A}}^*{\mathbf{BAv}} - {\mathbf{A}}^*{\mathbf{Bf}},\mathbf{\Delta
})}^p = 0,](/sites/default/files/tex_cache/56ebfd5acd49ab2a201c1ec66bb08c0a.png)
поскольку 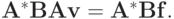
Так как матрица  — симметричная и положительно определенная, то для численного решения полученной СЛАУ можно воспользоваться итерационными методами.
— симметричная и положительно определенная, то для численного решения полученной СЛАУ можно воспользоваться итерационными методами.
Если система векторов 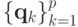 оказывается ортонормированной, т.е.
оказывается ортонормированной, т.е. ![[{\mathbf{q}}_i,{\mathbf{q}}_j ] = \delta_{ij} i,j = 1, \ldots, p,](/sites/default/files/tex_cache/d072e48afb16d243e80a6fc36cc6244e.png) то матрица
то матрица 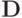 оказывается единичной. Ее
элементы и есть скалярные произведения
оказывается единичной. Ее
элементы и есть скалярные произведения ![[{\mathbf{q}}_i,{\mathbf{q}}_j ].](/sites/default/files/tex_cache/5ba004985bea375511f025253d4e4a94.png) В этом случае решением системы будет
В этом случае решением системы будет

Следует отметить, что если базисные функции 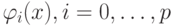 не выбираются специальным образом, то при достаточно больших p
не выбираются специальным образом, то при достаточно больших p 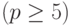 полученная СЛАУ оказывается плохо обусловленной. Строки матрицы
полученная СЛАУ оказывается плохо обусловленной. Строки матрицы  могут оказаться почти линейно зависимыми. Простейшим примером такого почти линейно зависимого базиса является система функций xi, i = 1, ..., p при больших p. В этом случае желательно использовать ортогональные функциональные базисы, однако такой выбор не
всегда возможен и удобен.
могут оказаться почти линейно зависимыми. Простейшим примером такого почти линейно зависимого базиса является система функций xi, i = 1, ..., p при больших p. В этом случае желательно использовать ортогональные функциональные базисы, однако такой выбор не
всегда возможен и удобен.
Для примера возьмем в качестве базисных функций степенные, обобщенный полином в этом случае будет
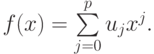
Скалярные произведения на отрезке [0, 1], записанные в интегральной форме (т.е. при 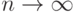 ), будут иметь вид
), будут иметь вид
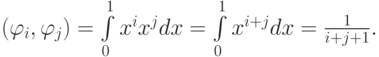
В таком случае СЛАУ после применения МНК, т.е. минимизации функционала 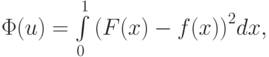 где F(x) — заданная функция, будет:
где F(x) — заданная функция, будет:
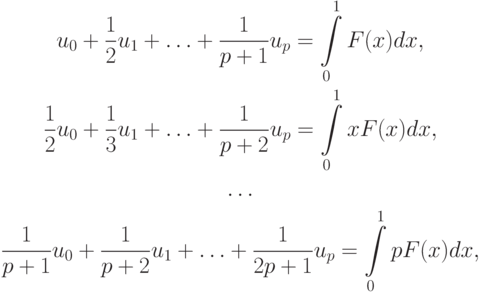
или
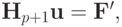
где
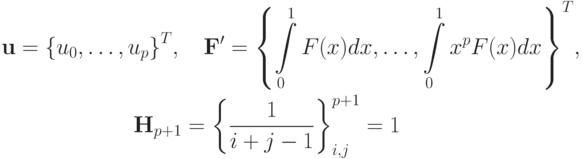
Матрица 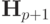 называется матрицей Гильберта. Это
классический пример плохо обусловленной матрицы. Число обусловленности очень быстро растет с ростом p. Так при p = 1
называется матрицей Гильберта. Это
классический пример плохо обусловленной матрицы. Число обусловленности очень быстро растет с ростом p. Так при p = 1  при
при 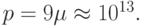 Если получим СЛАУ для дискретной системы точек, т.е. для
Если получим СЛАУ для дискретной системы точек, т.е. для
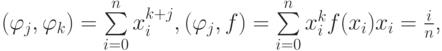
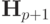 при
при