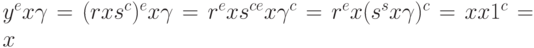НОУ ИНТУИТ | Управление ключами шифрования и безопасность сети. Лекция 4: Установление подлинности объекта

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 19.01.2010 | Уровень: специалист | Доступ: свободно

|

Вам нравится? Нравится 20 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

4.4. Подтверждение с нулевым разглашением

При установлении подлинности пароля претендент должен передать свой секрет ( пароль ) верификатору; это может привести к перехвату информации Евой. Кроме того, нечестный верификатор может показать пароль другим или использовать его, чтобы исполнить роль претендент а.

При установлении подлинности объекта методом вызова-ответа секрет претендент а не передают верификатору. Претендент применяет некоторую функцию для обработки вызова, которая передана верификатором, но при этом включает свой секрет. В некоторых методах "вызова-ответа" верификатор фактически знает секрет претендент а, при этом он может неправильно использоваться нечестной верификацие й. В других методах верификатор может извлечь некоторую информацию о секрете претендент а, выбирая заранее запланированное множество вызовов.

В установлении подлинности с нулевым разглашением претендент не раскрывает ничего, что могло бы создать угрозу конфиденциальности секрета. Претендент доказывает верификатору, что он знает секрет, не раскрывая и не показывая его. В таком случае взаимодействие разработано так, чтобы не привести к раскрытию или предположению о содержании секрета. После обмена сообщениями верификатор только знает, что претендент имеет или не имеет секрета - и ничего больше. В этой ситуации результат - да/нет. Это единственный бит информации.

В установлении подлинности с нулевым разглашением претендент доказывает, что он знает секрет, не показывая его.

Протокол Фиата-Шамира

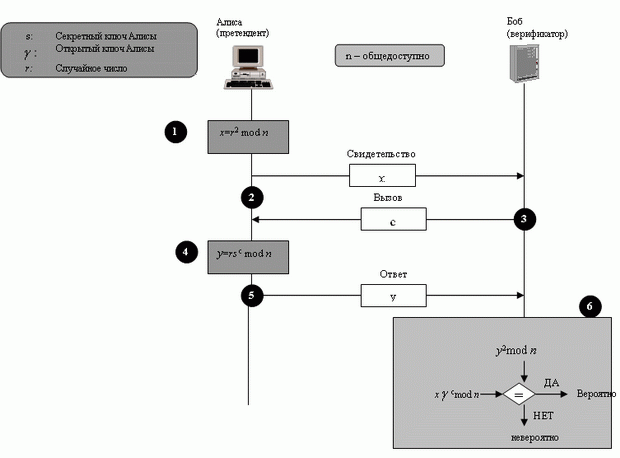
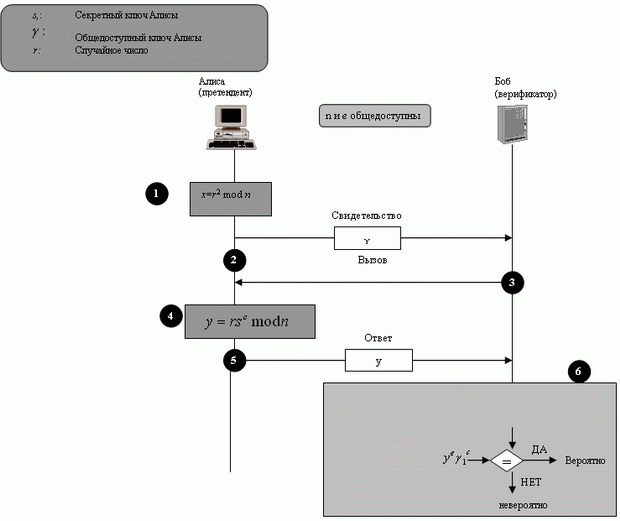
В протоколе Фиата-Шамира (Amos Fiat, Adi Shamir) третье лицо, которому доверяют (см. "Управление ключами" ), выбирает два больших простых числа p и q, чтобы вычислить значение n = p x q. Значение n объявляется общедоступным. Значения p и q сохраняются секретными. Алиса, претендент, выбирает секретное число s между 1 и n - 1. Она вычисляет v = s² mod n. Она сохраняет s как свой секретный ключ и регистрирует v как свой общедоступный ключ вместе с третьим лицом. Проверка Алисы Бобом может быть сделана в четыре шага, как показано на рис. 4.13.

Алиса- претендент выбирает случайное число r между 0, и n - 1 ( r называется "обязательство"). Она затем вычисляет значение
x = r²mod n ( x называется "свидетельство").
Алиса передает x Бобу как свидетельство.
Боб-верификатор передает вызов c Алисе. Значение c равно или 0, или 1.
Алиса вычисляет свой ответ y = rs^c. Обратите внимание, что r - случайное число, выбранное Алисой на первом шаге, s - ее секретный ключ и c - признак ( 0 или 1 ).
Алиса передает ответ Бобу, чтобы показать, что она знает значение своего секретного ключа, s. Она подтверждает, что это была именно Алиса.
Боб вычисляет y² и x^c. Если эти два значения являются конгруэнтными, то для Алисы значение s означает "она честна"; или она вычислила значение y другим способом ("она нечестная"), потому что мы можем легко доказать, что y - тот же самый, как x^c по модулю n:
```
y²= (rs^c)²= r²s^2c = r²(s²)^c= x^c
```

увеличить изображение
Рис. 4.13. Протокол Фиата - Шамира

Раунд состоит из шести шагов; верификация повторяется несколько раз со значением c, равным 0 или 1 (выбираются случайно). В каждом раунде, который будет верифицирован, претендент должен передать результат испытания. Если не проходит хотя бы один раунд, процесс прерывается и формируется сообщение, что Алиса не прошла испытание на подлинность.

Давайте рассмотрим этот тщательно продуманный и интересный протокол. Алиса может быть честна (знает значение s ) или нечестна (не знает значение s ). Если она честна, она проходит каждый раунд. Если нет - она может пройти раунд, правильно предсказывая значение вызова. При этом могут возникнуть две ситуации:

Алиса предполагает, что значение c (выход) будет 1 (предсказание). Она вычисляет 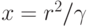и передает x как свидетельство.
- Если ее предположение правильно (оказалось, что c был равен 1), она передает y = r как ответ. Мы можем видеть, что она передаст результат, который соответствует тесту $(y^{2} = x^{\gamma с})$ .
- Если ее предположение неправильно (оказалось, что c, было 0), она не может найти значение y, которое соответствует тесту. Она, вероятно, выходит из игры или передаст значение, которое не соответствует ожидаемому результату теста, и Боб прервет процесс.
Алиса предполагает, что значение c (вызов) будет 0. Она вычисляет x = r и передает x как свидетельство.
- Если ее предположение правильно (оказалось, что c было 0), она передает y = r как ответ. Она передает результат испытания, который соответствует $(y^{2} = x^{\gamma с})$ .
- Если ее предположение неправильно (оказалось, что c было 1), она не может найти значение y, которое соответствует тесту. Она, вероятно, выходит из игры или передаст значение, которое не соответствует ожидаемому результату теста, и Боб прервет процесс.

Мы можем видеть, что нечестный претендент имеет 50-процентный шанс на введение в заблуждение верификатора, проводящего испытание (предсказывая значение вызова). Другими словами, Боб назначает вероятность 1/2 для каждого раунда испытания. Если процесс повторяется 20 раз, вероятность уменьшается до (1/2)²⁰ или 9,54 x 10^-7. Другими словами, просто невероятно, что Алиса может правильно предсказать 20 раз.

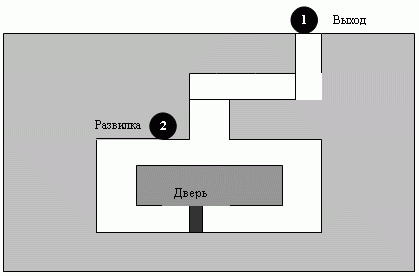
Пример "пещера Аладдина". Чтобы показать логику вышеупомянутого протокола, Жан-Жак Кискатер (Quisquater) и Гиом Гийу (Gillou) изобрели пример "пещера Аладдина" ( рис. 4.14).

Рис. 4.14. Одноразовый пароль Лампорта

Предположим, что есть подземная пещера с дверью в конце, которая может быть открыта только с помощью волшебного слова. Алиса утверждает, что она знает это слово и что она может открыть дверь. Вначале Алиса и Боб стоят у входа (точка 1). Алиса входит в пещеру и достигает разветвления (точка 2). Боб, стоя у входа, не может видеть Алису. Теперь начинается игра.

Алиса выбирает, куда идти: или направо, или налево. И говорит об этом Бобу (соответствует передаче свидетельства x ).
После того как Алиса исчезает в пещере, Боб подходит к разветвлению (точка 2) и просит, чтобы Алиса вышла или справа, или слева. Это соответствует передаче вызова ( c ).
Если Алиса знает волшебное слово (свой секретный ключ), она может выйти с запрошенной стороны. Ей, вероятно, придется использовать волшебное слово (если она находится на неправильной стороне), или она может выйти, не используя волшебное слово (если она - на правильной стороне). Однако если Алиса не знает волшебное слово, она может выйти только с правильной стороны, если она разгадала вызов Боба. С вероятностью 1/2 Алиса может убедить глупого Боба, что она знает волшебное слово. Это соответствует ответу ( y ).
Игра повторяется много раз. Алиса победит, если она все время проходит испытания положительно. Вероятность, что она победит в игре, если она не знает волшебное слово, очень низка. Другими словами, P = (1/2)^N, где P - вероятность победы, если она не знает волшебное слово.
N - количество раз повторения испытания.

Протокол Фейге-Фиата-Шамира

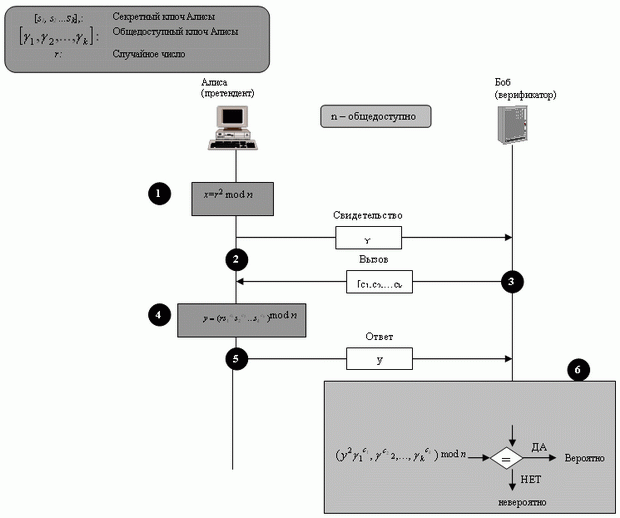
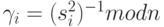Протокол Фейге-Фиата-Шамира (Feige-Fiat-Shamir) подобен первому подходу за исключением того, что он использует вектор секретных ключей [s₁, s₂ ...s_k], вектор общедоступных ключей $[\gamma _{1}, \gamma _{2} \dots \gamma _{k}]$ и векторы признаков ( c₁,c₂,...,c_k). Секретные ключи выбраны случайно, но они должны быть взаимно простыми с n. Общедоступные ключи выбраны так, что $\gamma _{i} = (s_{i}^{2})^{-1} mod n$ . На рис. 4.15 показаны три шага в процессе.

увеличить изображение
Рис. 4.15. Протокол Фейге - Фиата - Шамира

Мы можем доказать, что $y^{2} \gamma ^{c1}_{1}, \gamma ^{c2}_{2}, \dots , \gamma ^{ck}_{k}$ имеет то же значение, что и x:

$y^{2} \gamma _{1}^{c1}, \gamma _{2}^{c2}, \dots , \gamma _{k}^{ck} = r^{2}(s_{1}^{c1})^{2}(s_{2}^{c2})^{2}\dots (s_{k}^{ck})^{2}\gamma _{1}^{c1}, \gamma _{2}^{c2}, \dots , \gamma _{k}^{ck} = x(s_{1}^{2})^{c1}(\gamma _{1}^{c1})(s_{2}^{2})^{c2}(\gamma _{2}^{c2})\dots (s_{k}^{2})^{ck}(\gamma _{k}^{ck}) = x(s_{1}^{2} \gamma _{1}^{c1})^{c1}(s_{2}^{2}\gamma _{2}^{c2})^{c2}\dots (s_{k}^{2}\gamma _{k}^{ck})^{ck} = x(1)^{c1}(1)^{c2} \dots (1)^{ck} = x$

Три шага составляют раунд; проверка повторяется несколько раз со значением индекса s, равным 0 или 1 (выбирается случайно). Претендент должен провести испытание в каждом раунде, который проверяется. Если претендент ошибается в одном раунде, процесс прерывается и подлинность не подтверждается.

Протокол Кискатера-Гийу

Протокол Кискатера (Quisquater) и Гийу (Gillou) расширяет протокол Фиата-Шамира, в котором может быть использовано меньшее число раундов, чтобы доказать полномочность претендент а. Третье лицо, которому доверяют (см. "Управление ключами" ), выбирает два больших простых числа p и q, чтобы вычислить значение n = p x q.

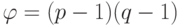Сторона, которой доверяют, также выбирает показатель $\phi,$ e, который является взаимно-простым с , где $\varphi = (p - 1) (q - 1)$ . Значения n и e объявляются общедоступными; значения p и q сохраняются секретными. Сторона, которой доверяют, выбирает два числа для каждого объекта: число , которое является общедоступным, и число s, которое является секретным. Однако в этом случае отношения между $\gamma$ и s определяются уравнением

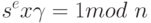
$s^{e} x \gamma = 1 mod \ n$

Три шага составляют раунд; проверка повторяется несколько раз со случайным значением c (вызов - challenge) между 1 и e. Претендент должен передать результат испытания в каждом раунде, который будет проверяться. Если претендент передал неверно хотя бы один раунд, процесс прерывается и сообщение признается неподлинным. рис. 4.16 иллюстрирует один раунд.

увеличить изображение
Рис. 4.16. Протокол Кискатера - Гию

Равенство может быть доказано так, как показано ниже:

$y^{e} x \gamma = ( r x s^{c})^{e} x \gamma = r^{e} x s^{ce} x \gamma ^{c} = r^{e} x (s^{s} x \gamma )^{c} = x x 1^{c} = x$

Дальше >>

Управление ключами шифрования и безопасность сети

Установление подлинности объекта