| Как сбросить прогресс по курсу? Хочу начать заново |
Введение в наследование
Ранее изученные приемы явно недостаточны. Классы, конечно, дают способ хорошей декомпозиции на модули и обладают многими качествами, ожидаемыми от повторно используемых компонентов: они являются однородными, согласованными модулями; в соответствии с принципом Скрытия информации можно легко отделять интерфейсы от реализаций; универсальность придает им определенную гибкость, а благодаря утверждениям, можно точно задавать их семантику. Но для достижения повторного использования и расширяемости нужно нечто большее.
Всякий комплексный подход, обеспечивающий повторное использование, должен столкнуться с проблемой повторяемости (repetition) и изменчивости (variation), проанализированной в одной из предыдущих лекций (см. "Подходы к повторному использованию" ). Для устранения многократного переписывания одного и того же кода, ведущего к потерям времени, появлению противоречий и ошибок, нужны методы, улавливающие поразительную общность, присущую многим группам однотипных структур - всем текстовым редакторам, всем таблицам, всем программам обработки файлов, - учитывая при этом многие различия в характеристиках конкретных случаев.
При обеспечении расширяемости (extendibility) преимущество описанной выше системы типов состоит в гарантированной совместности во время компиляции, но она запрещает многие вполне законные комбинации элементов. Например, нельзя объявить массив, содержащий геометрические объекты различных совместных типов, таких как POINT (ТОЧКА) и SEGMENT(ОТРЕЗОК).
Чтобы достичь прогресса в повторном использовании или в расширяемости требуется воспользоваться преимуществами концептуальных отношений между классами: один класс может быть расширением, специализацией или комбинацией других классов. Метод и язык должны поддерживать запись и использование этих отношений. Эту поддержку выполняет наследование.
Центральная и восхитительная составляющая объектной технологии - отношение наследования - потребует для полного освоения нескольких лекций. В данной лекции рассматриваются фундаментальные понятия. В трех следующих описываются более специальные аспекты: множественное наследование, переименование, субконтракты, влияние на систему типов. Лекция 6 курса "Основы объектно-ориентированного проектирования" дополнит эти технические рассмотрения, рассмотрев методологическую перспективу: как использовать наследование и как избежать его неверного применения.
Многоугольники и прямоугольники
Для объяснения основных понятий рассмотрим простой пример. Здесь приведен скорее набросок этого примера, а не полный его вариант, но он хорошо показывает все существенные идеи.
Многоугольники
Предположим, что требуется построить графическую библиотеку. Ее классы будут описывать геометрические абстракции: точки, отрезки, векторы, круги, эллипсы, многоугольники, треугольники, прямоугольники, квадраты и т. п.
Рассмотрим вначале класс, описывающий многоугольники. Операции будут включать вычисление периметра, параллельный перенос и вращение. Этот класс может выглядеть так:
indexing
description: "Многоугольники с произвольным числом вершин"
class POLYGON creation
...
feature -- Доступ
count: INTEGER
-- Число вершин
perimeter: REAL is
-- Длина периметра
do ... end
feature -- Преобразование
display is
-- Вывод многоугольника на экран.
do ... end
rotate (center: POINT; angle: REAL) is
-- Поворот на угол angle вокруг точки center.
do
... См. далее ...
end
translate (a, b: REAL) is
-- Сдвиг на a по горизонтали, на b по вертикали.
do ... end
... Объявления других компонентов ...
feature {NONE} -- Реализация
vertices: LINKED_LIST [POINT]
-- Список вершин многоугольника
invariant
same_count_as_implementation: count = vertices.count
at_least_three: count >= 3
-- У многоугольника не менее трех вершин (см. упражнение У14.2)
endАтрибут vertices задает список вершин, выбор линейного списка - это лишь одно из возможных представлений (массив мог бы оказаться лучше).
Приведем реализацию типичной процедуры rotate. Эта процедура осуществляет поворот на заданный угол вокруг заданного центра поворота. Для поворота многоугольника достаточно повернуть по очереди каждую его вершину.
rotate (center: POINT; angle: REAL) is
-- Поворот вокруг точки center на угол angle.
do
from
vertices.start
until
vertices.after
loop
vertices.item.rotate (center, angle)
vertices.forth
end
endЧтобы понять эту процедуру заметим, что компонент item из LINKED_LIST возвращает значение текущего элемента списка. Поскольку vertices имеют тип LINKED_LIST [POINT], то vertices.item обозначает точку, к которой можно применить процедуру поворота rotate, определенную для класса POINT в предыдущей лекции. Это вполне корректно и достаточно общепринято - давать одно и то же имя (в данном случае rotate ), компонентам разных классов, поскольку результирующее множество каждого из них имеет свой явно определенный тип. (Это ОО-форма перегрузки.)
Более важна для наших целей процедура вычисления периметра многоугольника. Единственный способ вычислить периметр многоугольника - это в цикле пройти по всем его вершинам и просуммировать длины всех ребер. Вот возможная реализация процедуры perimeter:
perimeter: REAL is
-- Сумма длин ребер
local
this, previous: POINT
do
from
vertices.start; this := vertices.item
check not vertices.after end -- Следствие условия at_least_three
until
vertices.is_last
loop
previous := this
vertices.forth
this := vertices.item
Result := Result + this.distance (previous)
end
Result := Result + this.distance (vertices.first)
endВ этом цикле просто последовательно складываются расстояния между соседними вершинами. Функция distance была определена в классе POINT. Значение Result, возвращаемое этой функцией, при инициализации получает значение 0. Из класса LINKED_LIST используются следующие компоненты: first дает первый элемент списка, start сдвигает курсор, на этот первый элемент, forth передвигает его на следующий, item выдает значение элемента под курсором, is_last определяет, является ли текущий элемент последним, after узнает, что курсор оказался за последним элементом. Как указано в команде check инвариант at_least_three обеспечивает правильное начало и завершение цикла. Он стартует в состоянии not after, в котором элемент vertices.item определен. Допустимо применение forth один или более раз, что, в конце концов, приведет в состояние, удовлетворяющее условию выхода из цикла is_last.
Прямоугольники
Предположим теперь, что нам требуется новый класс, представляющий прямоугольники. Можно было бы начать его проектировать заново. Но прямоугольники это специальный вид многоугольников и у них много общих компонент: их также можно сдвигать, поворачивать и выводить на экран. С другой стороны, у них есть ряд специфических компонентов (например, диагонали), специальные свойства (число вершин равно четырем, а углы являются прямыми) и возможны специальные варианты некоторых операций (вычисление периметра можно устроить проще, чем в приведенном выше алгоритме).
Преимущества такой смеси общих и специфических компонентов можно использовать, определив класс RECTANGLE как наследника (heir) класса POLYGON. При этом все компоненты класса POLYGON, называемого родителем (parent) класса RECTANGLE, по умолчанию будут применимы и к классу-наследнику. Для этого достаточно включить в RECTANGLE предложение наследования (inheritance clause):
class RECTANGLE inherit POLYGON feature ... Компоненты, специфичные для прямоугольников ... end
В предложении feature класса-наследника компоненты родителя не повторяются: они автоматически доступны благодаря предложению о наследовании. В нем будут указаны лишь компоненты, специфичные для наследника. Это могут быть новые компоненты, такие как diagonal, а также переопределяемые наследуемые компоненты.
Вторая возможность полезна для такого компонента, который уже имелся у родителя, но у наследника должен быть описан в другом виде. Рассмотрим периметр perimeter. Для прямоугольников его можно вычислить более эффективно: не нужно вычислять четыре длины сторон, достаточно удвоить сумму длин двух сторон. Наследник, переопределяющий некоторый компонент родителя, должен объявить об этом в предложении наследования, включив предложение redefine:
class RECTANGLE inherit
POLYGON
redefine perimeter end
feature
...
endЭто позволяет включить в предложение feature класса RECTANGLE новую версию компонента perimeter, которая заменит его версию из класса POLYGON. Если не включить объявление redefine, то новое объявление компонента perimeter среди других компонентов класса RECTANGLE приведет к ошибке, поскольку у RECTANGLE уже есть компонент perimeter, унаследованный от POLYGON, т.е. у некоторого компонента окажется два определения.
Класс RECTANGLE выглядит следующим образом:
indexing
description: "Прямоугольники, - специальный случай многоугольников"
class RECTANGLE inherit
POLYGON
redefine perimeter end
creation
make
feature -- Инициализация
make (center: POINT; s1, s2, angle: REAL) is
-- Установить центр прямоугольника в center, длины сторон
-- s1 и s2 и ориентацию angle.
do ... end
feature -- Access
side1, side2: REAL
-- Длины двух сторон
diagonal: REAL
-- Длина диагонали
perimeter: REAL is
-- Сумма длин сторон
-- (Переопределение версии из POLYGON)
do
Result := 2 S (side1 + side2)
end
invariant
four_sides: count = 4
first_side: (vertices.i_th (1)).distance (vertices.i_th (2)) = side1
second_side: (vertices.i_th (2)).distance (vertices.i_th (3)) = side2
third_side: (vertices.i_th (3)).distance (vertices.i_th (4)) = side1
fourth_side: (vertices.i_th (4)).distance (vertices.i_th (1)) = side2
endТак как RECTANGLE является наследником класса POLYGON, то все компоненты родительского класса применимы и к новому классу: vertices, rotate, translate, perimeter (в переопределенном виде) и все остальные. Их не нужно повторять в определении нового класса.
Этот процесс транзитивен: всякий класс, будучи наследником RECTANGLE, например, SQUARE, также обладает всеми компонентами класса POLYGON.
Основные соглашения и терминология
Кроме терминов "наследник" и "родитель" будут полезны следующие термины:
Терминология наследования
Потомок класса C - это любой класс, который наследует C явно или неявно, включая и сам класс C. (Формально, это либо C, либо, по рекурсии, потомок некоторого наследника C ).
Собственный потомок класса C - это потомок, отличный от самого C.
Предок C - это такой класс A, для которого C является потомком. Собственный предок C - это такой класс A, для которого C является собственным потомком.
В литературе также встречаются термины "подкласс" и "суперкласс", но мы не будем их использовать из-за неоднозначности.
Имеется также терминология для компонентов класса: компонент либо является наследуемым (перешедшим от некоторого собственного предка), либо непосредственным (введенным в данном классе).
При графическом представлении структур ОО-ПО, в котором классы изображаются эллипсами, связи по отношению наследования показываются в виде одинарных стрелок. Тем самым они отличаются от связей по отношению "быть клиентом", которые представляются двойными стрелками.
Переопределяемый компонент отмечается ++ (это соглашение принято в Business Object Notation (B.O.N.)).
Стрелка указывает вверх от наследника к родителю. Это соглашение легко запомнить - оно представляет отношение "наследовать от". В литературе встречается и обратное направление таких стрелок. Хотя обычно выбор графического представления является делом вкуса, в данном случае, одно из них явно лучше другого, поскольку одно наводит на мысль о правильном отношении, а другое может привести к путанице. Стрелка - это не просто произвольная пиктограмма, она указывает на одностороннюю связь между своими двумя концами. В данном случае:
- Всякий экземпляр наследника можно рассматривать как экземпляр родителя, а обратное неверно.
- В тексте наследника всегда упоминается его родитель, но не наоборот. Это, на самом деле, является важным свойством ОО-метода, вытекающим из принципа Открыт-Закрыт, согласно которому класс не "знает" списка своих наследников и других собственных потомков.
Хотя у нас нет жесткого правила, определяющего для достаточно сложных систем размещение классов на диаграммах наследования, мы будем, по возможности, помещать класс выше его наследника.
Наследование инварианта
Хотелось бы указать инвариант класса RECTANGLE, который говорил бы, что число сторон прямоугольника равно четырем и что длины сторон последовательно равны side1, side2, side1 и side2.
У класса POLYGON также имеется инвариант, который применим и к его наследнику:
Правило наследования инварианта
Инвариант класса является конъюнкцией утверждений из его раздела invariant и свойств инвариантов его родителей (если таковые имеются).
Поскольку у родителей класса могут быть свои родители, то это правило рекурсивно: в результате полный инвариант класса получается как конъюнкция собственного инварианта и инвариантов классов всех его предков.
Это правило отражает одну из важных характеристик наследования: сказать, что B наследует A - это утверждать, что каждый экземпляр B является также экземпляром A. Вследствие этого всякое выраженное инвариантом ограничение целостности, применимое к экземплярам A, будет также применимо и к экземплярам B.
В нашем примере второе предложение ( at_least_three ) инварианта POLYGON утверждает, что число сторон должно быть не менее трех, оно является следствием предложения four_sides из инварианта класса RECTANGLE, которое требует, чтобы сторон было ровно четыре.
Наследование и конструкторы
Ранее не показанная процедура создания (конструктор) для класса POLYGON может иметь вид
make_polygon (vl: LINKED_LIST [POINT]) is
-- Создание по вершинам из vl.
require
vl.count >= 3
do
...Инициализация представления многоугольника по элементам из vl ...
ensure
-- vertices и vl состоят из одинаковых элементов (это можно выразить
формально)
endЭта процедура берет список точек, содержащий по крайней мере три элемента, и использует его для создания многоугольника.
| Ей дано собственное имя make_polygon, чтобы избежать конфликта имен при ее наследовании классом RECTANGLE, у которого имеется собственная процедура создания make. Мы не рекомендуем так делать в общем случае, в следующей лекции будет показано, как давать процедуре создания класса POLYGON стандартное имя make, а затем использовать переименование в предложении о наследовании класса RECTANGLE, чтобы предотвратить коллизию имен. |
Приведенная выше процедура создания класса RECTANGLE имеет четыре аргумента: точку, служащую центром, длины двух сторон и ориентацию. Отметим, что компонент vertices применим к прямоугольникам, поэтому процедура создания для RECTANGLE создает список вершин vertices (четыре угла вычисляются по центру, длинам сторон и ориентации).
Общая процедура создания для многоугольников не удобна прямоугольникам, так как приемлемы только списки из четырех элементов, удовлетворяющих инварианту класса RECTANGLE. Процедура создания для прямоугольников, в свою очередь, не годится для произвольных многоугольников. Это обычное дело: процедура создания родителя не подходит для наследника. Нельзя гарантировать, что она будет удовлетворять его новому инварианту.
Например, если у наследника имеются новые атрибуты, то процедуре создания нужно будет их инициализировать, для чего потребуются дополнительные аргументы. Отсюда общее правило:
Правило наследования конструктора
При наследовании свойство процедуры быть конструктором не сохраняется.
Наследуемая процедура создания все еще доступна в наследнике, как и любой другой компонент родителя, но она не сохраняет статус конструктора. Этим статусом обладают только процедуры, перечисленные в предложении creation наследника.
В некоторых случаях родительский конструктор подходит и для наследника. Тогда его просто нужно указать в предложении creation:
class B inherit
A
creation
make
feature
...где процедура make наследуется без изменений от класса A, у которого она также указана в предложении creation.
Пример иерархии
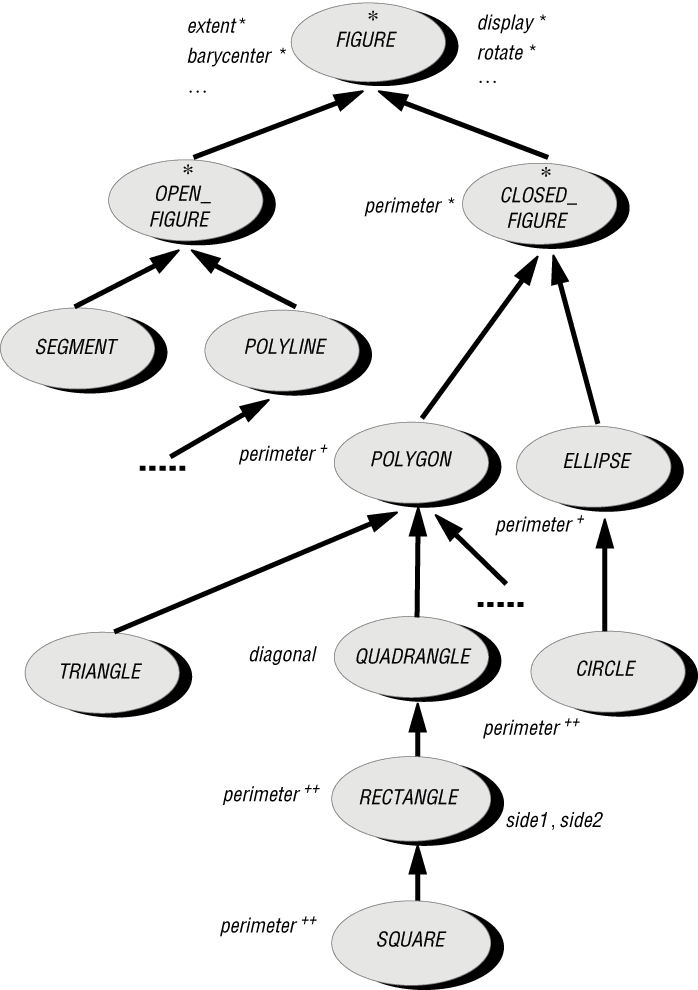
В конце обсуждения полезно рассмотреть пример POLYGON-RECTANGLE в контексте более общей иерархии типов геометрических фигур.
Фигуры разбиты на замкнутые и незамкнутые. Примером замкнутой фигуры кроме многоугольника является также эллипс, а частным случаем эллипса является круг.
Рядом с классами указаны их разные компоненты. Символ " ++ " означает "переопределено", а символы " + " и " * " будут объяснены далее.
Ранее для простоты RECTANGLE был наследником класса POLYGON. Поскольку указанная классификация основана на числе вершин, то представляется разумным ввести промежуточный класс QUADRANGLE для четырехугольников на том же уровне, что и классы TRIANGLE, PENTAGON и т. п. Тогда компонент diagonal (диагональ) можно переместить на уровень класса QUADRANGLE.
Отметим, что класс SQUARE, наследник класса RECTANGLE, характеризуется инвариантом side1 = side2. Аналогично, у эллипса имеются два фокуса, а у круга они сливаются в один, что определяет инвариант класса CIRCLE: equal (focus1 = focus2).