| Высшее образование |
Теоретические основы правовой информатики
Рассмотрим основные теоретические понятия и факты информатики, на которых базируется и правовая информатика.
Сообщения измеряются в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах, петабайтах и эксабайтах, реализуются в ЭВМ в битах.
Основные соотношения между единицами измерения сообщений: 1 бит (binary digit – двоичная единица) = 0 или 1; 1 байт = 8 битов; 1 килобайт (1К) = 213 бит; 1 мегабайт (1М) = 223 бит; 1 гигабайт (1Г) = 233 бит; 1 терабайт (1Т) = 243 бит; 1 петабайт (1П) = 253 бит; 1 эксабайт (1Э) = 263 бит.
Код – правило соответствия набора знаков одного множества  знакам другого множества
знакам другого множества  . Если каждому символу
. Если каждому символу  при кодировании соответствует отдельный знак
при кодировании соответствует отдельный знак  , то это кодирование. Если для каждого символа из
, то это кодирование. Если для каждого символа из  найдется по некоторому правилу однозначно его прообраз в
найдется по некоторому правилу однозначно его прообраз в  , то это правило называется декодированием.
, то это правило называется декодированием.
Кодирование – процесс преобразования букв (слов) алфавита  в буквы (слова) алфавита
в буквы (слова) алфавита  .
.
При представлении сообщений в ЭВМ все символы кодируются байтами (например, стандарт кодирования ASCII) или двумя байтами (стандарт UNICOD).
Сообщение, которое мы хотим передать адресату, назовем открытым сообщением. Зашифрованное сообщение – закрытое сообщение.
Процесс преобразования открытого сообщения в закрытое сообщение и есть шифрование. Если  – открытое сообщение,
– открытое сообщение,  – закрытое сообщение (шифр),
– закрытое сообщение (шифр),  – правило шифрования, то имеется зависимость вида:
– правило шифрования, то имеется зависимость вида: 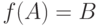 .
.
Правила шифрования должны быть выбраны так, чтобы зашифрованное сообщение можно было бы расшифровать. Однотипные правила объединяются в классы правил и внутри класса определяется некоторый параметр, позволяющий перебирать все такие правила.
Этот параметр называется шифровальным ключом. Ключ, как правило, секретный и сообщается лишь тому, кто должен прочесть зашифрованное сообщение (обладателю ключа).
При кодировании нет такого секретного ключа, так как кодирование ставит целью лишь более сжатое, компактное представление сообщения.
Если  – ключ, то можно записать
– ключ, то можно записать 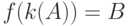 . Для каждого ключа
. Для каждого ключа  , преобразование
, преобразование 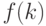 должно быть обратимым, то есть
должно быть обратимым, то есть  . Совокупность преобразования
. Совокупность преобразования 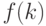 и соответствия множества
и соответствия множества  называется шифром.
называется шифром.
Принцип Кирхгоффа: секретность зашифрованных сообщений определяется секретностью ключа.
Это означает, что если даже алгоритм шифрования будет известен криптоаналитику, тот, тем не менее, не в состоянии будет расшифровать закрытое сообщение, если не располагает соответствующим ключом.
В российских и американских шифрах часто используется  -битовый ключ, а число различных ключей (пространство ключей) составляет при этом
-битовый ключ, а число различных ключей (пространство ключей) составляет при этом  .
.
Для измерения количества информации используются различные подходы и методы.
Количество информации – число, адекватно характеризующее структурированность, определенность в оцениваемой системе.
Количество информации часто оценивается в битах.
Рассмотрим меру информации по Р. Хартли.
Пусть известны  состояний системы
состояний системы  (
(  опытов с различными, равновозможными, последовательными состояниями системы). Мера разнообразия множества состояний системы задается формулой Р. Хартли:
опытов с различными, равновозможными, последовательными состояниями системы). Мера разнообразия множества состояний системы задается формулой Р. Хартли:

Если во множестве 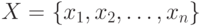 искать произвольный элемент, то для его нахождения (по Хартли) необходимо иметь не менее
искать произвольный элемент, то для его нахождения (по Хартли) необходимо иметь не менее 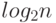 (бит) информации.
(бит) информации.
Уменьшение  говорит об уменьшении разнообразия состояний
говорит об уменьшении разнообразия состояний  системы. Увеличение
системы. Увеличение  говорит об увеличении разнообразия состояний
говорит об увеличении разнообразия состояний  системы.
системы.
Мера Хартли подходит лишь для идеальных систем, так как в реальных системах состояния системы обычно не одинаково осуществимы (не равновероятны).
Для реальных систем используют более подходящую меру К. Шеннона. Мера Шеннона оценивает информацию отвлеченно от ее смысла:
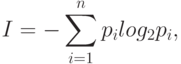
где  – число состояний системы;
– число состояний системы; 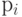 – вероятность (относительная частота) перехода системы в
– вероятность (относительная частота) перехода системы в  -ое состояние, а сумма всех
-ое состояние, а сумма всех 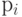 должна равняться
должна равняться  .
.
Если все состояния рассматриваемой системы равновозможны, равновероятны, то есть 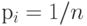 , то из формулы Шеннона можно получить (как частный случай) формулу Хартли:
, то из формулы Шеннона можно получить (как частный случай) формулу Хартли:

В термодинамике известен так называемый коэффициент Больцмана 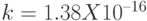 (эрг/град) и формула Больцмана для энтропии или меры хаоса в термодинамической системе:
(эрг/град) и формула Больцмана для энтропии или меры хаоса в термодинамической системе:
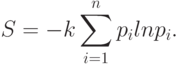
Сравнивая выражения для  и
и  можно заключить, что величину I можно понимать как энтропию из-за нехватки информации в системе (о системе).
можно заключить, что величину I можно понимать как энтропию из-за нехватки информации в системе (о системе).
