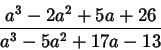| При задании различных оттенков цвета при кодировании графической информации, широко применяется следующая система счисления: |
Системы компьютерной алгебры
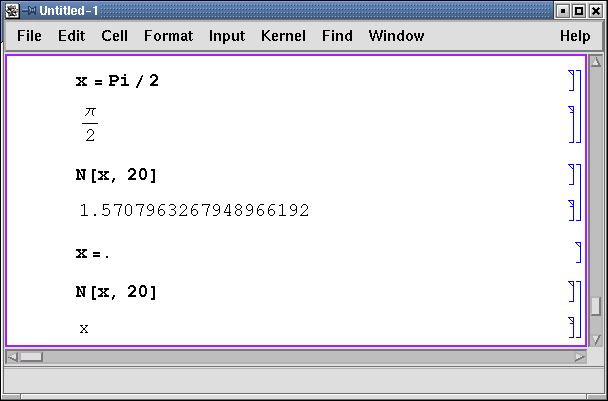
Mathematica допускает использование чисел четырех видов: целые, рациональные, вещественные и комплексные. Все типы чисел могут содержать любое количество цифр. Чтобы число рассматривалось как вещественное, оно должно содержать точку в его записи, даже если дробная часть равна нулю, например, 2. или 2.0.
Для перевода числа, заданного в системе счисления с произвольным основанием, в десятичную используется конструкция Основание^^Число, а для обратного перевода числа a из десятичной системы в систему с основанием n (где n не превышает 32) - функция BaseForm[a, n].
Инициализация переменных осуществляется при помощи операции =, для аннулирования значения переменной следует после знака равно указать символ . (точка).
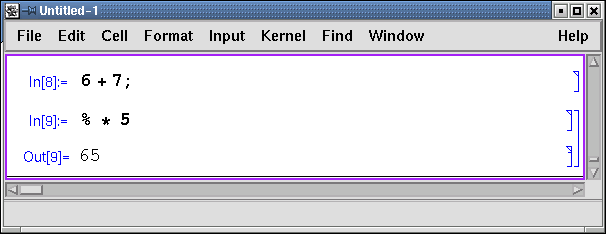
При выполнении вычислений особая роль отводится символу % - он означает результат предыдущей операции. Комбинация символов %% соответствует результату операции, выполненной перед предыдущей, и так далее.
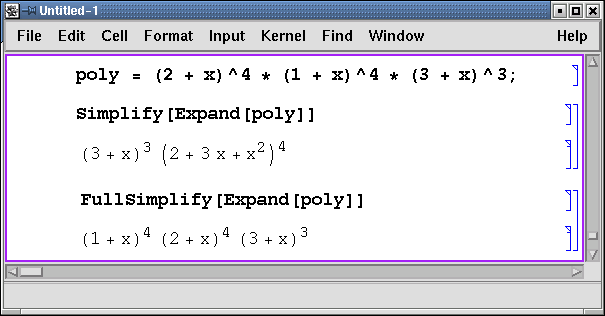
Для того чтобы "заставить" систему упростить выражение, используется функция Simplify. Ниже приведены примеры использования этой функции.
Функция Expand раскрывает скобки в выражении. Например, в результате выполнения команды Expand[(a + b)3] получится a3 + 3a2b + 3ab2 + b3.
К сожалению, функция Simplify не всегда выдает самый простой результат. В этом случае можно использовать функцию FullSimplify.
В этом примере мы сначала завели переменную poly для хранения многочлена, что позволило в дальнейшем избежать его повторного ввода. Упрощение результата раскрытия скобок не приводит к исходному выражению, которое получается только после применения функции FullSimplify.
Обратите внимание на символ ; (точка с запятой) в конце ввода многочлена. Этот символ препятствует выводу на экран результата обработки программой Mathematica введенного выражения.
Разложение на множители, если это возможно, осуществляет функция Factor. Эта функция может работать и с тригонометрическими выражениями, но в этом случае нужно использовать дополнительную опцию Trig -> True:
In[10]:= Factor[x^4+8x^3+17x^2+16x+30]
Out[10]= (3 + x)(5 + x)(2 + x^2)
In[11]:= Factor[Sin[6x]/Sin[2x] + Cos[6x - Pi]/Cos[2x],
Trig -> True]
Out[11]= 2Напомним, это многочленом P(x)степени n от переменной x называется выражение вида
a0xn+a1xn-1+...+ an-1x+an.
Для вынесения общего числового множителя в многочлене за скобки предназначена функция FactorTerms[poly, x], где poly есть многочлен от переменной x. Для получения списка коэффициентов при степенях x, начиная с нулевой, используется функция CoefficientList[poly, x].
In[12]:= FactorTerms[1232x^4+168x+144, x]
Out[12]= (8 ((18 + 21x + 154x^4))
In[13]:= CoefficientList[12x^4+68x+44,x]
Out[13]= {44,68,0,0,12}Некоторые другие функции для работы с многочленами приведены в следующей таблице.
| PolynomialGCD[poly1, poly2] | Нахождение наибольшего общего делителя poly1 и poly2 |
| PolynomialLCM[poly1, poly2] | Нахождение наименьшего общего кратного |
| PolynomialQuotient[poly1, poly2, x] | Нахождение частного от деления poly1 на poly2 |
| PolynomialRemainder[poly1, poly2, x] | Нахождение остатка от деления poly1 на poly2 |
Пример
Пусть P1(x)= x4+2x3-4x2-5x-6. Определим, является ли число 2 корнем уравнения P1(x)=0. Известно, что многочлен делится без остатка на выражение x-x0, где x0 - корень уравнения. Найдем остаток от деления P1(x) на x-2:
PolynomialRemainder[x^4+2x^3-4x^2-5x-6, x-2 , x].
Результат равен 0, следовательно 2 - корень данного уравнения.
Задания
- Вычислитe 2-10 с точностью 20 знаков после запятой.
- Упростите выражение
- Разложите на множители выражение
x6-18x5+135x4-540x3+ 1215x2-1458x+729
. - Найдите остаток от деления многочлена P1(x) на x-1