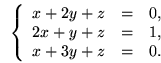| При задании различных оттенков цвета при кодировании графической информации, широко применяется следующая система счисления: |
Преподаватель
Вы можете этот курс.
Опубликован: 27.07.2006 | Уровень: для всех | Доступ: свободно
Лекция 8:
Системы компьютерной алгебры
Матричные вычисления
Maxima позволяет легко манипулировать матрицами. В следующем примере задаются две матрицы, которые затем складываются (+) и перемножаются (.):
(C1) A:matrix([1,2],[3,4]); [ 1 2 ] (D1) [ ] [ 3 4 ] (C2) B:matrix([1,1],[1,1]); [ 1 1 ] (D2) [ ] [ 1 1 ] (C3) A + B; [ 2 3 ] (D3) [ ] [ 4 5 ] (C4) A . B; [ 3 3 ] (D4) [ ] [ 7 7 ]
Функция determinant вычисляет определитель матрицы.
(C5) determinant(A); (D5) - 2 (C6) determinant(matrix([a,b],[c,d])); (D6) a d - b c
Транспонирование матрицы осуществляется функцией transpose.
(C7) transpose(A); [ 1 3 ] (D7) [ ] [ 2 4 ]
Для получению обратной матрицы используется операция ^^-1 или функция invert.
(C8) A^^-1;
[ - 2 1 ]
[ ]
(D8) [ 3 1 ]
[ - - - ]
[ 2 2 ]
(C9) invert(A);
[ - 2 1 ]
[ ]
(D9) [ 3 1 ]
[ - - - ]
[ 2 2 ]Как известно, каждый элемент bij обратной матрицы B = A-1 получается делением алгебраического дополнения Aij соответствующего элемента исходной матрицы на ее определитель |A|. Для того чтобы вынести 1/|A| в качестве сомножителя применяется функция detout.
(C10) invert(A), detout; [ 4 - 2 ] [ ] [ - 3 1 ] (D10) - ------------ 2
Убедимся в правильности полученного результата, умножив A на обратную к ней матрицу:
(C11) A . d9; [ 1 0 ] (D11) [ ] [ 0 1 ]
Будьте внимательны: в результате выполнения операции ^-1 получится матрица, каждый элемент которой обратен элементу исходной, а не обратная матрица.
(C12) A^-1; [ 1 ] [ 1 - ] [ 2 ] (D12) [ ] [ 1 1 ] [ - - ] [ 3 4 ]
Использование матриц позволяет легко решать системы линейных уравнений с несколькими переменными. Пусть A - матрица коэффициентов системы, X - матрица неизвестных, B - матрица свободных членов системы. Тогда матрица X находится по формуле X = A -1 . B, где операция . означает матричное умножение.
Пример
Решим следующую систему уравнений матричным способом.
Сначала заполним соответствующие матрицы, а затем получим матрицу результатов:
(C14) A:matrix([1, 2, 1], [2, 1, 1], [1, 3, 1]); [ 1 2 1 ] [ ] (D14) [ 2 1 1 ] [ ] [ 1 3 1 ] (C15) B:matrix([0, 1, 0]); (D15) [ 0 1 0 ] (C16) (A^^-1).B; [ 1 ] [ ] (D16) [ 0 ] [ ] [ - 1 ]
Задания
- Вычислите произведение матриц A.B и B.A, где
- Найдите определители матриц C и D
- Для матрицы D найдите обратную, после чего проверьте, что в результате их произведения получается единичная матрица.
- Решите следующую систему уравнений матричным способом
Программирование в системе Maxima
До сих пор мы использовали систему Maxima в интерактивном режиме, подобно калькулятору. Если часто приходится выполнять определенную последовательность вычислений, то лучше оформить ее в виде программы, которая затем вызывается в случае надобности. Ниже приводится небольшая программа для нахождения критических точек функции f(x). Пользователю предлагается ввести функцию f, после чего вычисляется производная введенной функции и при помощи функции solve решается уравнение fx = 0. Программа записывается в текстовый файл и затем загружается в систему Maxima при помощи функции batch. Приведем текст программы:
/* -----------------------------------------------------
Это файл critpoints.max:
(Maxima использует комментарии в стиле C)
-------------------------------------------------- */
critpts():=(
print("Программа нахождения критических точек"),
/* Запрос на ввод функции */
print("Введите функцию f(x):"),
f:read(),
/* Печать введенной функции (для контроля) */
print("f = ",f),
/* В переменную eq помещаем значение производной */
eq:diff(f,x),
/* Решаем уравнение */
solve(eq, x)
)$Программа состоит из единственной функции (без аргументов), которая называется critpts. Команды отделяются друг от друга запятыми. Вот пример выполнения программы:
(C1) batch("critpoints.max");
batching #p/home/test/critpoints.max
(C2) critpts() := (PRINT("Программа #
нахождения критических точек"),
PRINT("Введите функцию f(x):"),
f : READ(),
PRINT("f = ", f),
eq : DIFF(f, x),
SOLVE(eq, x))
(C3) critpts() ;
Программа нахождения критических точек
Введите функцию f(x):
(x+2)/(x^2+1);
x + 2
f = ------
2
x + 1
(D3) [x = - SQRT(5) - 2, x = SQRT(5) - 2]
