| Экстернат |
Криптографические хэш-функции
2.2. SHA-512
версия SHA (Secure Hash Algorithm) - алгоритм безопасного хэширования с 512-битовым дайджестом сообщения. Эта версия похожа на другие алгоритмы этого семейства, которые основаны на схеме Меркеля-Дамгарда. Мы выбрали для рассмотрения особую версию. Она самая поздняя, обладает более полной структурой, чем другие, и наиболее длинным дайджестом сообщения. Если понять эту версию, нетрудно будет усвоить структуру других версий.
Введение
SHA-512 создает дайджест из сообщения, содержащего много блоков. Каждый блок имеет длину 1024 бита, как это показано на рис. 2.6.
Дайджест вначале устанавливается на определенное заранее значение 512 битов. Алгоритм смешивает это начальное значение с первым блоком сообщения, чтобы создать первый промежуточный дайджест сообщения 512 битов. Этот дайджест затем смешивается со вторым блоком, чтобы создать второй промежуточный дайджест. Наконец, (N - l) -ый дайджест смешивается с N -ым блоком - они создают N -ый дайджест. Когда последний блок обработан, результирующий дайджест - это дайджест полного сообщения.
Подготовка сообщения
SHA-512 требует, чтобы длина первоначального сообщения была меньше, чем 2128 битов. Если длина сообщения равна или больше, чем 2128, оно не будет обработано SHA-512. Это обычно не проблема, потому что 2128 битов превосходят возможную сегодня полную емкость хранения любой системы.
Пример 2.1
Этот пример показывает, что ограничение длины сообщения SHA-512 - не серьезная проблема. Предположим, что мы должны передать сообщение длиною 2128 бита в секунду. Какое время потребуется для системы коммуникаций со скоростью передачи данных 264 бита в секунду, чтобы передать это сообщение?
Решение
Системы коммуникаций, которая может передать 264 бита в секунду, пока еще не существует. Даже если бы она была, потребовалось бы много лет, чтобы передать это сообщение. Отсюда ясно, что мы не должны волноваться по поводу ограничения длины сообщения для SHA-512.
Пример 2.2
Этот пример также касается длины сообщения в SHA-512. Сколько страниц занимает сообщение 2128 бит?
Предположим, что символ имеет длину 32 или 26 бит. Каждая страница - меньше, чем 2048, или приблизительно 212, символов. Тогда 2128 битов требуют по крайней мере 2128/218, или 2110 страниц. И снова ясно, что мы не должны волноваться об ограничении на длину сообщения.
Поле длины и заполнение
Прежде чем дайджест сообщения может быть создан, SHA-512 требует сложения поля длины - это целое число без знака на 128 битов, которое определяет длину сообщения в битах, - с сообщением. Это длина первоначального сообщения перед заполнением. Поле целого числа без знака 128 битов можно определить как число между 0 и 2128 - 1, которое является максимальной длиной сообщения, принятого в SHA-512. Поле длины определяет длину первоначального сообщения перед его сложением или заполнением (рис. 2.7).
Перед сложением поля длины мы должны дополнить первоначальное сообщение, чтобы сделать длину кратной 1024. Для поля длины резервируется 128 битов, как показано на рис. 2.7. Длина области заполнения может быть рассчитана следующим образом. Пусть |M| - длина первоначального сообщения и |P| - длина поля заполнения.
( M + P + 128) = 0 mod 1024 -> P = (- M - 128) mod 1024
Формат заполнения - это одна 1, сопровождаемая необходимым числом нулей (0).
Пример 2.3
Какое число битов заполнения необходимо, если длина первоначального сообщения - 2590 битов?
Решение
Мы можем вычислить число битов заполнения следующим образом:
P = (-2590 -128) mod 1024 = -2718 mod 1024 = 354
Заполнение состоит из одной 1, сопровождаемой 353 нулями.
Пример 2.4
Нужно ли заполнение, если длина первоначального сообщения уже кратна 1024 битам?
Решение
Да, нужно, потому что мы должны добавить поле длины. Заполнение необходимо, чтобы сделать и новый блок кратным 1024 битам.
Пример 2.5
Каково минимальное и максимальное число битов заполнения, которые можно добавить к сообщению?
Решение
Минимальная длина заполнения - 0, и это случается, когда (-M - 128) mod 1024 = 0 ; тогда |M| = -128 mod 1024 = 896 mod 1024 бит. Другими словами, последний блок в первоначальном сообщении - 896 битов. Мы добавляем поле длины на 128 битов, чтобы сделать блок полным.
Максимальная длина заполнения - 1023, и это случается, когда (- M - 128) = 1023 mod 1024. Это означает, что длина первоначального сообщения - M = (-128 - 1023) mod 1024 или M = 897 mod 1024. В этом случае мы не можем просто добавить область длины, потому что длина последнего блока будет превышать на один бит число 1024. Так что мы нуждаемся в заполнении 127 битами, чтобы закончить этот блок и создать второй блок заполнения 896 битов. Теперь можно добавить поле длины, чтобы сделать этот блок полным.
Слова
SHA-512 оперирует словами; он - ориентируемый на слово. Слово определено длиной 64 бита. Это означает, что после того как заполнение и поле длины добавляются к сообщению, каждый блок сообщения состоит из шестнадцати слов по 64 бита. Дайджест сообщения также образуется из слов по 64 бита, но дайджест сообщения - только восемь слов, и слова обозначают A, B, C, D, E, F, G и H, как показано на рис. 2.8.
Расширение слова
Перед обработкой каждый блок сообщения должен быть расширен. Блок образован из 1024 битов, или шестнадцати слов по 64 бита. Как мы увидим позже, в фазе обработки нам нужно 80 слов. Так что блок с 16-ю словами должен быть расширен до 80 слов от W0 до W79. рис. 2.9 показывает процесс расширения слова. Блок на 1024 бита порождает первые слова; остальная часть слов получается от уже сделанных слов согласно операциям, которые показаны на рисунке.
Пример 2.6
Показать, как получить W60.
Решение
Каждое слово в диапазоне W16 до W79 получено в результате обработки четырех слов, созданных предварительно на предыдущих шагах. W60 получено как
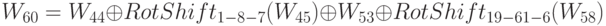
Инициализация дайджеста сообщения
Алгоритм использует восемь констант для инициализации дайджеста сообщения. Мы обозначаем их от A0 до H0, что соответствует обозначению слов, используемых для дайджеста. табл. 2.2 показывает значение этих констант.
Читатель может задаться вопросом, откуда взяты эти значения. Они рассчитаны из первых восьми простых чисел (2, 3, 5, 7, 11, 13, 17 и 19). Каждое значение - дробная часть квадратного корня соответствующего простого числа после преобразования к двоичной форме и сохранения только первых 64 битов. Например, восьмое простое число - 19 имеет квадратный корень (191/.2) = 4,35889894354. Преобразовывая число к двоичной форме только с 64 битами в дробной части, мы имеем
(100.0101 1011 1110... 1001)2 -> (4,5BEOCD19137E2179)16
SHA-512 сохраняет дробную часть (5BEOCD19137E2179)16 как целое число без знака.




