| Стоимость "обучения" |
Преподаватель
Вы можете этот курс.
Опубликован: 20.04.2011 | Уровень: для всех | Доступ: свободно
Лекция 11:
Многомерные системы с потерями
Аннотация: В этой лекции мы обобщаем классическую теорию телетрафика на решение задач в мультисервисных системах (например, цифровые сети интегрального обслуживания ISDN и B ISDN ). Каждый класс услуг соответствует потоку нагрузки. Несколько потоков нагрузки предлагаются одной и той же группе пучков каналов.
В секции 10.1 мы рассматриваем классическую многомерную B-формулу потерь Эрланга. Это пример обратимого марковского процесса, который мы рассмотрим более детально в секции 10.2. В секции 10.3 мы проанализируем большее количество общих систем с потерями и стратегий, включая сервисную защиту (максимальное распределение каналов между сервисами) и мультислотовую нагрузку ( BPP ). Все модели имеют так называемую мультипликативную форму (форму произведения - product form ), и их числовая оценка очень упрощается при использовании алгоритма свертки для систем с потерями, реализованных специальной программой (секция 10.4). В секции 10.5 будут приведены другие алгоритмы для решения этой проблемы.
Все модели, которые мы рассматриваем, основаны на гибком распределении каналов/слотов. Они могут быть обобщены на произвольные сети коммутации каналов с прямой маршрутизацией, где мы вычисляем вероятности блокировки из конца в конец (Лекция 11). Все модели нечувствительны к распределению времени обслуживания, и таким образом они устойчивы для приложений. В конце лекции поговорим о других алгоритмах.
Ключевые слова: PCT, состояние системы, диаграмма, система без потерь, пуассоновское распределение, константы, среднее время, ПО, суперпозиция, распределение времени, вероятность, поток, путь, BPP, Паскаль, основание, класс, PABX, обобщение, алгоритм, Биноминальное распределение, пространство, запись
Многомерная B-формула Эрланга
Мы рассматриваем группу n пучков каналов (каналы, слоты), которым предлагают два независимых PCT-I потока нагрузк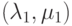и: 
и 
. Предлагаемая нагрузка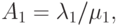 
соответственно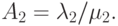 
Обозначим состояние системы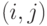 
, где 
- число вызовов от потока 1, а 
- число вызовов от потока 2. Выполняются следующие ограничения:
 |
( 10.1) |
Диаграмма переходов состояний показана на рис.10.1. Согласно предположению о статистическом равновесии, вероятности состояний могут быть получены решением глобальных уравнений равновесия для каждого узла (уравнения узла), всего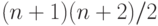 
уравнения.
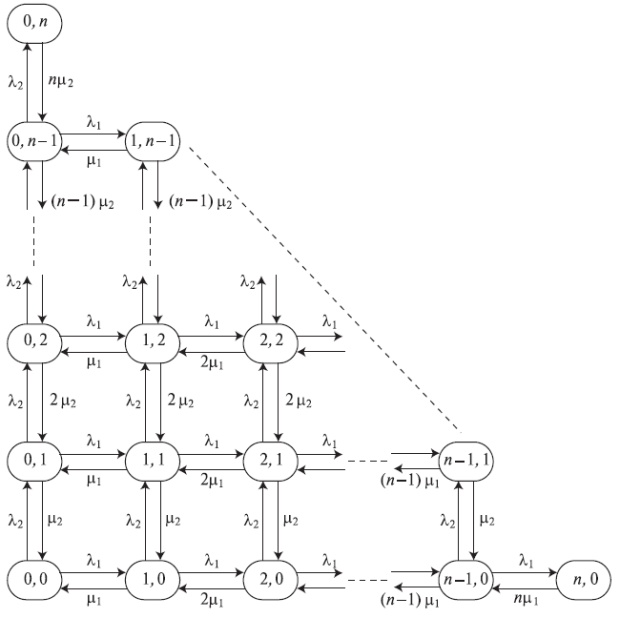
Рис. 10.1. Двухмерная диаграмма переходов состояний для системы с потерями с n каналами, которым предлагают два PCT- I потока нагрузки.
Это эквивалентно диаграмме переходов состояний для системы с потерями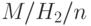 
, где гиперэкспоненциальное распределение 
дается в (10.7)
Как мы увидим в следующей секции, эта диаграмма соответствует обратимому марковскому процессу, который имеет локальное равновесие и, кроме того, решение имеет форму произведения ( product form ). Мы можем легко показать, что глобальные уравнения равновесия удовлетворяют следующим вероятностям состояния, которые могут быть записаны в форме произведения:
 |
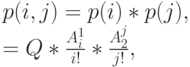( 10.2) |
где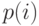 
и 
- одномерные усеченные Пуассоновские распределения, Q - нормировочные константы, и 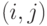выполняют вышеупомянутые ограничения (10.1). Поскольку рассматриваются Пуассоновские потоки вызовов, которые обладают свойством PASTA (Пуассоновское поступление вызовов, наблюдаемое за среднее время), потери по времени, потери по вызовам и потери по нагрузке равны между собой для обоих потоков нагрузки, и они равняются 
.
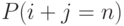Биноминальным разложением или сверткой двух Пуассоновских распределений мы находим следующие объединенные вероятности состояний, где 
получено нормализацией:
 |
( 10.3) |
 |
( 10.4) |
Это усеченное Пуассоновское распределение (7.9) с предложенной нагрузкой:
 |
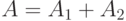( 10.5) |
Мы можем также интерпретировать эту модель как систему Эрланга с потерями с одним Пуассоновским потоком вызовов и гиперраспределенными временами пребывания в системе следующим образом. Полный процесс поступления вызовов - суперпозиция двух Пуассоновских процессов с полной интенсивностью поступления:
 |
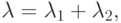( 10.6) |
и распределение времени пребывания в системе является гиперраспределенным:
 |
( 10.7) |
Мы присваиваем веса эти двум экспоненциальным распределениям согласно относительному числу вызовов в единицу времени. Среднее время обслуживания и распределение времени пребывания в системе является гиперраспределенным:
 |
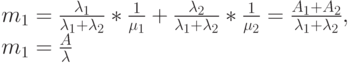( 10.8) |
и соответствует предложенной нагрузке.
Таким образом, мы показали, что система с потерями Эрланга справедлива для гиперраспределенных времен пребывания в системе.
Можно обобщить вышеупомянутую модель на 
потоков нагрузки:
 |
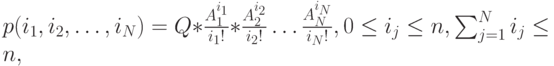( 10.9) |
Данная модель является общей многомерной B-формулой Эрланга. Обобщая (10.3), мы замечаем, что глобальные вероятности состояния могут быть вычислены следующей рекурсией, где q(x) обозначает вероятность относительного состояния, и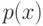 
- абсолютные вероятности состояния:
 |
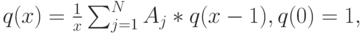( 10.10) |
 |
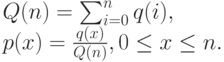( 10.11) |
Если использовать рекурсию с нормированием (секция 7.4), то мы получаем рекурсивную формулу B- Эрланга. Формула (10.10) подобна уравнениям равновесия для Пуассоновского случая, когда:
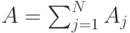
Потери по времени -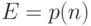 
, и в соответствии со свойствами потока PASTA, потери по времени также равны потерям по вызовам и по нагрузке. Числовые оценки мы рассмотрим в секции 10.4. Многомерные системы были сначала упомянуты Эрлангом и более тщательно рассмотрены Иенсоном в Erlangbook (Jensen, 1948 ).
