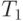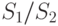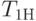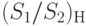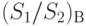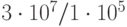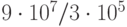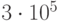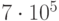| Высшее образование |
Планирование экспериментов
4.7. Точность и количество реализаций модели при определении вероятностей исходов
Мы рассматриваем случай, когда в качестве показателя эффективности выступает вероятность свершения (или не свершения) какого-либо события, например, поражения цели, выхода из строя техники, завершения комплекса работ в заданное время и др.
В качестве оценки вероятности  события
события  выступает частота его свершения:
выступает частота его свершения:
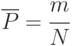
где  - число реализаций модели;
- число реализаций модели;
 - число свершений данного события.
- число свершений данного события.
Использование частоты 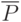 в качестве оценки искомой вероятности
в качестве оценки искомой вероятности  основано на теореме Я. Бернулли, которую в данном случае можно в формализованном виде записать так:
основано на теореме Я. Бернулли, которую в данном случае можно в формализованном виде записать так:
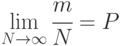
Точность и достоверность этой оценки связаны уже с известным определением достоверности:
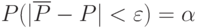
Задача сводится к нахождению такого количества реализаций 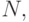 чтобы оценка
чтобы оценка 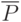 отличалась от искомого значения
отличалась от искомого значения  менее, чем на
менее, чем на  с заданной достоверностью. Здесь, как и ранее,
с заданной достоверностью. Здесь, как и ранее,  - абсолютное значение, характеризующее точность оценки.
- абсолютное значение, характеризующее точность оценки.
Для нахождения функциональной связи между точностью, достоверностью и числом реализаций модели введем переменную  - результат исхода
- результат исхода 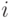 -й реализации модели:
-й реализации модели:
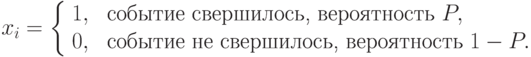
Тогда частота свершения события (оценка искомой вероятности) будет определяться следующим выражением:
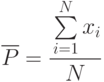
Величина 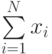 - случайная и дискретная. Она при таком задании
- случайная и дискретная. Она при таком задании  имеет биномиальное распределение (распределение Бернулли) с характеристиками:
имеет биномиальное распределение (распределение Бернулли) с характеристиками:
- матожидание
![M\left [\sum\limits_{i=1}^{N}{x_i}\right ]=NP](/sites/default/files/tex_cache/58a6978a7db6821b776dfefe246f2a57.png)
- дисперсия
![D\left [\sum\limits_{i=1}^{N}{x_i}\right ]=NP(1-P)](/sites/default/files/tex_cache/e504d328c9ae55c0744b68c9917e2679.png)
Из этого следует:
![M[\overline{P}]=M\left [\frac{\sum\limits_{i=1}^{N}{x_i}}{N}\right ]=\cfrac{1}{N}NP=P,\\
D[\overline{P}]=D\left [\frac{\sum\limits_{i=1}^{N}{x_i}}{N}\right ]=\cfrac{1}{N^2}NP(1-P)=
\cfrac{P(1-P)}{N},\\
\sigma_{\overline{P}}=\sqrt{D[\overline{P}]}=\cfrac{P(1-P)}{N}](/sites/default/files/tex_cache/52b5462cfef43297ac8063d068001523.png)
В теории вероятностей есть теорема Лапласа (частный случай центральной предельной теоремы), сущность которой состоит в том, что при больших значениях числа реализаций  биномиальное распределение достаточно хорошо согласуется с нормальным распределением.
биномиальное распределение достаточно хорошо согласуется с нормальным распределением.
Следовательно, можно записать:
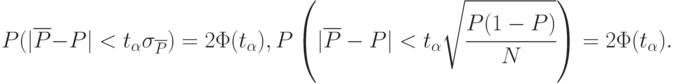
Следуя рассуждениям, приведенным ранее, получим искомые формулы:
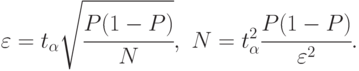
Как и ранее, 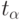 - аргумент функции Лапласа,
- аргумент функции Лапласа, 
Если априорные сведения хотя бы о порядке искомой вероятности  неизвестны, то использование значения абсолютной ошибки
неизвестны, то использование значения абсолютной ошибки  может не иметь смысла. Например, может быть так, что исследователь задал значение абсолютной ошибки
может не иметь смысла. Например, может быть так, что исследователь задал значение абсолютной ошибки 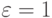 , а искомое значение вероятности оказалось
, а искомое значение вероятности оказалось 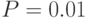 . Очевидно, явное несоответствие. Поэтому целесообразно оперировать относительной погрешностью:
. Очевидно, явное несоответствие. Поэтому целесообразно оперировать относительной погрешностью: 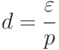
В этом случае формулы (4.5) принимают вид:
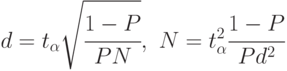
Из формул (4.6) следует, что при определении оценок малых вероятностей с приемлемо высокой точностью необходимо выполнить очень большое число реализаций модели. При отсутствии высокопроизводительного компьютера применение статистического моделирования становится проблематичным.
Определить число реализаций модели и затраты машинного времени для оценки данной вероятности с относительной точностью 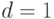 и достоверностью
и достоверностью 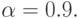 На выполнение одной реализации модели требуется 5 сек.
На выполнение одной реализации модели требуется 5 сек.
Решение
Из табл. 4.3 находим 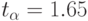 . Относительная точность
. Относительная точность 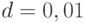 .
.
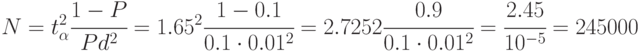
Если на выполнение одной реализации требуется 5 сек, то затраты машинного времени составят 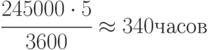
В формулах (4.5) и (4.6) для вычисления  или
или 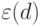 присутствует та же неопределенность, которую мы обсуждали ранее: вычисления требуют знания вероятности
присутствует та же неопределенность, которую мы обсуждали ранее: вычисления требуют знания вероятности  , а она до эксперимента неизвестна. Эта неопределенность снимается так.
, а она до эксперимента неизвестна. Эта неопределенность снимается так.
Выполняется предварительно 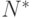 прогонов модели. Обычно
прогонов модели. Обычно 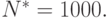 По данным этих прогонов вычисляют ориентировочное значение оценки вероятности
По данным этих прогонов вычисляют ориентировочное значение оценки вероятности 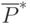 , которую и подставляют в формулу вместо вероятности
, которую и подставляют в формулу вместо вероятности  .
.
Если окажется  , моделирование следует продолжить до выполнения
, моделирование следует продолжить до выполнения  реализаций.
реализаций.
Если окажется  то моделирование заканчивается. При этом если
то моделирование заканчивается. При этом если 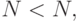 то следует определить действительную точность
то следует определить действительную точность  или
или  для
для  реализаций. Очевидно, в этом случае достигнутая точность будет выше заданной (ошибка меньше заданной)
реализаций. Очевидно, в этом случае достигнутая точность будет выше заданной (ошибка меньше заданной)
Но более удобно рассчитывать число реализаций на так называемый наихудший случай.
Вернемся к формуле (4.5)
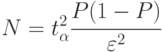
Анализ формулы показывает, что число реализаций модели в зависимости от вероятности  изменяется от
изменяется от  (при
(при  ) до
) до  (при
(при 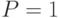 ), проходя через максимум. Максимальное значение
), проходя через максимум. Максимальное значение  принимает при
принимает при 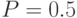 :
:
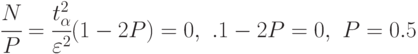
То есть наибольшее число реализаций модели будет тогда, когда искомая вероятность равна 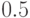 .
.
В этом случае число реализаций определяется так:
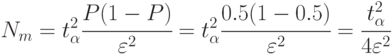
Если в результате моделирования окажется, что искомая вероятность значительно отличается от 0,5 (в любую сторону), то точность моделирования будет выше заданной (ошибка  меньше). Для определения этой точности следует воспользоваться уже известной формулой (4.5), но при
меньше). Для определения этой точности следует воспользоваться уже известной формулой (4.5), но при 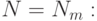
Пример 4.7. Сервер обрабатывает запросы, поступающие с автоматизированных рабочих мест (АРМ) с интервалами, распределенными по экспоненциальному закону со средним значением 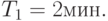 Вычислительная сложность запросов распределена по нормальному закону с математическим ожиданием
Вычислительная сложность запросов распределена по нормальному закону с математическим ожиданием 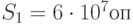 и среднеквадратическим отклонением
и среднеквадратическим отклонением 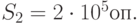 Производительность сервера по обработке запросов
Производительность сервера по обработке запросов 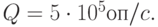
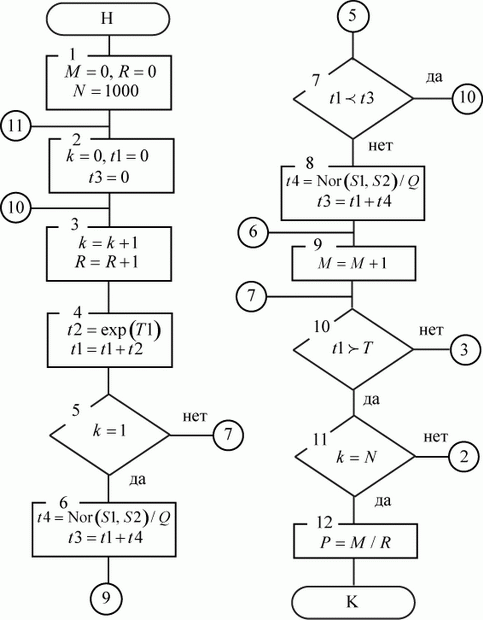
Построить алгоритм имитационной модели с целью определения вероятности обработки запросов за время 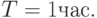 Исследовать зависимость вероятности обработки запросов от интервалов их поступления, вычислительной сложности и производительности сервера.
Исследовать зависимость вероятности обработки запросов от интервалов их поступления, вычислительной сложности и производительности сервера.
Решение
Для построения алгоритма имитационной модели введем следующие идентификаторы:
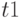 - текущее время поступления запроса;
- текущее время поступления запроса;
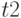 - интервал поступления запросов;
- интервал поступления запросов;
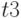 - текущее время окончания обработки запроса;
- текущее время окончания обработки запроса;
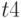 - время обработки запроса;
- время обработки запроса;
 - счетчик количества прогонов модели (реализаций);
- счетчик количества прогонов модели (реализаций);
 - вероятность обработки запросов;
- вероятность обработки запросов;
 - счетчик количества обработанных запросов;
- счетчик количества обработанных запросов;
 - заданное количество прогонов модели (реализаций);
- заданное количество прогонов модели (реализаций);
 - количество запросов за
- количество запросов за  прогонов модели;
прогонов модели;
 - время моделирования.
- время моделирования.
Алгоритм модели приведен на рис. 4.2.
Выберем интервалы варьирования уровней факторов.
 - средний интервал поступления запросов.
- средний интервал поступления запросов.
Для изменения математического ожидания и среднеквадрати-ческого отклонения целесообразно ввести коэффициент, принимающий два значения, например,  и
и  . Тогда
. Тогда  ,
, 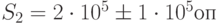 ,
, 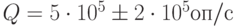 - производительность сервера.
- производительность сервера.
В соответствии с интервалами варьирования представим уровни факторов таблицей (табл. 4.5). В табл. 4.5 индексы н и в - нижний и верхний уровни факторов соответственно.
Составим план факторного эксперимента:
| № |  |
|
 |
 |
|
|---|---|---|---|---|---|
 |
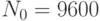 |
||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | -1 | -1 | -1 | 0.375 | 0.375 |
| 2 | -1 | -1 | +1 | 0.584 | 0.583 |
| 3 | -1 | +1 | -1 | 0.166 | 0.167 |
| 4 | -1 | +1 | +1 | 0.32 | 0.319 |
| 5 | +1 | -1 | -1 | 0.64 | 0.642 |
| 6 | +1 | -1 | +1 | 0.809 | 0.808 |
| 7 | +1 | +1 | -1 | 0.376 | 0.375 |
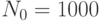
Проведем эксперимент. Выполним первое наблюдение при  прогонов модели. Получим вероятность обработки запросов
прогонов модели. Получим вероятность обработки запросов 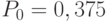 . Занесем ее в табл. 4.5 (строка 1, столбец 5) Зададимся точностью
. Занесем ее в табл. 4.5 (строка 1, столбец 5) Зададимся точностью 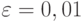 и доверительной вероятностью
и доверительной вероятностью 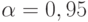 . По таблице значений функции Лапласа найдем ее аргумент
. По таблице значений функции Лапласа найдем ее аргумент  (см. табл. 4.3).
(см. табл. 4.3).
Рассчитаем требуемое количество прогонов модели при 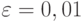 и
и 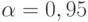 :
:
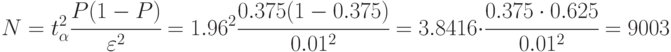
При расчете числа прогонов для "худшего случая" (а такой вариант возможен, так как в табл. 4.6 мы видим, что есть  ) получим:
) получим: