| Высшее образование |
Понятие модели и моделирования
1.2.3. Классификация моделей и моделирования по признаку "способ реализации модели"
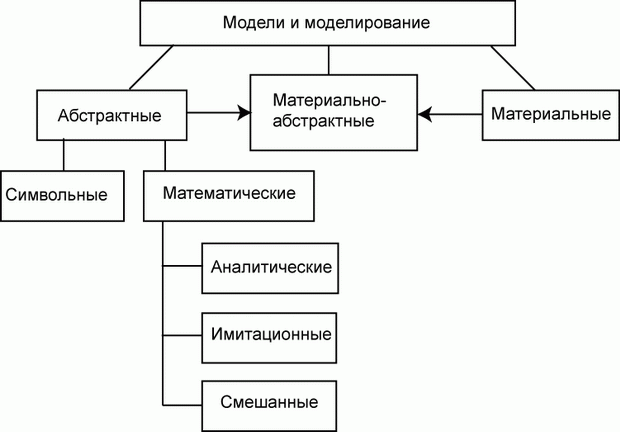
Согласно этому признаку модели делятся на два обширных класса:
- абстрактные (мысленные) модели;
- материальные модели.
Нередко в практике моделирования присутствуют смешанные, абстрактно-материальные модели.
Абстрактные модели представляют собой определенные конструкции из общепринятых знаков на бумаге или другом материальном носителе или в виде компьютерной программы.
Абстрактные модели, не вдаваясь в излишнюю детализацию, можно разделить на:
- символические;
- математические.
Символическая модель - это логический объект, замещающий реальный процесс и выражающий основные свойства его отношений с помощью определенной системы знаков или символов. Это либо слова естественного языка, либо слова соответствующего тезауруса, графики, диаграммы и т. п.
Символическая модель может иметь самостоятельное значение, но, как правило, ее построение является начальным этапом любого другого моделирования.
Математическое моделирование - это процесс установления соответствия моделируемому объекту некоторой математической конструкции, называемой математической моделью, и исследование этой модели, позволяющее получить характеристики моделируемого объекта.
Математическое моделирование - главная цель и основное содержание изучаемой дисциплины.
Математические модели могут быть:
- аналитическими;
- имитационными;
- смешанными (аналитико-имитационными).
Аналитические модели - это функциональные соотношения: системы алгебраических, дифференциальных, интегро-дифференциальных уравнений, логических условий. Уравнения Максвелла - аналитическая модель электромагнитного поля. Закон Ома - модель электрической цепи.
Преобразование математических моделей по известным законам и правилам можно рассматривать как эксперименты. Решение на основе аналитических моделей может быть получено в результате однократного просчета безотносительно к конкретным значениям характеристик ("в общем виде"). Это наглядно и удобно для выявления закономерностей. Однако для сложных систем построить аналитическую модель, достаточно полно отражающую реальный процесс, удается не всегда. Тем не менее, есть процессы, например, марковские, актуальность моделирования которых аналитическими моделями доказана практикой.
Имитационное моделирование. Создание вычислительных машин обусловило развитие нового подкласса математических моделей - имитационных.
Имитационное моделирование предполагает представление модели в виде некоторого алгоритма - компьютерной программы, - выполнение которого имитирует последовательность смены состояний в системе и таким образом представляет собой поведение моделируемой системы.
Процесс создания и испытания таких моделей называется имитационным моделированием, а сам алгоритм - имитационной моделью.
В чем заключается отличие имитационных и аналитических моделей?
В случае аналитического моделирования ЭВМ является мощным калькулятором, арифмометром. Аналитическая модель решается на ЭВМ.
В случае же имитационного моделирования имитационная модель - программа - реализуется на ЭВМ.
Имитационные модели достаточно просто учитывают влияние случайных факторов. Для аналитических моделей это серьезная проблема. При наличии случайных факторов необходимые характеристики моделируемых процессов получаются многократными прогонами (реализациями) имитационной модели и дальнейшей статистической обработкой накопленной информации. Поэтому часто имитационное моделирование процессов со случайными факторами называют статистическим моделированием.
Если исследование объекта затруднено использованием только аналитического или имитационного моделирования, то применяют смешанное (комбинированное), аналитико-имитационное моделирование. При построении таких моделей процессы функционирования объекта декомпозируются на составляющие подпроцессы, и для которых, возможно, используют аналитические модели, а для остальных подпроцессов строят имитационные модели.
Материальное моделирование основано на применении моделей, представляющих собой реальные технические конструкции. Это может быть сам объект или его элементы (натурное моделирование). Это может быть специальное устройство - модель, имеющая либо физическое, либо геометрическое подобие оригиналу. Это может быть устройство иной физической природы, чем оригинал, но процессы в котором описываются аналогичными математическими соотношениями. Это так называемое аналоговое моделирование. Такая аналогия наблюдается, например, между колебаниями антенны спутниковой связи под ветровой нагрузкой и колебанием электрического тока в специально подобранной электрической цепи.
Нередко создаются материально-абстрактные модели. Та часть операции, которая не поддается математическому описанию, моделируется материально, остальная - абстрактно. Таковы, например, командно-штабные учения, когда работа штабов представляет собой натурный эксперимент, а действия войск отображаются в документах.
Классификация по рассмотренному признаку - способу реализации модели - показана на рис. 1.2.
1.3. Этапы моделирования
Математическое моделирование как, впрочем, и любое другое, считается искусством и наукой. Известный специалист в области имитационного моделирования Роберт Шеннон так назвал свою широко известную в научном и инженерном мире книгу: "Имитационное моделирование - искусство и наука". Поэтому в инженерной практике нет формализованной инструкции, как создавать модели. И, тем не менее, анализ приемов, которые используют разработчики моделей, позволяет усмотреть достаточно прозрачную этапность моделирования.
Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь.
Обычно целями моделирования являются:
- прогноз поведения объекта при новых режимах, сочетаниях факторов и т. п.;
- подбор сочетания и значений факторов, обеспечивающих оптимальное значение показателей эффективности процесса;
- анализ чувствительности системы на изменение тех или иных факторов;
- проверка различного рода гипотез о характеристиках случайных параметров исследуемого процесса;
- определение функциональных связей между поведением ("реакцией") системы и влияющими факторами, что может способствовать прогнозу поведения или анализу чувствительности;
- уяснение сущности, лучшее понимание объекта исследования, а также формирование первых навыков для эксплуатации моделируемой или действующей системы.
Второй этап: построение концептуальной модели. Концептуальная модель (от лат. conception) - модель на уровне определяющего замысла, который формируется при изучении моделируемого объекта. На этом этапе исследуется объект, устанавливаются необходимые упрощения и аппроксимации. Выявляются существенные аспекты, исключаются второстепенные. Устанавливаются единицы измерения и диапазоны изменения переменных модели. Если возможно, то концептуальная модель представляется в виде известных и хорошо разработанных систем: массового обслуживания, управления, авторегулирования, разного рода автоматов и т. д. Концептуальная модель полностью подводит итог изучению проектной документации или экспериментальному обследованию моделируемого объекта.
Результатом второго этапа является обобщенная схема модели, полностью подготовленная для математического описания - построения математической модели.
Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения.
В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины.
Результатом третьего этапа моделирования является программа, составленная на наиболее удобном для моделирования и исследования языке - универсальном или специальном.
Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины.
Результат четвертого этапа - план эксперимента.
Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть.
Шестой этап: обработка, анализ и интерпретация данных эксперимента. В соответствии с целью моделирования применяются разнообразные методы обработки: определение разного рода характеристик случайных величин и процессов, выполнение анализов - дисперсионного, регрессионного, факторного и др. Многие из этих методов входят в системы моделирования (GPSS World, AnyLogic и др.) и могут применяться автоматически. Не исключено, что в ходе анализа полученных результатов модель может быть уточнена, дополнена или даже полностью пересмотрена.
После анализа результатов моделирования осуществляется их интерпретация, то есть перевод результатов в термины предметной области. Это необходимо, так как обычно специалист предметной области (тот, кому нужны результаты исследований) не обладает терминологией математики и моделирования и может выполнять свои задачи, оперируя лишь хорошо знакомыми ему понятиями.
На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин.
Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации.
Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание.
В-третьих, результат каждого из этапов должен являться самоценным продуктом. Например, концептуальная модель может и не использоваться для дальнейшего преобразования в математическую модель, а являться описанием, хранящим информацию о системе, которое может использоваться как архив, в качестве средства обучения и т. д.