| На каком этапе графического конвейера происходит отсечение невидимых объектов? |
Стратегии и критерии диспетчеризации процессов
Критерии диспетчеризации
Имеется пять основных критериев диспетчеризации процессора, которые так или иначе должны учитываться системой.
Использование процессора (CPU utilization) – поддержание его в режиме занятости максимально возможный период времени. Критерий оптимизации: максимизация данного показателя.
Пропускная способность системы (throughput) – (среднее) число процессов, завершающих свое выполнение за единицу времени. Критерий оптимизации: максимизация.
Время обработки процесса (turnaround time) – время, необходимое для исполнения какого-либо процесса. Критерий оптимизации: минимизация.
Время ожидания (waiting time) – время, которое процесс ждет в очереди процессов, готовых к выполнению. Критерий оптимизации: минимизация.
Время ответа (response time) – время, требуемое от момента первого запроса до первого ответа (данный показатель, как мы обсуждали ранее в лекции 1, наиболее важен для среды разделения времени). Критерий оптимизации: минимизация.
Как и при любой оптимизации, независимо от стратегии, удовлетворить всем критериям одновременно невозможно. Далее рассмотрим различные стратегии диспетчеризации и проанализируем их достоинства и недостатки, с точки зрения достижения оптимальности указанных критериев.
Стратегия First-Come-First-Served (FCFS)
Стратегия First-Come-First-Served (обслуживание в порядке поступления) – наиболее простая стратегия диспетчеризации, при которой ресурсы процессора предоставляются процессам в порядке их поступления (ввода) в систему, независимо от потребляемых ими ресурсов, в частности, от заявленного процессом времени, требуемого для его выполнения. При рассмотрении этой и других стратегий будем использовать диаграммы Ганта (Gantt charts изображающие имена процессов и временные диапазоны их выполнения, выраженные в некоторых единицах времени.
Рассмотрим следующий пример. Пусть процессы P1, P2 и P3 введены в систему в указанном порядке со следующими периодами активности:
Тогда при использовании стратегии FCFS для их диспетчеризации первым получит процессор первый процесс, несмотря на то, что он – наиболее долгий. Распределение процессора между процессами в данном случае изображено на рис. 11.3.
Таким образом, время ожидания для P1 = 0; P2= 24; P3 = 27.
Среднее время ожидания: (0 + 24 + 27)/3 = 17.
Если порядок процессов иной: P2 , P3 , P1 (последний введенный в систему процесс – самый долгий), то результат их диспетчеризации будет совершенно иным ( рис. 11.4).
Время ожидания процессов в данном случае: P1 = 6; P2 = 0; P3 = 3.
Среднее время ожидания: (6 + 0 + 3)/3 = 3
Данный результат много лучше, чем в предыдущем случае.
Эффект, продемонстрированный первым примером, носит название эффекта сопровождения (convoy effect) – увеличение среднего времени ожидания процессов в случаях, если короткий процесс обслуживается после долгого процесса.
Стратегия Shortest Job First (SJF)
Стратегия Shortest Job First (SJF, обслуживание самого короткого задания первым) – стратегия диспетчеризации процессора, при которой процессор предоставляется в первую очередь наиболее короткому процессу из имеющихся в системе.
В данном случае с каждым процессом связывается длина его очередного периода активности. Эта длина используется для того, чтобы первым обслужить самый короткий процесс .
Возможны две схемы применения данной стратегии:
- Без прерывания процессов – пока процессу предоставляется процессор, он не может быть прерван, пока не истечет его квант времени.
- С прерыванием процессов – если приходит новый процесс, время активности которого меньше, чем оставшееся время активного процесса, - прервать активный процесс. Эта схема известна под названием Shortest-Remaining-Time-First (SRTF).
Нетрудно видеть, что стратегия SJF оптимальна, в том смысле, что она обеспечивает минимальное среднее время ожидания для заданного набора процессов.
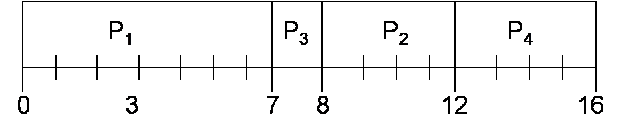
Рассмотрим пример применения стратегии SJF без прерывания процессов. Пусть набор процессов, времен их появления в системе и времен их активности следующие:
Схема их диспетчеризации по стратегии SJF без прерывания процессов приведена на рис. 11.5.
В данном случае среднее время ожидания = (0 + 6 + 3 + 7)/4 = 4.
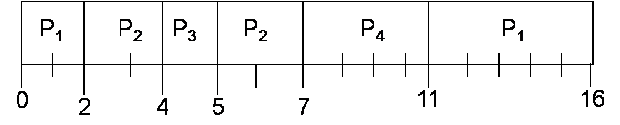
Теперь применим к тем же процессам стратегию SJF с прерыванием и проанализируем, как изменится среднее время ожидания. Результат применения стратегии изображен на рис. 11.6.
В данном случае принцип прерывания процесса в момент поступления в систему более короткого процесса применяется несколько раз:
- в момент 2 прерывается процесс 1 и начинает исполняться более короткий процесс 2;
- в момент 4 прерывается процесс 2 и начинает исполняться более короткий процесс 3.
Из диаграммы видно, что, вследствие применения принципа прерывания процессов, периоды непрерывного выполнения процесса на процессоре могут быть не смежными и перемежаться с периодами выполнения других процессов.
В данном случае среднее время ожидания = (9 + 1 + 0 +2)/4 = 3, т.е. оно, как и следовало предполагать, оказалось меньше, чем без применения принципа прерывания процессов.