| Экстернат |
Целостность сообщения и установление подлинности сообщения
1.1. Целостность сообщения
Системы криптографии, которые мы изучали до сих пор, обеспечивают тайну (секретность) или конфиденциальность, но не целостность. Однако есть случаи, где нам не нужна секретность, но зато необходима целостность (неизменность). Например, Алиса может написать завещание, чтобы распределить свое состояние после ее смерти. Завещание может не быть зашифрованным. После ее смерти любой может посмотреть это завещание. Целостность завещания, однако, должна быть сохранена, ибо Алиса не хочет, чтобы изменяли содержание завещания.
Документ и отпечатки пальцев
Одним из способов сохранить целостность документа мог бы стать способ с помощью отпечатков пальцев. Если Алисе надо быть уверенной, что содержание ее документа не будет изменено, она может поместить отпечаток пальца внизу документа. Ева не может изменить содержание документа или создать ложный документ, потому что она не может подделать отпечаток пальца Алисы. Чтобы гарантировать, что документ не был изменен, отпечаток пальца Алисы на документе можно сравнить с отпечатком пальца Алисы в особом файле. Если они не совпадают, то документ - не от Алисы.
Сообщение и дайджест сообщения
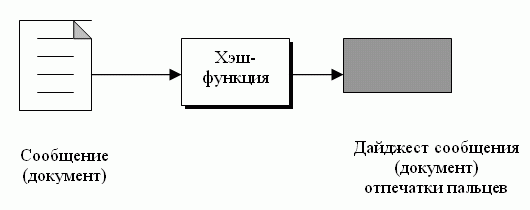
Электронный эквивалент и пары "отпечаток пальца - документ" - это пара сообщение-дайджест. Чтобы сохранить целостность сообщения, оно обрабатывается алгоритмом, называемым криптографической хэш-функцией. Функция создает сжатое изображение сообщения, которое может использоваться подобно отпечатку пальца. рис. 1.1 показывает сообщение, криптографическую хэш-функцию и дайджест сообщения.
Различия
Эти две пары (документ / отпечаток пальца), и ( дайджест сообщения / сообщение) имеют некоторые различия. Документ и отпечаток пальца физически связаны вместе, сообщение и дайджест сообщения могут быть разделены (или быть посланы) отдельно, и, что наиболее важно, дайджест сообщения должен быть защищен от изменения.
Проверка целостности
Чтобы проверить целостность сообщения или документа, мы создаем криптографическую хэш-функцию и сравниваем новый дайджест сообщения с предыдущим. Если они оба - те же самые, мы уверены, что первоначальное сообщение не было изменено. рис. 1.2 иллюстрирует идею.
Криптографические критерии хэш-функции
Криптографическая хэш-функция должна удовлетворять трем критериям (см. рис. 1.3): устойчивости к прообразу, устойчивости ко второму прообразу и устойчивости к коллизиям.
Устойчивость прообраза
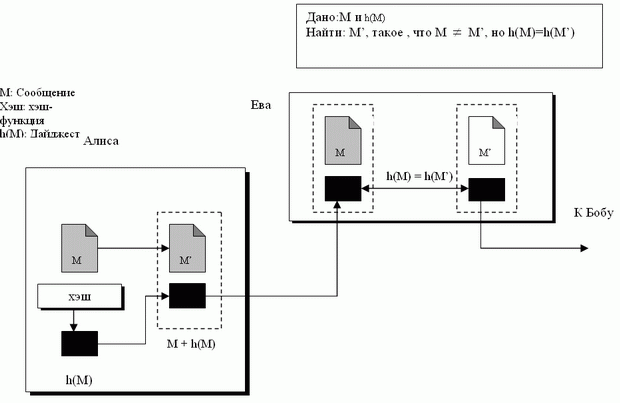
Криптографическая функция должна быть устойчива к прообразу. Если дана хэш-функция h и y = h(M), то для Евы должно быть экстремально трудно найти сообщение, такое, что y = h(M'). рис. 1.4 иллюстрирует эту идею.
Если хэш-функция - неустойчивый прообраз, Ева может перехватить дайджест h(M), создать сообщение M' и затем передать M' Бобу вместо исходного М.
Атака прообраза
Дано: y = h (M) Найти: такое М', что y = h (M').Пример 1.1
Можем ли мы использовать обычный метод сжатия без потерь, такой, например, как zip, в криптографической хэш-функции?
Решение
Не можем. Метод сжатия без потерь создает сжатое сообщение, которое должно быть обратимо. Вы можете обработать сжатое сообщение, чтобы получить первоначальный текст.
Пример 1.2
Можем ли мы использовать функцию контрольной суммы как криптографическую хэш-функцию?
Решение
Не можем. Функция контрольной суммы - не стойкий прообраз. Ева может найти несколько сообщений, контрольная сумма которых соответствует данной.
Устойчивость ко второму прообразу
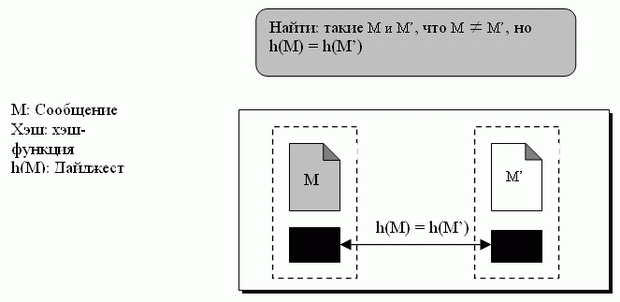
Второй критерий, устойчивость ко второму прообразу, гарантирует, что сообщение не может легко быть подделанным. Ева не может легко создать другое сообщение, которое преобразуется в тот же самый дайджест. Другими словами, учитывая заданное сообщение и его дайджест, невозможно (или, по крайней мере, очень трудно) создать другое сообщение с тем же самым дайджестом. рис. 1.5 иллюстрирует идею.
Ева перехватывает (имеет доступ к) сообщение М и его дайджест h(M). Она создает другое сообщение М.' М., но h (M) = h(M'). Ева передает М.' и h (M') Бобу. Ева подделала сообщение.
Атака второго прообраза
Дана Атака: М и h (M) Найти: такое M' = М, что h (M) = h (M').
Устойчивость к коллизиям
Третий критерий, устойчивость к коллизиям, гарантирует, что Ева не может найти два сообщения, которые приводят к тому же самому дайджесту. Здесь противник может создать два сообщения (из рабочего) и привести к тому же дайджесту. Мы увидим позже, как Ева может извлечь выгоду из этой слабости хэш-функции. Предположим, что в течение одного и того же момента времени созданы два различных завещания, которые могут быть приведены к одному тому же дайджесту. Когда наступает время для выполнения завещания, второе (подделанное) завещание представляется наследникам. Поскольку дайджест соответствует обоим завещаниям, подстановка не обнаружена. рис. 1.6 иллюстрирует идею. Мы увидим позже, что этот тип атаки намного проще начать, чем два предыдущих вида. Другими словами, мы должны твердо убедиться, что хэш-функция устойчива к коллизиям.