| Экстернат |
Квадратичное сравнение
Пример 13.13
Для какого значения n группа 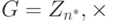 имеет примитивные корни: 17, 20, 38 и 50?
имеет примитивные корни: 17, 20, 38 и 50?
Решение
a.  имеет примитивные корни, потому что 17 — простое число ( pt, где t равно 1 ).
имеет примитивные корни, потому что 17 — простое число ( pt, где t равно 1 ).
b.  не имеет никаких примитивных корней.
не имеет никаких примитивных корней.
c.  имеет первообразные корни, потому что
имеет первообразные корни, потому что 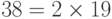 и 19 — простое число.
и 19 — простое число.
d.  имеет первообразные корни, потому что
имеет первообразные корни, потому что 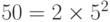 , а 5 — простое число.
, а 5 — простое число.
Если группа имеет примитивный корень, то обычно она имеет несколько таких корней. Число примитивных корней может быть вычислено как —  . Например, число примитивных корней
. Например, число примитивных корней  — это —
— это —  . Обращаем внимание, что нужно сначала проверить, имеет ли группа какой-либо примитивный корень, прежде чем находить число корней.
. Обращаем внимание, что нужно сначала проверить, имеет ли группа какой-либо примитивный корень, прежде чем находить число корней.
 (
(  (n))
(n))
Рассмотрим три вопроса:
1. Если дан элемент a и группа 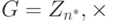 , как можно определить, является ли a примитивным корнем G? Это не такая легкая задача.
, как можно определить, является ли a примитивным корнем G? Это не такая легкая задача.
а. Мы должны найти  , — эта задача по сложности подобна задаче разложения на множители числа n.
, — эта задача по сложности подобна задаче разложения на множители числа n.
б. Мы должны найти 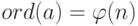 .
.
2. Если дана группа 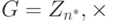 , как найти все примитивные корни
, как найти все примитивные корни 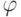 ? Эта задача более трудная, чем первая задача, потому что мы должны повторить вычисления по п.1.б для всей группы.
? Эта задача более трудная, чем первая задача, потому что мы должны повторить вычисления по п.1.б для всей группы.
3. Если дана группа 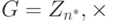 , то как выбирать примитивный корень G? В криптографии мы должны найти, по крайней мере, один примитивный корень в группе. Однако в этом случае значение n выбирается пользователем, и пользователь знает
, то как выбирать примитивный корень G? В криптографии мы должны найти, по крайней мере, один примитивный корень в группе. Однако в этом случае значение n выбирается пользователем, и пользователь знает  . Пользователь пробует последовательно несколько элементов, пока не находит первый из них.
. Пользователь пробует последовательно несколько элементов, пока не находит первый из них.
Циклическая группа. Циклические группы уже обсуждались в лекциях 5-6. Обратите внимание на то, что, если группа 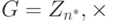 имеет примитивные корни, то они циклически повторяются. Каждый примитивный корень — генератор и может использоваться для создания целого набора. Другими словами, если g — примитивный корень в группе, мы можем генерировать набор Zn* как
имеет примитивные корни, то они циклически повторяются. Каждый примитивный корень — генератор и может использоваться для создания целого набора. Другими словами, если g — примитивный корень в группе, мы можем генерировать набор Zn* как
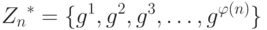
Пример 13.14
Группа  имеет два примитивных корня, потому что
имеет два примитивных корня, потому что  и
и 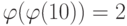 . Можно найти примитивные корни - это 3 и 7. Ниже показано, как можно создать целый набор Z10*, использующий каждый примитивный корень.
. Можно найти примитивные корни - это 3 и 7. Ниже показано, как можно создать целый набор Z10*, использующий каждый примитивный корень.
g = 3 -> g1 mod 10 = 3 g2 mod 10 = 9 g3 mod 10 = 7 g4 mod 10 = 1 g = 7 -> g1 mod 10 = 7 g2 mod 10 = 9 g3 mod 10 = 3 g4 mod 10 = 1
Обратите внимание, что группа 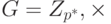 всегда циклическая, потому что p — простое.
всегда циклическая, потому что p — простое.
Группа G = < Zn*, x > является циклической группой, если она имеет примитивные корни. Группа G = < Zp*, x > всегда является циклической.
Идея дискретного логарифма. Группа  имеет несколько интересных свойств.
имеет несколько интересных свойств.
- Её элементы включают все целые числа от 1 до p – 1.
- Она всегда имеет примитивные корни.
- Она всегда является циклической. Элементы могут быть созданы с использованием gx, где x — целое число от 1 до
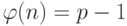 .
. - Примитивные корни можно представлять себе как основание логарифма. Если группа имеет k примитивных корней, то вычисления могут быть сделаны для k различных оснований. Данный x = logg y для любого элемента y в данном множестве, но есть другой элемент x, который является логарифмом y по основанию g. Этот тип логарифма называют дискретным логарифмом. Дискретный логарифм в литературе определяется несколькими различными символами, но мы будем использовать обозначение Lg, чтобы показать, что основание — g (сравнение по модулю).
Решение модульного логарифма с использованием дискретных логарифмов
Теперь рассмотрим, как решаются задачи типа y = ax (mod n), т. е. дано y, а мы должны найти x.
Табулирование дискретных логарифмов. Один из способов решения вышеупомянутой проблемы — использовать таблицу для каждого Zp* и различных оснований. Этот тип таблицы может быть предварительно рассчитан и сохранен. Например, таблица 13.4 показывает значения дискретного логарифма для Z7*. Мы знаем, что мы имеем два примитивных корня или основания в данном множестве.
| y | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| x = L3y | 6 | 2 | 1 | 4 | 5 | 3 |
| x = L5y | 6 | 4 | 5 | 2 | 1 | 3 |
Составив таблицы для других дискретных логарифмов для всех групп и всех возможных оснований, мы можем решить любую дискретную логарифмическую проблему. Этот подход подобен изучаемым в прошлом традиционным логарифмам. До появления калькуляторов и компьютеров таблицы использовались, чтобы вычислять логарифмы по основанию 10.
Пример 13.15
Найдите x в каждом из следующих случаев:
a. 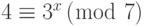
b. 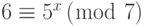
Решение
Мы можем легко использовать таблицу 13.4 дискретного логарифма.
a. 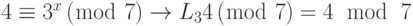
b. 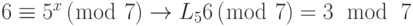
Использование свойств дискретных логарифмов. Чтобы показать, что дискретные логарифмы ведут себя точно так же, как традиционные логарифмы, в таблице 13.5 приводится несколько свойств обоих типов логарифмов. Обратите внимание, что основание модуля —  вместо n.
вместо n.
Использование алгоритмов, основанных на дискретных логарифмах. Таблицы и свойства дискретных логарифмов не могут быть использованы для решения уравнения y = a x (mod n), когда n является очень большим. Для решения этой проблемы были разработаны несколько алгоритмов, в которых используется основная идея дискретных логарифмов. Хотя все эти алгоритмы более эффективны, чем алгоритмы полного перебора, которые мы упоминали в начале этого раздела, но ни один из них не имеет полиномиальную сложность. Большинство этих алгоритмов имеет такой же уровень сложности, как проблема разложения на множители.

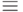 0(mod
0(mod