| Экстернат |
Введение в основы современных шифров с симметричным ключом
Компоненты современного блочного шифра
Современные блочные шифры обычно являются ключевыми шифрами подстановки, в которых ключ позволяет только частичные отображения возможных входов информации в возможные выходы. Однако эти шифры обычно не проектируются как единый модуль. Чтобы обеспечивать требуемые свойства современного блочного шифра, такие как рассеяние и перемешивание информации (обсуждается кратко), этот шифр формируется как комбинация модулей транспозиции (называемых P -блоками), модулей подстановки (называемых S -блоками) и некоторыми другими модулями (обсуждается кратко).
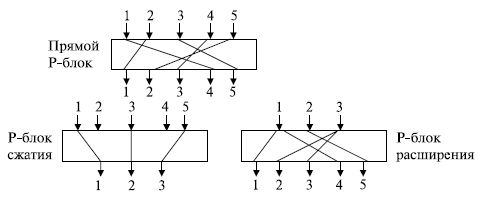
P -блок (блок перестановки) подобен традиционному шифру транспозиции символов. Он перемещает биты. В современных блочных шифрах мы можем найти три типа P -блоков: прямые P -блоки, P -блоки расширения и P -блоки сжатия, что и показано на рис. 7.4.
Рисунок 7.4 показывает прямой P -блок  , P -блок сжатия
, P -блок сжатия  и P -блок расширения
и P -блок расширения  . Рассмотрим каждый из них более подробно.
. Рассмотрим каждый из них более подробно.
Прямые P-блоки.Прямой P -блок с n входами и n выходами – это перестановка с n! возможными отображениями.
Пример 7.5
Рисунок 7.5 показывает все 6 возможных отображений P -блока  .
.
Хотя P -блок может использовать ключ, чтобы определить одно из n! отображений, обычно P -блоки – без применения ключа, то есть отображение задано заранее. Если P -блок задан заранее и замонтирован в аппаратных средствах или если он реализован в программном обеспечении, таблицы перестановок задают правило отображения. Во втором случае входы в таблице указывают в позиции, в которых указаны позиции выходов. Таблица 7.1 дает пример таблицы перестановок, когда n равно 64.
| 58 | 50 | 42 | 34 | 26 | 18 | 10 | 02 | 60 | 52 | 44 | 36 | 28 | 20 | 12 | 04 |
| 62 | 54 | 46 | 38 | 30 | 22 | 14 | 06 | 64 | 56 | 48 | 40 | 32 | 24 | 16 | 08 |
| 57 | 49 | 41 | 33 | 25 | 17 | 09 | 01 | 59 | 51 | 43 | 35 | 27 | 19 | 11 | 03 |
| 61 | 53 | 45 | 37 | 29 | 21 | 13 | 05 | 63 | 55 | 47 | 39 | 31 | 23 | 15 | 07 |
Таблица 7.1 имеет 64 табличных входа, которые фиксируют соответствие 64 информационным входам. Позиция (индекс) входа соответствует выходу. Например, первый табличный вход содержит номер 58. Это означает, что первый выход будет соответствовать 58 -му входу. Поскольку последний табличный вход — 7, это означает, что, 64 -й выход будет соответствовать седьмому информационному входу, и так далее.
Пример 7.6
Составьте таблицу перестановки для прямого P -блока 8 x 8, которая перемещает два средних бита (биты 4 и 5 ) во входном слове к двум крайним битам (биты 1 и 8 ) выходного слова. Относительные позиции других битов не изменяются.
Решение
Нам надо создать прямой P -блок с таблицей [4 1 2 3 6 7 8 5]. Относительные позиции бит 1, 2, 3, 6, 7 и 8 не меняются, но первый информационный выход связан с четвертым информационным входом, восьмой информационный выход — с пятым информационным входом.
P-блоки сжатия. P -блок сжатия – это P -блок с n входами и m выходами, где m <n. Некоторые из информационных входов блокированы и не связаны с выходом (см. рисунок 7.4). P -блоки сжатия, используемые в современных блочных шифрах, обычно являются безключевыми с таблицей перестановки, которая указывает правила перестановки бит. Нам надо учитывать, что таблица перестановок для P -блока сжатия имеет m табличных входов, но в содержании каждого табличного входа – от 1 до n, и некоторые из них могут отсутствовать (те информационные входы, которые блокированы). Таблица 7.2 показывает пример таблицы перестановки для P -блока сжатия  . Обратите внимание, что входы 7, 8, 9, 16, 23, 24 и 25 блокированы.
. Обратите внимание, что входы 7, 8, 9, 16, 23, 24 и 25 блокированы.
| 01 | 02 | 03 | 21 | 22 | 26 | 27 | 28 | 29 | 13 | 14 | 17 |
| 18 | 19 | 20 | 04 | 05 | 06 | 10 | 11 | 12 | 30 | 31 | 32 |
P -блоки сжатия используются, когда мы должны переставить биты и в то же время уменьшить число битов для следующей ступени.
P-блок расширения — P -блок с n входами и m выходами, где m> n. Некоторые из входов связаны больше чем с одним выходом (см. рис. 7.4). P -блоки расширения, используемые в современных блочных шифрах, обычно без ключа. Правила перестановки бит указываются в таблице. Таблица перестановки для P -блока расширения имеет m табличных входов, но m – n входов (те входы, которые связаны больше чем с одним информационным выходом). Таблица 7.3 показывает пример таблицы перестановки для P -блока расширения 12 16. Обратите внимание, что каждый из 1, 3, 9 и 12 соединен с двумя выходами.
P -блоки расширения используются, когда мы должны переставить биты и то же время увеличить число битов для следующего каскада шифрования.
Обратимость.Прямой P -блок является обратимым. Это означает, что мы можем использовать прямой P -битовый шифр и дешифровать его. Таблицы перестановки, однако, должны быть обратимыми по отношению друг к другу. В лекциях 5-6 мы видели, как можно получить обратную таблицу перестановки.
Пример 7.7
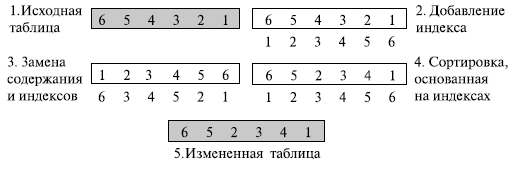
Рисунок 7.6 показывает, как изменить таблицу перестановки в случае одномерной таблицы.
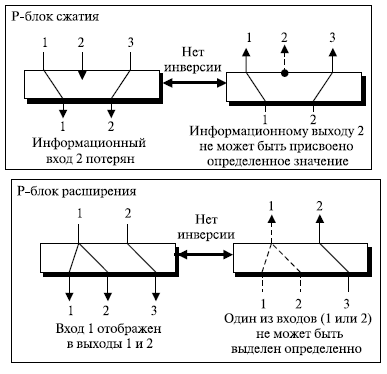
P -блоки сжатия и расширения необратимы. В P -блоках сжатия вход может быть отброшен в процессе шифрования; алгоритм дешифрования не имеет ключа, чтобы восстановить отброшенный бит. В P -блоке расширения вход в процессе шифрования может быть отображен более чем в один выход; алгоритм дешифрования не имеет ключа и не определяет тем самым, какие из нескольких входов отображены в данном выходе. Рисунок 7.7 демонстрирует оба случая.
Рисунок 7.7 также показывает, что P -блок сжатия не является обратным шифром P -блока расширения и наоборот. Это означает, что если мы используем P -блок сжатия для шифрования, мы не сможем использовать P -блок расширения для дешифрования и наоборот. Однако, как будет показано позже в этой лекции, есть шифры, которые применяют P -блоки сжатия или расширения для шифрования; но их эффективность хуже, чем у некоторых других способов.
S-блоки
S-блок (блок подстановки) можно представить себе как миниатюрный шифр подстановки. Этот блок может иметь различное число входов и выходов. Другими словами, вход к S -блоку может быть n -битовым словом, а выход может быть m разрядным словом, где m и n — не обязательно одинаковые числа. Хотя S -блок может быть ключевым или без ключа, современные блочные шифры обычно используют S -блоки без ключей, где отображение от информационных входов к информационным выходам заранее определено.
Линейный и нелинейный S-блоки. В S -блоке с n входами и m выходами мы обозначим входы x0, x1,…., xn и выходы y1 ,..., ym. Соотношения между входами и выходами могут быть представлены как система уравнений
y1 = f1 (x1,x2,…,xn)
y2 = f2 (x1,x2,…,xn)
….
ym = fm (x1,x2,…,xn)
В линейном S-блоке вышеупомянутые соотношения могут быть выражены как

В нелинейном S-блоке мы не можем всегда задать для каждого выхода указанные выше соотношения.
Пример 7.8
В S -блоке с тремя входами и двумя выходами мы имеем
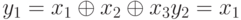
S -блок линеен, потому что a1,1 = a1,2 = a1,3 = a2,1=1 и a2 ,2 = a2 ,3 = 0. Эти соотношения могут быть представлены матрицами, как показано ниже:
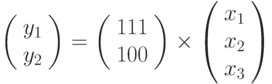
Пример 7.9
В S -блоке с тремя входами и двумя выходами мы имеем
y1 = (x1)3 + x2 y2 = (x1) + x1x2 + x3
где умножение и сложение проводится в GF(2). S -блок нелинеен, потому что нет линейных соотношений между входами и выходами.
Пример 7.10
Следующая таблица определяет отношения между входами/выходами для S -блока размера  . Крайний левый бит входа определяет строку; два самых правых бита входа определяют столбец. Два бита выхода – это значение на пересечении секции выбранной строки и столбца.
. Крайний левый бит входа определяет строку; два самых правых бита входа определяют столбец. Два бита выхода – это значение на пересечении секции выбранной строки и столбца.
Обратимость. S -блоки — шифры подстановки, в которых отношения между входом и выходом определены таблицей или математическим соотношением. S -блок может быть или может не быть обратимым. В обратимом S -блоке число входных битов должно быть равным числу бит выхода.
Пример 7.11
Рисунок 7.8 показывает пример обратимого S -блока. Одна из таблиц используется в алгоритме шифрования; другая таблица — в алгоритме дешифрования. В каждой таблице крайний левый бит входа определяет строку; следующие два бита определяют столбец. Выход — это значение на пересечении строки и столбца.
Например, если вход к левому блоку — 001, выход — 101. Вход 101 в правой таблице дает выход 001. Это показывает, что эти две таблицы позволяют получить обратный результат по отношению друг к другу.