| Экстернат |
Алгоритмы сжатия данных
3.1. Алгоритм Зива-Лемпеля
В 1977 году Абрахам Лемпель и Якоб Зив предложили алгоритм сжатия данных, названный позднее LZ77. Этот алгоритм используется в программах архивирования текстов compress, lha, pkzip и arj. Модификация алгоритма LZ78 применяется для сжатия двоичных данных. Эти модификации алгоритма защищены патентами США. Алгоритм предполагает кодирование последовательности бит путем разбивки ее на фразы с последующим кодированием этих фраз. Суть алгоритма заключается в следующем.
Если в тексте встретится повторение строк символов, то повторные строки заменяются ссылками (указателями) на исходную строку. Ссылка имеет формат <префикс, расстояние, длина>. Префикс в этом случае равен 1. Поле расстояние идентифицирует слово в словаре строк. Если строки в словаре нет, генерируется код символ вида <префикс, символ>, где поле префикс = 0, а поле символ соответствует текущему символу исходного текста. Отсюда видно, что префикс служит для разделения кодов указателя от кодов символ. Введение кодов <символ> позволяет оптимизировать словарь и поднять эффективность сжатия. Главная алгоритмическая проблема здесь заключается в оптимальном выборе строк, так как это предполагает значительный объем переборов.
Рассмотрим пример с исходной последовательностью U = 0010001101 (без надежды получить реальное сжатие для столь ограниченного объема исходного материала). Введем обозначения:
- P[n] — фраза с номером n ;
- C — результат сжатия.
Разложение исходной последовательности бит на фразы представлено в таблице 3.1.
P[0] — пустая строка. Символом "." (точка) обозначается операция объединения (конкатенации).
| N фразы | Значение | Формула | Исходная последовательность U |
|---|---|---|---|
| 0 | P[0] | 0010001101 | |
| 1 | 0 | P[1] = P[0].0 | 0.010001101 |
| 2 | 01 | P[2] = P[1].1 | 0.01.0001101 |
| 3 | 010 | P[3] = P[1].0 | 0.01.00.01101 |
| 4 | 00 | P[4] = P[2].1 | 0.01.00.011.01 |
| 5 | 011 | P[5] = P[1].1 | 0.01.00.011.01 |
Формируем пары строк, каждая из которых имеет вид (A.B). Каждая пара образует новую фразу и содержит идентификатор предыдущей фразы и бит, присоединяемый к этой фразе. Объединение всех этих пар представляет окончательный результат сжатия С. P[1] = P[0].0 дает (00.0), P[2] = P[1].0 дает (01.0) и т.д. Схема преобразования отражена в таблице ниже.
| Формулы | P[1] = P[0].0 | P[2] = P[1].1 | P[3] = P[1].0 | P[4] = P[2].1 | P[5] = P[1].1 |
|---|---|---|---|---|---|
| Пары | 00.0 = 000 | 01.1 = 011 | 01.0 = 010 | 10.1 = 101 | 01.1 = 011 |
| С | 000.011.010.101.011 = 000011010101011 | ||||
Все формулы, содержащие P[0], вовсе не дают сжатия. Очевидно, что С длиннее U, но это получается для короткой исходной последовательности. В случае материала большего объема будет получено реальное сжатие исходной последовательности. Приведенный пример позволяет понять, что не всякая операция архивации приводит к реальному сокращению объема данных.
3.2. Статический алгоритм Хаффмана
Статический алгоритм Хафмана можно считать классическим (см. также Р. Галлагер. Теория информации и надежная связь. "Советское радио", Москва, 1974). Определение "статический" в данном случае относится к используемым словарям. См. также http://www.ics.ics.uci.edu/~dan/pubs/DataCompression.html) (Debra A. Lelewer и Daniel S. hirschberg). Алгоритм Хаффмана предполагает, что вероятности появления в исходном массиве разных кодовых последовательностей (символов) принципиально неравны.
Пусть сообщения 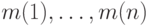 имеют вероятности
имеют вероятности 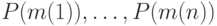 и пусть для определенности они упорядочены так, что
и пусть для определенности они упорядочены так, что 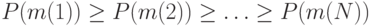 . Пусть
. Пусть  - совокупность двоичных кодов, и пусть
- совокупность двоичных кодов, и пусть 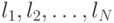 — длины этих кодов. Задачей алгоритма является установление соответствия между
— длины этих кодов. Задачей алгоритма является установление соответствия между 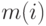 и
и  . Можно показать, что для любого ансамбля сообщений с полным числом более 2 существует двоичный код, в котором два наименее вероятных кода
. Можно показать, что для любого ансамбля сообщений с полным числом более 2 существует двоичный код, в котором два наименее вероятных кода  и
и 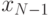 имеют одну и ту же длину и отличаются лишь последним символом:
имеют одну и ту же длину и отличаются лишь последним символом:  имеет последний бит 1, а
имеет последний бит 1, а 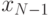 - 0.
Редуцированный ансамбль будет иметь свои два наименее вероятные сообщения сгруппированными вместе. После этого можно получить новый редуцированный ансамбль, и так далее. Процедура может быть продолжена до тех пор, пока в очередном ансамбле не останется только два сообщения. Процедура реализации алгоритма сводится к следующему (см.
рис.
3.1). Сначала группируются два наименее вероятных сообщения, предпоследнему сообщению ставится в соответствие код с младшим битом, равным нулю, а последнему – код с единичным младшим битом (на рисунке
- 0.
Редуцированный ансамбль будет иметь свои два наименее вероятные сообщения сгруппированными вместе. После этого можно получить новый редуцированный ансамбль, и так далее. Процедура может быть продолжена до тех пор, пока в очередном ансамбле не останется только два сообщения. Процедура реализации алгоритма сводится к следующему (см.
рис.
3.1). Сначала группируются два наименее вероятных сообщения, предпоследнему сообщению ставится в соответствие код с младшим битом, равным нулю, а последнему – код с единичным младшим битом (на рисунке 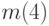 и
и 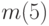 ). Вероятности этих двух сообщений складываются, после чего ищутся два наименее вероятные сообщения во вновь полученном ансамбле (
). Вероятности этих двух сообщений складываются, после чего ищутся два наименее вероятные сообщения во вновь полученном ансамбле ( 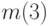 и
и 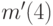 ;
;  ).
).
На следующем шаге наименее вероятными сообщениями окажутся  и
и 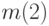 . Кодовые слова на полученном дереве считываются справа налево. Алгоритм выдает оптимальный код (минимальная избыточность).
. Кодовые слова на полученном дереве считываются справа налево. Алгоритм выдает оптимальный код (минимальная избыточность).
При использовании кодирования по схеме Хаффмана надо вместе с закодированным текстом передать соответствующий алфавит. При передаче больших фрагментов избыточность, сопряженная с этим, не может быть значительной.
Возможно применение стандартных алфавитов (кодовых таблиц) для пересылки английских, русских, французских и т.п. текстов, программных текстов на С++, Паскале и т.д. Кодирование при этом не будет оптимальным, но исключается статистическая обработка пересылаемых фрагментов и отпадает необходимость пересылки кодовых таблиц (алфавитов). Следует заметить, что и в случае алгоритма Хаффмана эффективность сжатия зависит от характера сжимаемого материала. Например, при попытке сжать уже архивированный файл с большой вероятностью можно получить файл большего размера.

