| Экстернат |
Цифровая подпись
3.6. Варианты и приложения
В этой секции кратко обсуждаются варианты и приложения для цифровых подписей.
Варианты
Ниже проводится краткое обсуждение некоторых вариантов и дополнений к главному понятию цифровых подписей. Для более четкого понимания читатель может посмотреть специальную литературу.
Подпись с указанием времени
Иногда подписанный документ должен иметь указание времени, чтобы препятствовать действиям противника. Это названо схемой цифровой подписи с указанием времени.
Например, Алиса подписывает запрос своему банку (условно Бобу), выдать некоторую сумму денег Еве. Документ может быть перехвачен Евой, если на этом документе нет никакого указания времени.
Включение фактической даты и времени на документах может создать проблемы - несинхронизированные часы, отсутствие универсального времени. Одно решение состоит в том, чтобы использовать nonce (number only once - Nonce) - одноразовое случайное число, которое может быть использовано только однажды. Когда приемник получает документ с nonce, он составляет примечание, что число было использовано передатчиком и не может использоваться снова. Другими словами, новый nonce - "настоящее время"; использованный nonce определяет "прошлое время".
Слепые подписи
Иногда мы имеем документ, который хотим подписать, не раскрывая содержание документа подписывающему лицу. Например, ученый хочет сообщить Бобу, что он, возможно, открыл очень важную теорию, которую необходимо подписать у обычного нотариуса. Он просит Алису передать это, не разрешая ей узнать содержание теории. Для этой цели Дэвид Чом (David Caum) разработал некоторые патентованные слепые схемы цифровой подписи. Главная идея состоит в следующем.
- Боб создает сообщение и маскирует (затемняет) его. Боб передает маскированное сообщение Алисе.
- Алиса подписывает замаскированное сообщение и возвращает подпись на замаскированном сообщении.
- Боб снимает немаскированную подпись, чтобы получить подпись на первоначальном сообщении.
Слепая подпись, основанная на схеме RSА. Опишем кратко слепую схему цифровой подписи, разработанную Дэвидом Чомом. Маскировка может быть сделана с использованием варианта схемы RSA. Боб выбирает случайное число, b, и вычисляет слепое сообщение B = М. x be mod n, в котором e является открытым ключом Алисы и n - определенным модулем в схеме цифровой подписи RSА. Обратите внимание, что b иногда называется "маскирующим коэффициентом", который Боб передает Алисе.
Алиса подписывает маскированное сообщение, используя алгоритм подписания, определенный в RSA. Цифровая подпись - Sblind = Bd mod n, где d является секретным ключом Алисы. Обратите внимание, что Sb - подпись на слепой (маскированной) версии сообщения.
Боб просто использует мультипликативную инверсию его случайного числа b, чтобы отделить слепое сообщение от подписи. Подпись - S = Sb b-1 mod n. Мы можем доказать, что S - подпись на первоначальном сообщении, как это определено в схеме цифровой подписи RSA:
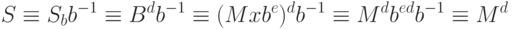
S - подпись, если Боб передал первоначальное сообщение, которое будет подписано Алисой.
Предотвращение мошенничества. При слепой подписи появляется опасность, что Боб, может дать Алисе подписать слепое сообщение, которое может навредить ей. Например, сообщение Боба могло быть документом, утверждающим, что Алиса передаст Бобу все свое имущество после ее смерти. Есть по крайней мере три способа предотвратить такой ущерб.
- Администрация может издать юридический акт, что Алиса не ответственна за подпись любого слепого сообщения, которое нарушает ее интересы.
- Алиса может запросить документ от Боба, что сообщение, которое она подпишет, не наносит ей ущерба.
- Алиса могла бы требовать, чтобы Боб доказал свою честность прежде, чем она подпишет ему слепое сообщение
Бесспорные схемы цифровой подписи - изящное изобретение Чома и Ван Антверпена (van Antwerpen). Бесспорная схема цифровой подписи имеет три компонента: алгоритм подписания, протокол проверки и протокол отрицания. Алгоритм подписания позволяет Алисе подписывать сообщение. Протокол проверки использует механизм вызова-ответа (рассмотренный в "Установление подлинности объекта" ), с его помощью Алиса может подтвердить свою подпись. Это предотвращает копирование и распределение подписанного сообщения без одобрения Алисы. Протокол отрицания помогает Алисе отрицать фальшивую подпись. Чтобы потом иметь возможность доказать, что подпись - подделка, Алиса должна принять участие в составлении протокола отрицания.
Приложения
В дальнейшем в этой книге обсуждаются несколько приложений криптографии для сетевой безопасности. Большинство этих приложений непосредственно или косвенно требует использования открытых ключей. Чтобы использовать открытый ключ, человек должен доказать, что он законно владеет этим ключом. По этой причине была разработана идея сертификации и свидетельств сертификации (CA) (См. "Установление подлинности объекта" и "Управление ключами" ). Свидетельства (CA), чтобы быть признанными, должны быть подписаны. Цифровые подписи используются, чтобы обеспечить такое доказательство. Когда Алиса должна применить открытый ключ Боба, она пользуется свидетельством. Сертифицированные CA используют общедоступный ключ с секретным ключом и проверяемой подписью Алисы. Само свидетельство содержит общедоступный ключ Боба.
Сегодняшние протоколы, которое используют услуги CA, - это IPSec ( "Безопасность на сетевом уровне: IP SEC" ), SSL/TLS ( "Безопасность на транспортном уровне: SSL и TLS" ) и S/MIME ( "Безопасность на прикладном уровне: PGP и S/MIME" ). Протокол PGP поддерживает свидетельства, но они могут быть заменены соглашениями между людьми в сообществе.
3.7. Рекомендованная литература
Для более детального изучения положений, обсужденных в этой лекции, мы рекомендуем нижеследующие книги и сайты. Пункты, указанные в скобках, показаны в списке ссылок в конце книги.
Книги
[Sti06], [TW06] и [PHS03] подробно рассматривают цифровые подписи.
Сайты
Нижеследующие сайты дают больше информации о темах, обсужденных в этой лекции.
- http://www.itl.nist.gcv/npspubs/fip 186.htm
- csrc.nist.gov/publiCti ions/tips/tips 186-2/fipsl 86-2-changel
- http://en.wikipedia.org /wiki/ElGamal_signature_scheme
- csrc.nist.gov/cryptvd/dss/ECDSAVS.pdf
- http://en.wikipedia.('og/wiki/ElGamal_signature_scheme
- http://en.wikipedia.org/wiki/Digital_signature
3.8. Итоги
- Схема цифровой подписи может обеспечить те же самые услуги, что и обычная подпись. Обычная подпись - это часть документа; цифровая подпись - отдельный объект. Чтобы проверять обычную подпись, получатель сравнивает подпись с подписью в архиве; чтобы проверять цифровую подпись, получатель на основе документа проводит процесс подтверждения подписи. Между документом и обычной подписью отношение "один к многим"; Между цифровой подписью и документом отношение "один к одному".
- Цифровые подписи обеспечивают установление подлинности сообщения, а также целостность сообщения, если дайджест сообщения подписан непосредственно вместо сообщения, и исключение отказа от сообщения, если используется третье лицо, которому доверяют.
- Цифровая подпись не может обеспечить конфиденциальность сообщения. Если необходима конфиденциальность, кроме схемы цифровой подписи должна быть применена криптографическая система.
- Цифровая подпись нуждается в асимметрично-ключевой системе. В криптографической системе мы используем секретные и открытые ключи приемника; для цифровых подписей мы используем секретные и открытые ключи передатчика.
- Схема цифровой подписи RSA использует криптографическую систему RSA, но роли секретных и открытых ключей изменяются. Схема цифровой подписи Эль-Гамаля применяет криптосистему Эль-Гамаля (с некоторыми незначительными изменениями), но роли секретных и открытых ключей здесь иные. Схема цифровой подписи Шнорра - модификация схемы Эль-Гамаля, в которой размер подписи может быть меньшим. Стандарт Цифровой подписи (DSS) использует алгоритм цифровой подписи (DSA), который базируется на схеме Эль-Гамаля с некоторыми идеями из схемы Шнорра.
- Схема цифровой подписи с указанием времени разработана для предотвращения повторного использования подписей. Слепые схемы цифровой подписи позволяют Бобу просить Алису подписать документ, не показывая его содержание. Бесспорная схема цифровой подписи нуждается в алгоритме подписания, протоколе проверки и протоколе отрицания для предотвращения копирования и распределения подписанного сообщения без одобрения подписывающего лица.
- Главное приложение цифровых подписей - это Центры сертификации (CA).
3.9. Набор для практики
Обзорные вопросы
- Сравните и противопоставьте обычную подпись и цифровую подпись.
- Перечислите службы безопасности, которые требуют обеспечения цифровой подписью.
- Сравните и противопоставьте атаки цифровых подписей с атаками криптографических систем.
- Сравните и противопоставьте экзистенциальную и селективную подделки.
- Дайте определение схеме цифровой подписи RSA и сравните ее с криптографической системой RSA.
- Дайте определение схеме Эль-Гамаля и сравните ее со схемой RSA.
- Дайте определение схеме Шнорра и сравните ее со схемой Эль-Гамаля.
- Дайте определение схеме стандарта цифровой подписи (DSS) и сравните ее со схемами Эль-Гамаля и Шнорра.
- Дайте определение схеме цифровой подписи эллиптической кривой и сравните ее с криптосистемой на основе метода эллиптических кривых.
- Рассмотрите три варианта цифровых подписей, приведенных в этой лекции, и кратко сформулируйте цель каждой.
Упражнения
- Используя схему RSA, при p = 809, q = 751, и d = 23, вычислите общедоступный ключ e.
Затем
- Подпишите и проверьте сообщение M1 = 100. Получите подпись S1.
- Подпишите и проверьте сообщение с М2 = 50. Получите подпись S2.
- Покажите, что если М = M1 x М2 = 5000, то S = S1 x S2.
- Используя схему Эль-Гамаля при p = 881 и d = 700, найдите значения e1 и e2. Выберите r = 17. Найдите значение S1 и S2, если М = 400.
- Используя схему Шнорра, при q = 83, p = 997 и d = 23, найдите значения для e1 и e2. Выберите r = 11. Если М
= 400 и h (400) = 100, найдите значение S1., S2 и V. Равно ли
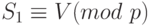 ?
? - Используя схему DSS, при q = 59, p = 709 и d = 14, найдите значения для e1 и e2. Выберите r = 13. Найдите значение S1 и S2, если h (M) = 100. Проверьте подпись.
- Сделайте следующее:
- NIST-спецификация требует для DSS следующее: если значение S2 = 0, то две подписи должны быть повторно вычислены, используя новый r. Какова причина этого?
- Что случится, если Ева найдет значение r, используемое подписывающим лицом? Возможно ли это в принципе? Объясните ваш ответ отдельно для схем Эль-Гамаля-Шнорра, DSS.
- Что случится, если Алиса подпишет два сообщения, используя одно и то же значение n? Объясните ваш ответ отдельно для каждого протокола: Эль-Гамаля, Шнорра или DSS.
- Покажите пример уязвимости схемы RSA к селективной подделке, когда значения p и q являются маленькими. Используйте p = 19 и q = 3.
- Покажите пример уязвимости схемы Эль-Гамаля к селективной подделке, когда значение p мало. Используйте p = 19.
- Покажите пример уязвимости схемы Шнорра к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
- Покажите пример уязвимости DSS к селективной подделке, когда значения p и q являются маленькими. Используйте p =29 и q = 7.
- В схеме Эль-Гамаля, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
- В схеме Шнорра, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
- В DSS-схеме, если Ева может найти значение r, может ли она подделать сообщение? Объясните.
- Предположим, что значения p, q, e1 и r в схеме Шнорра - те же самые, что и соответствующие значения в DSS-схеме. Сравните значения S1 и S2 в схеме Шнорра с соответствующими значениями в DSS-схеме.
- Объясните, почему в схеме Эль-Гамаля вычисление S2 делается по модулю p, а вычисление S2 делается по модулю p - 1.
- Объясните, почему в схеме Шнорра вычисление S1 делается по модулю p, а вычисление S2 делается по модулю q.
- Объясните, почему в схеме DSS вычисление S1 делается по модулю p и модулю q, а вычисление S2 делается только по модулю q.
- В схеме Шнорра докажите правильность процесса проверки.
- В DSS-схеме докажите правильность процесса проверки.
- В схеме цифровой подписи эллиптической кривой докажите правильность процесса проверки.
- Напишите два алгоритма для схемы RSА: один для процесса подписания и один для процесса проверки.
- Напишите два алгоритма для схемы Эль-Гамаля: один для процесса подписания и один для процесса проверки.
- Напишите два алгоритма для схемы Шнорра: один для процесса подписания и один для процесса проверки.
- Напишите два алгоритма для DSS-схемы: один для процесса подписания и один для процесса проверки.
- Напишите два алгоритма для схемы эллиптической кривой: один для процесса подписания и один для процесса проверки.
