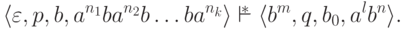| Помогите решить задание лекции 3 курс Математическая теория формальных языков |
Алгоритмические проблемы
Определение 14.1.12.
Пусть f - частичная функция из  в
в  .
Детерминированная машина Тьюринга
.
Детерминированная машина Тьюринга
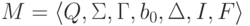
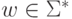 1) если f(w)
не определено,
то не существует таких
1) если f(w)
не определено,
то не существует таких  ,
,  ,
, 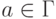 ,
, 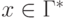 ,
, 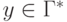 ,
что
,
что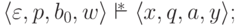
 ,
,  ,
,  и
и 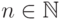 выполнено условие
выполнено условие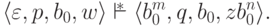
Определение 14.1.13.
Частичная функция из  в
в  называется вычислимой,
если существует детерминированная машина Тьюринга,
вычисляющая эту функцию.
называется вычислимой,
если существует детерминированная машина Тьюринга,
вычисляющая эту функцию.
Пример 14.1.14. Машина Тьюринга из примера 14.1.9 вычисляет следующую частичную функцию:

Пример 14.1.15. Рассмотрим детерминированную машину Тьюринга
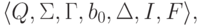
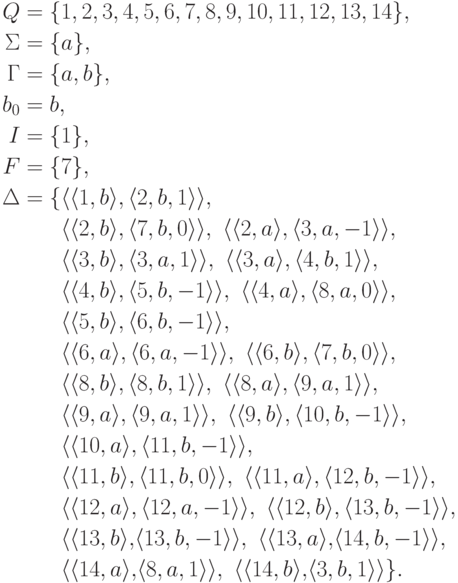
![\objectwidth={5mm} \objectheight={5mm} \let\objectstyle=\scriptstyle
\xymatrix {
%
& *=[o][F=]{7}
& *=[o][F-]{6}
\rloop{0,-1} ^{a:a\dl}
\ar "1,2" _{b:b\dn}
& *=[o][F-]{5}
\ar "1,3" _{b:b\dl}
&
&
\\
%
& *=[o][F-]{1}
\ar @`{+/l16mm/} [] ^{}
\ar "2,3" ^{b:b\dr}
& *=[o][F-]{2}
\ar "1,2" ^*!/u1.5mm/{b:b\dn}
\ar "3,2" ^*!/u2mm/{a:a\dl}
&
&
&
\\
%
& *=[o][F-]{3}
\rloop{0,1} ^{b:a\dr}
\ar "3,4" ^{a:b\dr}
&
& *=[o][F-]{4}
\ar "1,4" _{b:b\dl}
\ar "3,5" ^{a:a\dn}
& *=[o][F-]{8}
\rloop{0,1} ^{b:b\dr}
\ar "3,6" ^{a:a\dr}
& *=[o][F-]{9}
\rloop{0,1} ^{a:a\dr}
\ar "4,5" ^{b:b\dl}
\\
*=[o][F-]{14}
\ar "3,5" <-0.2mm> ^-(.3){a:a\dr}
\ar "3,2" ^{b:b\dr}
& *=[o][F-]{13}
\rloop{0,-1} ^{b:b\dl}
\ar "4,1" ^{a:b\dl}
& *=[o][F-]{12}
\rloop{0,-1} ^{a:a\dl}
\ar "4,2" ^{b:b\dl}
& *=[o][F-]{11}
\rloop{0,-1} ^{b:b\dn}
\ar "4,3" ^{a:b\dl}
& *=[o][F-]{10}
\ar "4,4" ^{a:b\dl}
&
}](/sites/default/files/tex_cache/d83a9b970d547776fa560a10d1a6e7e6.png)
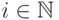 ,
, 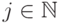 и
и 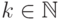 выполняется следующее:
выполняется следующее: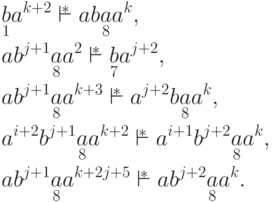
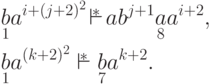

Замечание 14.1.16. Тезисом Черча-Тьюринга
(а иногда просто тезисом Черча )
называется следующее неформальное утверждение:
для каждой вычислимой в интуитивном смысле
частичной функции из  в
в  существует машина Тьюринга,
которая эту функцию вычисляет.
существует машина Тьюринга,
которая эту функцию вычисляет.
Упражнение 14.1.17. Найти детерминированную машину Тьюринга с входным алфавитом {a}, вычисляющую функцию f, заданную соотношением
f(an) = an+1.
Упражнение 14.1.18. Найти детерминированную машину Тьюринга с входным алфавитом {a}, вычисляющую функцию f, заданную соотношением
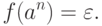
Определение 14.1.19.
Зафиксируем два различных символа a и b
и положим  .
Пусть k -
положительное целое число
и f -
частичная функция из
.
Пусть k -
положительное целое число
и f -
частичная функция из  в
в 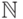 .
Детерминированная машина Тьюринга
.
Детерминированная машина Тьюринга
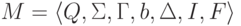
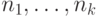 выполняются следующие условия:
выполняются следующие условия:1) если  не определено,
то не существует таких
не определено,
то не существует таких  ,
,  ,
, 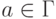 ,
, 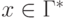 ,
, 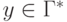 ,
что
,
что
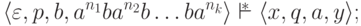
2) если  ,
то
для некоторых
,
то
для некоторых  ,
,  ,
,  и
и 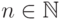 выполнено условие
выполнено условие