| ВКР |
Примеры задач по эконометрике
В настоящем приложении приведены примеры типовых задач, которые решаются на занятиях по эконометрике на факультете "Инженерный бизнес и менеджмент" МГТУ им. Н.Э.Баумана.
Проверка однородности двух независимых выборок
1. В первой случайной репрезентативной выборке объема  положительный ответ дали
положительный ответ дали  опрошенных (респондентов), а во второй случайной репрезентативной выборке объема
опрошенных (респондентов), а во второй случайной репрезентативной выборке объема 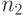 положительный ответ дали
положительный ответ дали 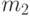 опрошенных. Указать доверительные границы для долей (вероятностей положительного ответа в соответствующих генеральных совокупностях) с доверительной вероятностью 0.95 и проверить гипотезу о равенстве долей (уровень значимости
опрошенных. Указать доверительные границы для долей (вероятностей положительного ответа в соответствующих генеральных совокупностях) с доверительной вероятностью 0.95 и проверить гипотезу о равенстве долей (уровень значимости 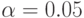 ):
):
2. Для двух независимых выборок объемов  и
и 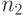 даны выборочные средние арифметические
даны выборочные средние арифметические 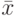 и
и 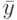 выборочные средние квадратические отклонения
выборочные средние квадратические отклонения  соответственно. Указать доверительные границы для математических ожиданий (с доверительной вероятностью 0.95) и проверить гипотезу о равенстве математических ожиданий с помощью критерия Крамера-Уэлча (уровень значимости
соответственно. Указать доверительные границы для математических ожиданий (с доверительной вероятностью 0.95) и проверить гипотезу о равенстве математических ожиданий с помощью критерия Крамера-Уэлча (уровень значимости 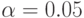 ):
):
 |
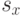 |
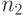 |
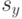 |
|||
|---|---|---|---|---|---|---|
| Вариант 1 | 100 | 13,7 | 7,3 | 200 | 12,1 | 2,5 |
| Вариант 2 | 213 | 10,3 | 5,3 | 308 | 12,2 | 1,7 |
3. Проверить гипотезу об однородности функций распределения с помощью критерия Вилкоксона (на уровне значимости 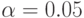 ):
):
| 1 выборка | 33 | 27 | 12 | 27 | 39 | 42 | 47 | 48 | 50 | 32 |
| 2 выборка | 11 | 20 | 30 | 31 | 22 | 18 | 17 | 25 | 28 | 29 |
Проверка однородности связанных выборках
4. Для каждого из  объектов даны значения
объектов даны значения  и
и 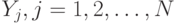 , результатов измерений (наблюдений, испытаний, анализов, опытов) двух признаков. Необходимо проверить, есть ли значимое различие между значениями двух признаков или же это различие может быть объяснено случайными отклонениям значений признаков. Другими словами, требуется проверить однородность (т.е. отсутствие различия) связанных выборок.
, результатов измерений (наблюдений, испытаний, анализов, опытов) двух признаков. Необходимо проверить, есть ли значимое различие между значениями двух признаков или же это различие может быть объяснено случайными отклонениям значений признаков. Другими словами, требуется проверить однородность (т.е. отсутствие различия) связанных выборок.
 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
 |
74 | 79 | 65 | 69 | 71 | 66 | 71 | 73 | 72 | 68 |
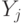 |
73 | 65 | 71 | 69 | 70 | 69 | 78 | 70 | 60 | 62 |
 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
 |
70 | 69 | 76 | 74 | 72 | 69 | 74 | 72 | 77 | 75 |
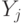 |
61 | 67 | 73 | 67 | 73 | 64 | 67 | 65 | 63 | 70 |
Проверку однородности на уровне значимости 0,05 проведите с помощью трех критериев:
- критерия знаков (основанного на проверке гипотезы
 для биномиального распределения с использованием теоремы Муавра-Лапласа);
для биномиального распределения с использованием теоремы Муавра-Лапласа); - критерия для проверки равенства 0 математического ожидания (критерий основан на асимптотической нормальности выборочного среднего арифметического, деленного на выборочное среднее квадратическое отклонение);
- критерия Орлова (типа омега-квадрат) для проверки гипотезы симметрии функции распределения (разности результатов измерений, наблюдений, испытаний, анализов, опытов для двух признаков) относительно 0.
Метод наименьших квадратов
5. Исходные данные - набор  пар чисел (
пар чисел ( 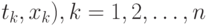 , где
, где  - независимая переменная (например, время), а
- независимая переменная (например, время), а  - зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостью
- зависимая (например, индекс инфляции). Предполагается, что переменные связаны зависимостью
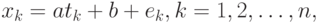
где  и
и  - параметры, неизвестные статистику и подлежащие оцениванию, а
- параметры, неизвестные статистику и подлежащие оцениванию, а  - погрешности, искажающие зависимость.
- погрешности, искажающие зависимость.
-
Методом наименьших квадратов оцените параметры
 и
и  линейной зависимости. Выпишите восстановленную зависимость.
линейной зависимости. Выпишите восстановленную зависимость. - Вычислите восстановленные значения зависимой переменной, сравните их с исходными значениями (найдите разности) и проверьте условие точности вычислений (при отсутствии ошибок в вычислениях сумма исходных значений должна равняться сумме восстановленных).
- Найдите остаточную сумму квадратов и оцените дисперсию погрешностей.
- Выпишите точечный прогноз, а также верхнюю и нижнюю доверительные границы для него (для доверительной вероятности 0,95).
- Рассчитайте прогнозное значение и доверительные границы для него для момента
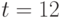 .
. - Как изменятся результаты, если доверительная вероятность будет увеличена? А если она будет уменьшена?
Индекс инфляции
6. На основе данных табл.6 рассчитайте индекс инфляции с 14.03.1991 по 14.03.2001 на основе потребительской корзины из продуктов №№ 3, 5, 8, 13, 21, 25.
| № п/п | Наименование продукта питания | Годовая норма, кг | Цена на 14.03.1991 | Цена на 14.03.2001 |
|---|---|---|---|---|
| 1 | Хлеб пшеничный | 59,8 | 0-50 | 12 |
| 2 | Хлеб ржаной | 65,3 | 0-20 | 10 |
| 3 | Мука пшеничная | 18,5 | 0-46 | 10 |
| 4 | Картофель | 124,22 | 0-10 | 9 |
| 5 | Капуста | 30,4 | 0-20 | 8 |
| 6 | Помидоры | 2,8 | 0-85 | 80 |
| 7 | Столовые корнеплоды | 40,6 | 0-20 | 9 |
| 8 | Прочие (лук) | 27,9 | 0-50 | 8 |
| 9 | Яблоки свежие | 15,1 | 1-50 | 20 |
| 10 | Сахар | 19,0 | 0-90 | 21 |
| 11 | Говядина | 4,4 | 2-00 | 85 |
| 12 | Субпродукты (печень) | 0,5 | 1-40 | 45 |
| 13 | Птица | 16,1 | 2-40 | 52 |
| 14 | Колбаса докторская | 0,4 | 2-30 | 95 |
| 15 | Копчености | 0,3 | 3-70 | 200 |
| 16 | Рыба свежая (минтай) | 10,9 | 0-37 | 80 |
| 17 | Сельди | 0,8 | 1-40 | 40 |
| 18 | Молоко, кефир | 110,0 | 0-32 | 17 |
| 19 | Сметана, сливки | 1,6 | 1-70 | 50 |
| 20 | Масло животное | 2,5 | 3-60 | 70 |
| 21 | Творог | 9,8 | 1-00 | 45 |
| 22 | Сыр и брынза | 2,3 | 3-60 | 70 |
| 23 | Яйца, десяток | 15,2 | 0-90 | 20 |
| 24 | Масло растительное | 3,8 | 1-80 | 26 |
| 25 | Маргарин | 6,3 | 1-20 | 35 |


