| ВКР |
Преподаватель
Вы можете этот курс.
Опубликован: 17.07.2009 | Уровень: специалист | Доступ: платный
Лекция 4:
Методы принятия решений
Теория графов и оптимизация
Один из разделов дискретной математики, часто используемый при принятии решений - теория графов. Граф - это совокупность точек, называемых вершинами графа, некоторые из которых соединены дугами. Примеры графов приведены на рис.4.5.
На только что введенное понятие графа "навешиваются" новые свойства. Исходному объекту приписывают новые качества. Например, вводится и используется понятие ориентированного графа. В таком графе дуги имеют стрелки, направленные от одной вершины к другой. Примеры ориентированных графов даны на рис.4.6.
Ориентированный граф был бы полезен, например, для иллюстрации организации перевозок в транспортной задаче. В экономике дугам ориентированного или обычного графа часто приписывают числа, например, стоимость проезда или перевозки груза из пункта А (начальная вершина дуги) в пункт Б (конечная вершина дуги).
Рассмотрим несколько типичных задач принятия решений, связанных с оптимизацией на графах.
Задача коммивояжера.Требуется посетить все вершины графа и вернуться в исходную вершину, минимизировав затраты на проезд (или минимизировав время).
Исходные данные здесь - это граф, дугам которого приписаны положительные числа - затраты на проезд или время, необходимое для продвижения из одной вершины в другую. В общем случае граф является ориентированным, и каждые две вершины соединяют две дуги - туда и обратно. Действительно, если пункт А расположен на горе, а пункт Б - в низине, то время на проезд из А в Б, очевидно, меньше времени на обратный проезд из Б в А.
Многие постановки экономического содержания сводятся к задаче коммивояжера. Например:
- составить наиболее выгодный маршрут обхода наладчика в цехе (контролера, охранника, милиционера), отвечающего за должное функционирование заданного множества объектов (каждый из этих объектов моделируется вершиной графа);
- составить наиболее выгодный маршрут доставки деталей рабочим или хлеба с хлебозавода по заданному числу булочных и других торговых точек (парковка у хлебозавода).
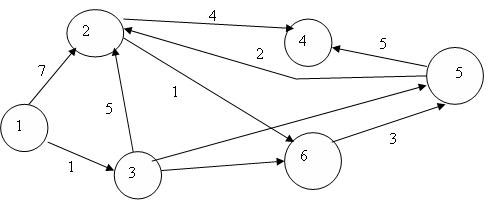
Задача о кратчайшем пути. Как кратчайшим путем попасть из одной вершины графа в другую? В терминах производственного менеджмента: как кратчайшим путем (и, следовательно, с наименьшим расходом топлива и времени, наиболее дешево) попасть из пункта А в пункт Б? Для решения этой задачи каждой дуге ориентированного графа должно быть сопоставлено число - время движения по этой дуге от начальной вершины до конечной. Рассмотрим пример (рис.4.7).
Ситуацию можно описать не только ориентированным графом с весами, приписанными дугам, но и таблицей (табл.4.7).
| Начало дуги | Конец дуги | Время в пути |
|---|---|---|
| 1 | 2 | 7 |
| 1 | 3 | 1 |
| 2 | 3 | 4 |
| 2 | 6 | 1 |
| 3 | 2 | 5 |
| 3 | 5 | 2 |
| 3 | 6 | 3 |
| 5 | 2 | 2 |
| 5 | 4 | 5 |
| 6 | 5 | 3 |
Спрашивается в задаче: как кратчайшим путем попасть из вершины 1 в вершину 4?
Решение. Введем обозначение: С(Т) - длина кратчайшего пути из вершины 1 в вершину Т. (Поскольку любой путь, который надо рассмотреть, состоит из дуг, а дуг конечное число, и каждая входит не более одного раза, то претендентов на кратчайший путь конечное число, и минимум из конечного числа элементов всегда достигается.) Рассматриваемая задача состоит в вычислении С(4) и указании пути, на котором этот минимум достигается.
Для исходных данных, представленных на рис.4.7 и в табл.4.6, в вершину 3 входит только одна стрелка, как раз из вершины 1, и около этой стрелки стоит ее длина, равная 1, поэтому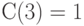 
. Кроме того, очевидно, что 
.
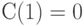В вершину 4 можно попасть либо из вершины 2, пройдя путь, равный 4, либо из вершины 5, пройдя путь, равный 5. Поэтому справедливо соотношение
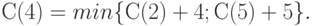
Таким образом, проведена реструктуризация задачи - нахождение С(4) сведено к нахождению С(2) и С(5).
В вершину 5 можно попасть либо из вершины 3, пройдя путь, равный 2, либо из вершины 6, пройдя путь, равный 3. Поэтому справедливо соотношение
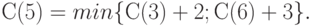
Мы знаем, что 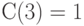. Поэтому
Поскольку очевидно, что С(6) - положительное число, то из последнего соотношения вытекает, что С(5) = 3.
В вершину 2 можно попасть либо из вершины 1, пройдя путь, равный 7, либо из вершины 3, пройдя путь, равный 5, либо из вершины 5, пройдя путь, равный 2. Поэтому справедливо соотношение
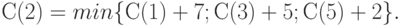
Нам известно, что 
. Поэтому
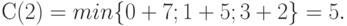
Теперь мы можем найти С(4):
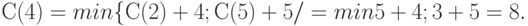
Таким образом, длина кратчайшего пути равна 8. Из последнего соотношения ясно, что в вершину 4 надо идти через вершину 5. Возвращаясь к вычислению С(5), видим, что в вершину 5 надо идти через вершину 3. А в вершину 3 можно попасть только из вершины 1. Итак, кратчайший путь таков:
Задача о кратчайшем пути для конкретных исходных данных (рис.4.77 и табл.4.7) полностью решена.
Оптимизационные задачи на графах, возникающие при подготовке управленческих решений в производственном менеджменте, весьма многообразны. Рассмотрим в качестве примера еще одну задачу, связанную с перевозками.
Задача о максимальном потоке. Как (т.е. по каким маршрутам) послать максимально возможное количество грузов из начального пункта в конечный пункт, если пропускная способность путей между пунктами ограничена?
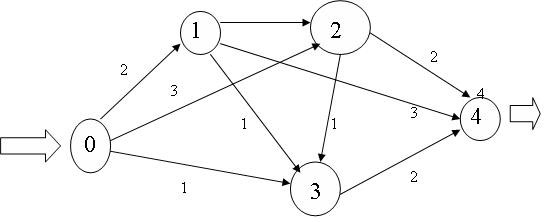
Для решения этой задачи каждой дуге ориентированного графа, соответствующего транспортной системе, должно быть сопоставлено число - пропускная способность этой дуги. Рассмотрим пример (рис.4.8).
Исходные данные о транспортной системе, например, внутризаводской, приведенные на рис.4.8, можно также задать таблицей (табл.4.8).
| Пункт отправления | Пункт назначения | Пропускная способность |
|---|---|---|
| 0 | 1 | 2 |
| 0 | 2 | 3 |
| 0 | 3 | 1 |
| 1 | 2 | 4 |
| 1 | 3 | 1 |
| 1 | 4 | 3 |
| 2 | 3 | 1 |
| 2 | 4 | 2 |
| 3 | 4 | 2 |
Решение задачи о максимальном потоке может быть получено из следующих соображений.
Очевидно, максимальная пропускная способность транспортной системы не превышает 6, поскольку не более 6 единиц грузов можно направить из начального пункта 0, а именно, 2 единицы в пункт 1, 3 единицы в пункт 2 и 1 единицу в пункт 3.
Далее надо добиться, чтобы все 6 вышедших из пункта 0 единиц груза достигли конечного пункта 4. Очевидно, 2 единицы груза, пришедшие в пункт 1, можно непосредственно направить в пункт 4. Пришедшие в пункт 2 грузы придется разделить: 2 единицы сразу направить в пункт 4, а 1 единицу - в промежуточный пункт 3 (из-за ограниченной пропускной способности участка между пунктами 2 и 4). В пункт 3 доставлены такие грузы: 1 единица из пункта 0 и 1 единица из пункта 3. Их направляем в пункт 4.
Итак, максимальная пропускная способность рассматриваемой транспортной системы - 6 единиц груза. При этом не используются внутренние участки (ветки) между пунктами 1 и 2, а также между пунктами 1 и 3. Не догружена ветка между пунктами 1 и 4 - по ней направлены 2 единицы груза при пропускной способности в 3 единицы.
Решение можно представить в виде таблицы (табл.4.9).
| Пункт отправления | Пункт назначения | План перевозок | Пропускная способность |
|---|---|---|---|
| 0 | 1 | 2 | 2 |
| 0 | 2 | 3 | 3 |
| 0 | 3 | 1 | 1 |
| 1 | 2 | 0 | 4 |
| 1 | 3 | 0 | 1 |
| 1 | 4 | 2 | 3 |
| 2 | 3 | 1 | 1 |
| 2 | 4 | 2 | 2 |
| 3 | 4 | 2 | 2 |
Задача линейного программирования при максимизации потока. Дадим формулировку задачи о максимальном потоке в терминах линейного программирования. Пусть ХKM - объем перевозок из пункта К в пункт М. Согласно рис.4.8 К = 0,1,2,3, М = 1,2,3,4, причем перевозки возможны лишь в пункт с большим номером. Значит, всего имеется 9 переменных 
а именно, 
Задача линейного программирования, нацеленная на максимизацию потока, имеет вид:
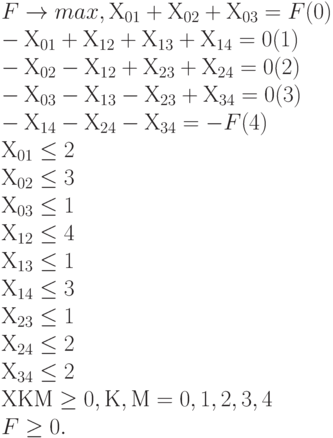
Здесь F - целевая функция, условие (0) описывает вхождение грузов в транспортную систему. Условия (1) - (3) задают балансовые соотношения для узлов 1- 3 системы. Другими словами, для каждого из внутренних узлов входящий поток грузов равен выходящему потоку, грузы не скапливаются внутри и системы и не "рождаются" в ней. Условие (4) - это условие "выхода" грузов из системы. Вместе с условием (0) оно составляет балансовое соотношение для системы в целом ("вход" равен "выходу"). Следующие девять неравенств задают ограничения на пропускную способность отдельных "веток" транспортной системы. Затем указана неотрицательность объемов перевозок и целевой функции. Ясно, что последнее неравенство вытекает из вида целевой функции (соотношения (0) или (4)) и неотрицательности объемов перевозок. Однако последнее неравенство несет некоторую общую информацию - через систему может быть пропущен либо положительный объем грузов, либо нулевой (например, если внутри системы происходит движение по кругу), но не отрицательный (он не имеет экономического смысла, но формальная математическая модель об этом "не знает").
О многообразии оптимизационных задач. В различных проблемах принятия решений возникают самые разнообразные задачи оптимизации. Для их решения применяются те или иные методы, точные или приближенные. Задачи оптимизации часто используются в теоретико-экономических исследованиях. Достаточно вспомнить оптимизацию экономического роста страны с помощью матрицы межотраслевого баланса Василия Леонтьева или микроэкономические задачи определения оптимального объема выпуска по функции издержек при фиксированной цене (или в условиях монополии) или минимизации издержек при заданном объеме выпуска путем выбора оптимального соотношения факторов производства (с учетом платы за них).
Кроме затронутых выше методов решения задач оптимизации, напомним о том, что гладкие функции оптимизируют, приравнивая 0 производную (для функций нескольких переменных - частные производные). При наличии ограничений используют множители Лагранжа. Эти методы обычно излагаются в курсах высшей математики и потому опущены здесь.
