| ВКР |
Экспертные методы
Законы больших чисел показывают, во-первых, что медиана Кемени обладает устойчивостью по отношению к незначительному изменению состава экспертной комиссии; во-вторых, при увеличении числа экспертов она приближается к некоторому пределу. Его естественно рассматривать как истинное мнение экспертов, от которого каждый из них несколько отклонялся по случайным причинам. Рассматриваемый здесь закон больших чисел является обобщением известного в статистике "классического" закона больших чисел. Он основан на иной математической базе - теории оптимизации, в то время как "классический" закон больших чисел использует суммирование. Упорядочения и другие бинарные отношения нельзя складывать, поэтому приходится применять иную математику.
Вычисление медианы Кемени - задача целочисленного программирования. В частности, для ее нахождения используется различные алгоритмы дискретной математики, в частности, основанные на методе ветвей и границ. Применяют также алгоритмы, основанные на идее случайного поиска, поскольку для каждого бинарного отношения нетрудно найти множество его соседей.
Рассмотрим упрощенный пример вычисления медианы Кемени. Пусть дана квадратная матрица (порядка 9) попарных расстояний для множества бинарных отношений из 9 элементов  (см. табл.14.3). Пусть требуется найти в этом множестве медиану для множества из 5 элементов
(см. табл.14.3). Пусть требуется найти в этом множестве медиану для множества из 5 элементов 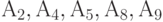 .
.
| 0 | 2 | 13 | 1 | 7 | 4 | 10 | 3 | 11 |
| 2 | 0 | 5 | 6 | 1 | 3 | 2 | 5 | 1 |
| 13 | 5 | 0 | 2 | 2 | 7 | 6 | 5 | 7 |
| 1 | 6 | 2 | 0 | 5 | 4 | 3 | 8 | 8 |
| 7 | 1 | 2 | 5 | 0 | 10 | 1 | 3 | 7 |
| 4 | 3 | 2 | 5 | 0 | 10 | 1 | 3 | 7 |
| 4 | 3 | 7 | 4 | 10 | 0 | 2 | 1 | 5 |
| 10 | 2 | 6 | 3 | 1 | 2 | 0 | 6 | 3 |
| 3 | 5 | 5 | 8 | 3 | 1 | 6 | 0 | 9 |
| 11 | 1 | 7 | 8 | 7 | 5 | 3 | 9 | 0 |
В соответствии с определением медианы Кемени следует ввести в рассмотрение функцию

рассчитать ее значения для всех 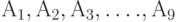 и выбрать наименьшее. Проведем расчеты:
и выбрать наименьшее. Проведем расчеты:

Из всех вычисленных сумм наименьшая равна 13, и достигается она при  , следовательно, медиана Кемени - это множество
, следовательно, медиана Кемени - это множество  , состоящее из одного элемента
, состоящее из одного элемента  .
.
Контрольные вопросы и задачи
- Почему необходимо применение экспертных оценок при решении технических, организационных, экономических, экологических и иных проблем?
- Какие стадии экспертного исследования выделяет менеджер - организатор такого исследования?
- По каким основаниям классифицируют различные варианты организации экспертных исследований?
- Какова роль диссидентов в различных видах экспертиз?
- Какой вид могут иметь ответы экспертов?
- Чем метод средних арифметических рангов отличает от метода медиан рангов?
- Почему необходимо согласование кластеризованных ранжировок и как оно проводится?
- В чем состоит проблема согласованности ответов экспертов?
- Как бинарные отношения используются в экспертизах?
- Как бинарные отношения описываются матрицами из 0 и 1?
- Что такое расстояние Кемени и медиана Кемени?
- Чем закон больших чисел для медианы Кемени отличается от "классического" закона больших чисел, известного в статистике?
-
В табл. 14.4 приведены упорядочения 7 инвестиционных проектов, представленные 7 экспертами.
Таблица 14.4. Упорядочения проектов экспертами Эксперты Упорядочения 1 1 < {2,3} < 4 < 5 < {6,7} 2 {1,3} < 4 < 2< 5< 7 < 6 3 1 < 4 < 2 < 3 < 6 < 5 < 7 4 1 < {2, 4} < 3 < 5 < 7 <6 5 2 < 3 < 4 < 5 <1 <6 <7 6 1 < 3 < 2 < 5 < 6 < 7 < 4 7 1 < 5 < 3 < 4 < 2 < 6 < 7 Найдите:
а) итоговое упорядочение по средним арифметическим рангам;
б) итоговое упорядочение по медианам рангов;
в) кластеризованную ранжировку, согласующую эти два упорядочения.
- Выпишите матрицу из 0 и 1, соответствующую бинарному отношению (кластеризованной ранжировке)
 .
. - Найдите расстояние Кемени между бинарными отношениями - упорядочениями
![А = [3< 2 <1< {4,5}]](/sites/default/files/tex_cache/ed401eebd7560b8beb892784d0f6d93b.png) и
и ![B = [1 < {2 ,3} < 4 < 5 ]](/sites/default/files/tex_cache/a60ac96a1fb4e798eadbfc10b78e466f.png) .
. -
Дана квадратная матрица (порядка 9) попарных расстояний (мер различия) для множества бинарных отношений из 9 элементов
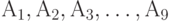 (табл.14.5). Найдите в этом множестве медиану для множества из 5 элементов
(табл.14.5). Найдите в этом множестве медиану для множества из 5 элементов 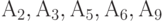 .
.
Темы докладов и рефератов
- Роль экспертных методов в менеджменте.
- Организация различных видов экспертных исследований.
- Сравнение очных и заочных вариантов работы экспертов.
- Методы средних баллов.
- Согласование кластеризованных ранжировок.
- Методы теории люсианов в экспертных оценках.
- Классификация мнений экспертов и проверка согласованности.
- Использование люсианов в теории и практике экспертных оценок.
- Формирование итогового мнения комиссии экспертов.
- Расстояние по Кемени и медиана Кемени в экспертных оценках.
- Законы больших чисел в пространствах нечисловой природы.

