| ВКР |
Методы оптимизации
В настоящее время менеджер может использовать при принятии решения различные компьютерные и математические средства. В памяти компьютеров держат массу информации, организованную с помощью баз данных и других программных продуктов, позволяющих оперативно ею пользоваться. Экономико-математические и эконометрические модели позволяют просчитывать последствия тех или иных решений, прогнозировать развитие событий. Методы экспертных оценок, о которых пойдет речь ниже, также весьма математизированы и используют компьютеры.
Наиболее часто используются оптимизационные модели принятия решений. Их общий вид таков:
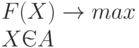
Здесь  - параметр, который менеджер может выбирать (управляющий параметр). Он может иметь различную природу - число, вектор, множество и т.п. Цель менеджера - максимизировать целевую функцию
- параметр, который менеджер может выбирать (управляющий параметр). Он может иметь различную природу - число, вектор, множество и т.п. Цель менеджера - максимизировать целевую функцию 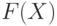 , выбрав соответствующий
, выбрав соответствующий  .. При этом он должен учитывать ограничения
.. При этом он должен учитывать ограничения  на возможные значения управляющего параметра
на возможные значения управляющего параметра  - он должен лежать в множестве
- он должен лежать в множестве  . Ряд примеров оптимизационных задач менеджмента приведен ниже.
. Ряд примеров оптимизационных задач менеджмента приведен ниже.
Линейное программирование
Среди оптимизационных задач менеджмента наиболее известны задачи линейного программирования, в которых максимизируемая функция 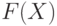 является линейной, а ограничения
является линейной, а ограничения  задаются линейными неравенствами. Начнем с примера.
задаются линейными неравенствами. Начнем с примера.
Производственная задача. Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола - 20 единиц (футов красного дерева). Стул требует 10 человеко-часов, стол - 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула - 45 долларов США, при производстве стола - 80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?
Обозначим:  - число изготовленных стульев,
- число изготовленных стульев, 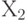 - число сделанных столов. Задача оптимизации имеет вид:
- число сделанных столов. Задача оптимизации имеет вид:

В первой строке выписана целевая функция - прибыль при выпуске  стульев и
стульев и 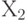 столов. Ее требуется максимизировать, выбирая оптимальные значения переменных
столов. Ее требуется максимизировать, выбирая оптимальные значения переменных  и
и 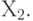 При этом должны быть выполнены ограничения по материалу (вторая строчка) - истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) - затрачено не более 450 часов. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если
При этом должны быть выполнены ограничения по материалу (вторая строчка) - истрачено не более 400 футов красного дерева. А также и ограничения по труду (третья строчка) - затрачено не более 450 часов. Кроме того, нельзя забывать, что число столов и число стульев неотрицательны. Если  , то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то
, то это значит, что стулья не выпускаются. Если же хоть один стул сделан, то  положительно. Но невозможно представить себе отрицательный выпуск -
положительно. Но невозможно представить себе отрицательный выпуск -  не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
не может быть отрицательным с экономической точки зрения, хотя с математической точки зрения такого ограничения усмотреть нельзя. В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.
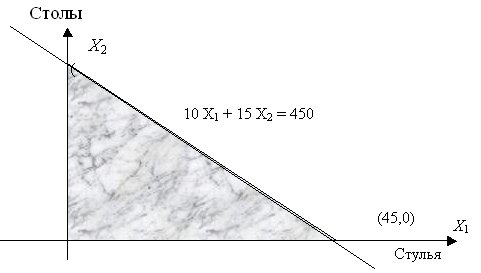
Условия производственной задачи можно изобразить на координатной плоскости. Будем по горизонтальной оси абсцисс откладывать значения 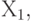 а по вертикальной оси ординат - значения
а по вертикальной оси ординат - значения 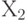 . Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения
. Тогда ограничения по материалу и последние две строчки оптимизационной задачи выделяют возможные значения 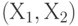 объемов выпуска в виде треугольника (рис.12.1).
объемов выпуска в виде треугольника (рис.12.1).
Таким образом, ограничения по материалу изображаются в виде выпуклого многоугольника, конкретно, треугольника. Этот треугольник получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей второй строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось  , соответствующую стульям, в точке (80,0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось
, соответствующую стульям, в точке (80,0). Это означает, что если весь материал пустить на изготовление стульев, то будет изготовлено 80 стульев. Та же прямая пересекает ось 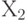 , соответствующую столам, в точке (0,20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - материал останется.
, соответствующую столам, в точке (0,20). Это означает, что если весь материал пустить на изготовление столов, то будет изготовлено 20 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - материал останется.
Аналогичным образом можно изобразить и ограничения по труду (рис.12.1).
Таким образом, ограничения по труду, как и ограничения по материалу, изображаются в виде треугольника. Этот треугольник также получается путем отсечения от первого квадранта примыкающей к началу координат зоны. Отсечение проводится прямой, соответствующей третьей строке исходной задачи, с заменой неравенства на равенство. Прямая пересекает ось  , соответствующую стульям, в точке (45,0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось
, соответствующую стульям, в точке (45,0). Это означает, что если все трудовые ресурсы пустить на изготовление стульев, то будет сделано 45 стульев. Та же прямая пересекает ось 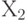 , соответствующую столам, в точке (0,30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - часть рабочих будет простаивать.
, соответствующую столам, в точке (0,30). Это означает, что если всех рабочих поставить на изготовление столов, то будет сделано 30 столов. Для всех точек внутри треугольника выполнено неравенство, а не равенство - часть рабочих будет простаивать.
Мы видим, что очевидного решения нет - для изготовления 80 стульев есть материал, но не хватает рабочих рук, а для производства 30 столов есть рабочая сила, но нет материала, Значит, надо изготавливать и то, и другое. Но в каком соотношении?
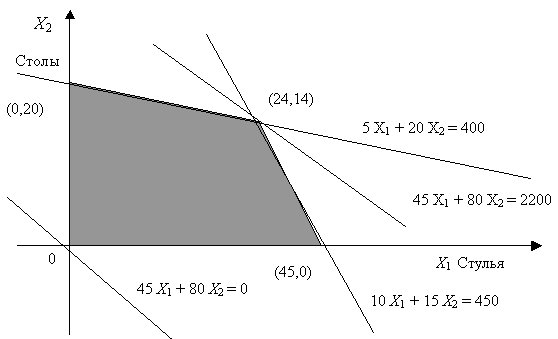
Чтобы ответить на этот вопрос, надо "совместить" рис.12.1 и рис.12.2, получив область возможных решений, а затем проследить, какие значения принимает целевая функция на этом множестве (рис.12.3).
Таким образом, множество возможных значений объемов выпуска стульев и столов 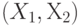 , или, в других терминах, множество
, или, в других терминах, множество  , задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис.12.1. Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис.12.1 и рис.12.2, т.е. решение системы уравнений
, задающее ограничения на параметр управления в общей оптимизационной задаче, представляет собой пересечение двух треугольников, т.е. выпуклый четырехугольник, показанный на рис.12.1. Три его вершины очевидны - это (0,0), (45,0) и (0,20). Четвертая - это пересечение двух прямых - границ треугольников на рис.12.1 и рис.12.2, т.е. решение системы уравнений
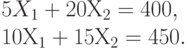
Из первого уравнения:  . Подставляем во второе уравнение:
. Подставляем во второе уравнение:
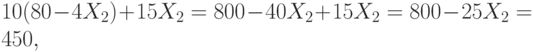
следовательно,  , откуда
, откуда 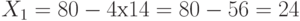 . Итак, четвертая вершина четырехугольника - это (24, 14).
. Итак, четвертая вершина четырехугольника - это (24, 14).
Надо найти максимум линейной функции на выпуклом многоугольнике. (В общем случае линейного программирования - максимум линейной функции на выпуклом многограннике, лежащем в конечномерном линейном пространстве.) Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. В общем случае - в одной вершине, и это - единственная точка максимума. В частном - в двух, и тогда отрезок, их соединяющий, тоже состоит из точек максимума.
Целевая функция  принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24,14) она принимает значение 2200. При этом прямая
принимает минимальное значение, равное 0, в вершине (0,0). При увеличении аргументов эта функция увеличивается. В вершине (24,14) она принимает значение 2200. При этом прямая 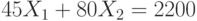 проходит между прямыми ограничений
проходит между прямыми ограничений 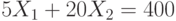 и
и  , пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24,14).
, пересекающимися в той же точке. Отсюда, как и из непосредственной проверки двух оставшихся вершин, вытекает, что максимум целевой функции, равный 2200, достигается в вершине (24,14).
Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.
Двойственная задача. Каждой задаче линейного программирования соответствует так называемая двойственная задача. В ней по сравнению с исходной задачей строки переходят в столбцы, неравенства меняют знак, вместо максимума ищется минимум (или, наоборот, вместо минимума - максимум). Задача, двойственная к двойственной - эта сама исходная задача. Сравним исходную задачу (слева) и двойственную к ней (справа):
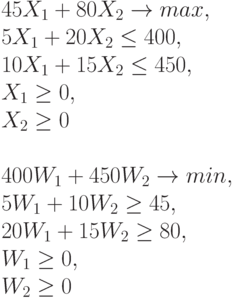
Почему двойственная задача столь важна? Можно доказать, что оптимальные значения целевых функций в исходной и двойственной задачах совпадают (т.е. максимум в исходной задаче совпадает с минимумом в двойственной). При этом оптимальные значения 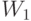 и
и 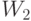 показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства,
показывают стоимость материала и труда соответственно, если их оценивать по вкладу в целевую функцию. Чтобы не путать с рыночными ценами этих факторов производства, 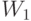 и
и 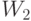 называют "объективно обусловленными оценками" сырья и рабочей силы.
называют "объективно обусловленными оценками" сырья и рабочей силы.
Линейное программирование как научно-практическая дисциплина. Из всех задач оптимизации задачи линейного программирования выделяются тем, что в них ограничения - системы линейных неравенств или равенств. Ограничения задают выпуклые линейные многогранники в конечном линейном пространстве. Целевые функции также линейны.
Впервые такие задачи решались советским математиком Л.В. Канторовичем (1912-1986) в 1930-х годах как задачи производственного менеджмента с целью оптимизации организации производства и производственных процессов, например, процессов загрузки станков и раскройки листов материалов. После второй мировой войны аналогичными задачами занялись в США. В 1975 г. Т. Купманс (1910-1985, родился в Нидерландах, работал в основном в США) и академик АН СССР Л.В. Канторович были награждены Нобелевскими премиями по экономике.
Рассмотрим несколько типовых задач линейного программирования .
Задача о диете (упрощенный вариант). Предположим для определенности, что необходимо составить самый дешевый рацион питания цыплят, содержащий необходимое количество определенных питательных веществ (для простоты, тиамина Т и ниацина Н).
Пищевая ценность рациона (в калориях) должна быть не менее заданной. Пусть для простоты смесь для цыплят изготавливается из двух продуктов - К и С. Известно содержание тиамина и ниацина в этих продуктах, а. также питательная ценность К и С (в калориях). Сколько К и С надо взять для одной порции куриного корма, чтобы цыплята получили необходимую им дозу веществ Н и Т и калорий (или больше), а стоимость порции была минимальна? Исходные данные для расчетов приведены в табл.12.1.
Задача линейного программирования имеет вид:
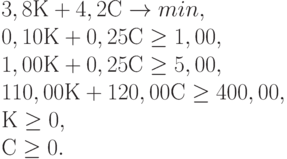
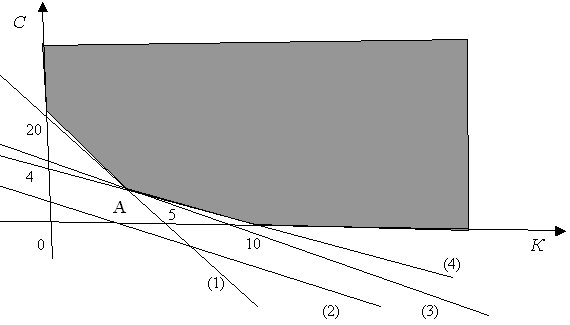
Ее графическое решение представлено на рис.4. Ради облегчения восприятия четыре прямые обозначены номерами (1) - (4). Прямая (1) - это прямая 1,00 К + 0,25 С = 5,00 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5,0) на оси абсцисс и (0,20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования.
Прямая (2) - это прямая 110,00 К + 120,00 С = 400,00 (ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при К = 0, прямая (1) проходит через точку (0,20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений
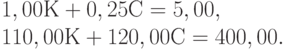
Из первого уравнения  . Подставим во второе:
. Подставим во второе: 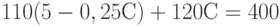 , откуда
, откуда  . Следовательно,
. Следовательно,  , т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничения по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С точки зрения менеджера они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.
, т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничения по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С точки зрения менеджера они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.
Прямая (4) - это прямая 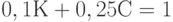 (ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10,0) на оси абсцисс и (0,4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).
(ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10,0) на оси абсцисс и (0,4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).
Следовательно, область допустимых значений параметров (К, С) является неограниченной сверху. Из всей плоскости она выделяется осями координат (лежит в первом квадранте) и прямыми (1) и (4) (лежит выше этих прямых, а также включает граничные отрезки). Область допустимых значений параметров, т.е. точек (К, С), можно назвать "неограниченным многоугольником". Минимум целевой функции  может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10,0) и ординат (0,20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений
может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10,0) и ординат (0,20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений
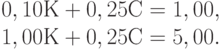
Из второго уравнения  , из первого
, из первого 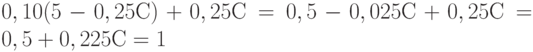 , откуда
, откуда 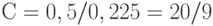 и
и 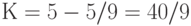 . Итак,
. Итак, 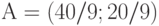 .
.
Прямая (3) на рис.4 - это прямая, соответствующая целевой функции  Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен
Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен  . Задача об оптимизации смеси полностью решена.
. Задача об оптимизации смеси полностью решена.
Двойственная задача, построенная по описанным выше правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи):
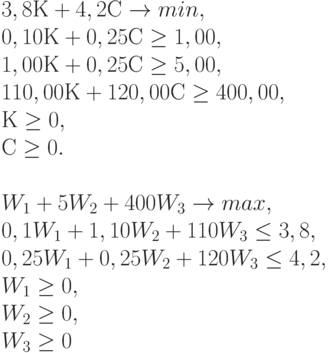
Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т.е. оба числа равны  . Интерпретация двойственных переменных:
. Интерпретация двойственных переменных: 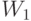 - "стоимость" единицы вещества
- "стоимость" единицы вещества  , а
, а 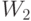 - "стоимость" единицы вещества
- "стоимость" единицы вещества  , измеренные "по их вкладу" в целевую функцию. При этом
, измеренные "по их вкладу" в целевую функцию. При этом 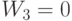 , поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак,
, поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, 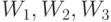 - это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
- это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары. В табл.12.2 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий).
| Кухни | Кофеварки | Самовары | |
|---|---|---|---|
| Штамповка | 20000 | 30000 | 12000 |
| Отделка | 30000 | 10000 | 10000 |
| Сборка | 20000 | 12000 | 8000 |
| Объем выпуска |  |
 |
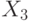 |
| Удельная прибыль (на одно изделие) | 15 | 12 | 14 |
При этом штамповка и отделка проводятся на одном и том же оборудовании. Оно позволяет штамповать за заданное время или 20000 кухонь, либо 30000 кофеварок, либо и то, и другое, не в меньшем количестве. А вот сборка проводится на отдельных участках.
Задача линейного программирования имеет вид:
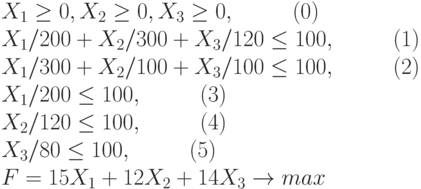
Здесь:
(0) - обычное в экономике условие неотрицательности переменных,
(1) - ограничение по возможностям штамповки (выраженное для облегчения восприятия в процентах),
(2) - ограничение по возможностям отделки,
(3) - ограничение по сборке для кухонь,
(4) - то же для кофемолок,
(5) - то же для самоваров (как уже говорилось, все три вида изделий собираются на отдельных линиях).
Наконец, целевая функция F - общая прибыль предприятия.
Заметим, что неравенство (3) вытекает из неравенства (1), а неравенство (4) - из (2). Поэтому неравенства (3) и (4) можно из формулировки задачи линейного программирования исключить.
Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане 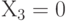 , т.е. самовары выпускать невыгодно.
, т.е. самовары выпускать невыгодно.