| ВКР |
Инструменты менеджмента
Декомпозиция задач принятия решений "от ветвей к корню". До сих пор мы разбирали ситуации, когда задача принятия решения разбивалась на составляющие (с целью уточнения постановки и выбора одной из конкретных формулировок либо с целью разделить одну большую задачу на ряд более мелких). Рассмотрим теперь противоположный процесс, когда конкретные потребности бизнес-процессов организации порождают единый комплекс задач принятия решений.
Пример 4. Рассмотрим процесс декомпозиция задач принятия решений "от ветвей к корню" на примере формирования задач службы контроллинга организации. Для многих организаций актуальны следующие проблемы.
1) Отсутствие оперативной информации о производственных процессах требует внедрения на предприятии системы производственного учета.
2) Высокий уровень накладных расходов в общей сумме затрат заставляет заниматься выявлением мест возникновения "ненужных" затрат.
3) Излишне большая величина незавершенного производства влечет необходимость разработки системы управления заказами.
4) Отсутствует эффективный механизм контроля над деятельностью службы закупок. Имеется лишь эпизодический контроль со стороны руководства организации. Это обуславливает необходимость разработки внутри организации организационно-экономического механизма, позволяющего контролировать уровень цен на закупаемые материалы.
5) Накладные расходы планируются на предприятии по факту предыдущего периода. Это требует внедрения процесса бюджетирования.
6) Используемая система показателей недостаточна для управления предприятием. Следовательно, необходима разработка системы показателей финансово-хозяйственной, производственной и социальной деятельности предприятия.
7) У руководства предприятия отсутствует системное представление о деятельности предприятия. Для принятия обоснованных решений по управлению предприятием необходимо создание аналитической службы поддержки принятия таких решений.
Для решения семи перечисленных актуальных проблем принятия решений при управлении предприятием вытекает необходимость специальной интегрирующей службы - службы контроллинга. Вполне очевидно, что все "ветви" в рассматриваемой задаче декомпозиции направлены к одному "корню", и этот "корень" описывает задачи принятия решений, поддерживаемые службой контроллинга.
До сих пор в процессе декомпозиции все задачи одного уровня считались равнозначными, весовые коэффициенты не вводились. Однако иногда оказывается полезным различные варианты рассматривать с теми или иными коэффициентами.
Пример 5. Необходимо разработать процедуру принятия решений, связанных с оценкой эффективности разрабатываемого медицинского прибора (магнитного сепаратора). Для вычисления обобщенного показателя качества и технического уровня подобных приборов естественно провести декомпозицию на три задачи принятия решений о трем группам показателей:
- основные показатели назначения;
- экономические условия потребления;
- условия обслуживания.
Пусть X - оценка по первой группе показателей, Y - по второй, Z - по третьей. Первая оценка учитывается с весовым коэффициентом 0,6, вторая - 0,2, третья - также 0,2 (сумма трех весовых коэффициентов равна 1). Таким образом, обобщенный показатель качества и технического уровня медицинского прибора оценивается как
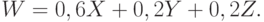
На следующем шаге декомпозиции в каждой из трех групп выделяются единичные показатели качества и технического уровня. Так, для блока "основных показателей назначения" выделяют:
1.1) степень очистки Х(1),
1.2) время очистки Х(2),
1.3) масса субстрата Х(3),
1.4) вероятность повреждения здоровых клеток Х(4).
Им также приписывают весовые коэффициенты 0,44, 0,09, 0,18, 0,29 соответственно (сумма весовых коэффициентов равна 1). Поэтому оценка по основным показателям назначения вычисляется как
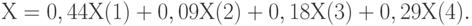
Для блока "экономические условия потребления" выделяют два единичных показателя:
2.1) методы сепарации У(1)
2.2) патентная чистота У(2).
Им также приписывают весовые коэффициенты 0,74 и 0,26 соответственно (сумма весовых коэффициентов равна 1). Поэтому оценка по экономическим условиям потребления вычисляется как
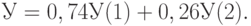
Для блока "условия обслуживания" выделяют три единичных показателя:
3.1) режим работы Z(1),
3.2.) эргономика Z(2),
3.3) надежность Z(3).
Им также приписывают весовые коэффициенты 0,55, 0,14 и 0,31 соответственно (сумма весовых коэффициентов равна 1). Поэтому оценка по блоку "условия обслуживания" вычисляется как

Таким образом, описан алгоритм декомпозиции в задаче принятия решения относительно оценки эффективности медицинского прибора. Для вычисления обобщенного показателя качества и технического уровня необходимо получить оценки девяти единичных показателей. Обычно это делают с привлечением экспертов, сопоставляющих разрабатываемый прибор с отечественными и зарубежными аналогами.
Для нахождения весовых коэффициентов обычно используют оценки экспертов. При этом для каждой группы показателей, а также при присвоении весов группам на верхнем уровне декомпозиции могут применяться свои экспертные процедуры и опрашиваться свои эксперты. Это важное преимущество рассматриваемой процедуры обеспечивается тем, что сумма весовых коэффициентов каждый раз равняется 1.
Дело в том, что из приведенных выше соотношений следует, что для вычисления обобщенного показателя качества и технического уровня можно использовать непосредственно оценки единичных показателей:
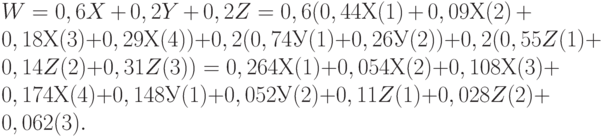
Сумма итоговых девяти весовых коэффициентов, естественно, равна 1, поскольку так построена схема декомпозиции.
С первого взгляда может показаться рациональной оценка эти девять коэффициентов непосредственно (с помощью экспертов). Из сказанного выше также ясно, что пошаговый метод декомпозиции дает возможность более точно сопоставить весовые коэффициенты (отдельно внутри групп, отдельно группы между собой), чем это можно сделать при объединении всех единичных показателей вместе.
Рассмотренные выше способы усреднения значений единичных показателей - это фактически применение средних взвешенных арифметических для значений единичных показателей. Целесообразно обратить внимание на возможность применения иных видов средних величин. А также на подходы и результаты теории измерений, позволяющие выбирать наиболее адекватные виды средних величин в соответствии с используемыми шкалами измерения.
В теории и практике принятия решений накоплено большое число различных методов подготовки и принятия решений, как относительно простых, так и основанных на изощренной математической технике. В дальнейших лекциях мы подробно рассмотрим методы принятия решений, основанных на оптимизационных, вероятностно-статистических и экспертных методах, а также познакомимся с подходами к моделированию процессов управления.
Принятие решений в условиях инфляции
Под инфляцией понимаем рост (изменение) цен. При анализе экономических процессов, протяженных во времени, необходимо переходить к сопоставимым ценам. Это невозможно сделать без расчета индекса роста цен, т.е. индекса инфляции. Проблема состоит в том, что цены на разные товары растут с различной скоростью, и необходимо эти скорости усреднять.
Рассмотрим конкретного покупателя товаров и услуг, т.е. конкретного экономического субъекта: физическое лицо, домохозяйство или фирму. Он покупает не один товар, а много. Обозначим через n количество типов товаров или услуг (далее кратко - товаров), которые он хочет и может купить. Пусть

- объемы покупок этих товаров в момент времени t по ценам:
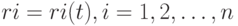
(имеется в виду цена за единицу измерения соответствующего товара, например, за штуку или килограмм...).
Подход к измерению роста цен основан на выборе и фиксации потребительской корзины 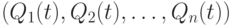 , не меняющейся со временем, т.е.
, не меняющейся со временем, т.е. 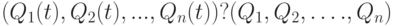 . Затем необходимо сравнить стоимости потребительской корзины
. Затем необходимо сравнить стоимости потребительской корзины 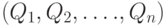 в старых
в старых 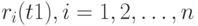 , и новых
, и новых 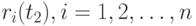 , ценах.
, ценах.
Определение. Индексом инфляции называется
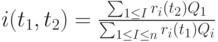
Таким образом, каждой потребительской корзине соответствует свой индекс инфляции. Однако согласно теореме сложения для индекса инфляции он является средним взвешенным арифметическим роста цен на отдельные товары. Поэтому индексы инфляции, рассчитанные по разным достаточно обширным и представительным потребительским корзинам, достаточно близки между собой.
Институт высоких статистических технологий и эконометрики (ИВСТЭ) использовал для измерения инфляции минимальную потребительскую корзину физиологически необходимых продовольственных товаров. Она была разработана на основе исходных данных Института питания Российской академии медицинских наук (РАМН). Данные о динамике индекса инфляции приведены в табл.11.7.
| № п/п | Дата снятия цен | Стоимость потребительской корзины S(t) (руб.) | Индекс инфляции I(31.3.91;t) |
|---|---|---|---|
| 1 | 31.3.91 | 26.60 | 1.00 |
| 2 | 14.8.93 | 17,691.00 | 665.08 |
| 3 | 15.11.93 | 28,050.00 | 1054.51 |
| 4 | 14.3.94 | 40,883.00 | 1536.95 |
| 5 | 14.4.94 | 44,441.00 | 1670.71 |
| 6 | 28.4.94 | 47,778.00 | 1796.17 |
| 7 | 26.5.94 | 52,600.00 | 1977.44 |
| 8 | 8.9.94 | 58,614.00 | 2203.53 |
| 9 | 6.10.94 | 55,358.00 | 2081.13 |
| 10 | 10.11.94 | 72,867.00 | 2739.36 |
| 11 | 1.12.94 | 78,955.00 | 2968.23 |
| 12 | 29.12.94 | 97,897.00 | 3680.34 |
| 13 | 2.2.95 | 129,165.00 | 4855.83 |
| 14 | 2.3.95 | 151,375.00 | 5690.79 |
| 15 | 30.3.95 | 160,817.00 | 6045.75 |
| 16 | 27.4.95 | 159,780.00 | 6006.77 |
| 17 | 1.6.95 | 167,590.00 | 6300.38 |
| 18 | 29.6.95 | 170,721.00 | 6418.08 |
| 19 | 27.7.95 | 175,499.00 | 6597.71 |
| 20 | 31.8.95 | 173,676.00 | 6529.17 |
| 22 | 28.9.95 | 217,542.00 | 8178.27 |
| 23 | 26.10.95 | 243,479.00 | 9153.35 |
| 24 | 30.11.95 | 222,417.00 | 8361.54 |
| 25 | 28.12.95 | 265,716.00 | 9989.32 |
| 26 | 1.2.96 | 287,472.55 | 10,807.24 |
| 27 | 5.3.96 | 297,958.00 | 11,201.43 |
| 28 | 5.4.96 | 304,033.44 | 11,429.83 |
| 29 | 8.5.96 | 305,809.55 | 11,496.60 |
| 30 | 5.6.96 | 302,381.69 | 11,367.73 |
| 31 | 3.7.96 | 306,065.21 | 11,506.21 |
| 32 | 3.8.96 | 308,963.42 | 11,615.17 |
| 33 | 7.9.96 | 288,835.07 | 10,858.46 |
| 34 | 1.10.96 | 278,235.35 | 10,459.98 |
| 35 | 5.11.96 | 287,094.77 | 10,793.04 |
| 36 | 4.12.96 | 298,024.76 | 11,203.94 |
| 37 | 3.1.97 | 314,287.16 | 11,815.31 |
| 38 | 4.2.97 | 334,738.24 | 12,584.14 |
| 39 | 4.1.98 | 345.72 | 12.997 |
| 40 | 3.1.99 | 622.30 | 23.395 |
| 41 | 5.1.00 | 851.32 | 32.004 |
| 42 | 3.1.01 | 949.21 | 35.684 |
| 43 | 2.7.01 | 1072.61 | 40.323 |
| 44 | 3.1.02 | 1125,76 | 43,321 |
| 45 | 2.7.02 | 1247.77 | 46.908 |
| 46 | 3.1.03 | 1295.75 | 48.712 |
| 47 | 1.7.03 | 1398.11 | 52.558 |

