НОУ ИНТУИТ | Введение в информатику. Лекция 5: Высказывания и предикаты

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 09.11.2006 | Уровень: для всех | Доступ: свободно

|

Вам нравится? Нравится 123 студентам

| Поделиться |

Поддержать

| Скачать электронную книгу

Аннотация: Рассматриваются основные понятия и сведения алгебры высказываний и предикатов – высказывания, предикаты, аксиомы, логические выражения и функции, эквивалентные выражения и приведение к эквивалентному выражению, другие сопутствующие понятия и факты логики, а также инфологические задачи.

Ключевые слова: информатика, алгебра, ПО, аксиома, операции, сигнатура, носитель, высказывательная форма, единица, высказывание, истина, ложь, true, переменная, значение, предикат, выражение, логическая функция, аргумент, множества, дизъюнкция, конъюнкция, таблица, функция, операция импликации, отрицание, тавтология, упрощения логического выражения, эквивалентное выражение, логическое выражение, равенство, инфологическая задача, логический вывод, умозаключение, алгебра логики, вывод, доказательство

Информатика, как было рассмотрено выше, изучает знаковые (алфавитные) системы. Алгебра – наиболее адекватный математический аппарат описания действий в них, поэтому алгебраический аппарат наилучшим образом подходит для описания информационных систем общей природы, отвлеченно от их предметной направленности. Информационные процессы хорошо формализуются с помощью различных алгебраических структур.

Алгеброй A называется некоторая совокупность определенных элементов X, с заданными над ними определенными операциями f (часто определяемые по сходству с операциями сложения и умножения чисел), которые удовлетворяют определенным свойствам – аксиомам алгебры.

Операция f называется n-местной, если она связывает n операндов (объектов – участников этой операции).

Совокупность операций алгебры A называется ее сигнатурой, а совокупность элементов алгебры – носителем алгебры.

Утверждение ( высказывательная форма ) – основная единица, неделимая с точки зрения отражения смысла информации (семантики).

Высказывание – некоторое повествовательное утверждение, про которое можно однозначно сказать ("сразу посмотрев на него"), истинно оно или ложно. Эти два значения всевозможных высказываний обозначаются "истина" и "ложь", "true" и "fаlse" или "1" и "0".

Переменная, значениями которой могут быть лишь значения "1" или "0", называется логической переменной или булевой переменной.

Пример. Рассмотрим словосочетания:

Москва – столица США.
Житель города Москва.
5 – 7 + 8.
5 – 9 + 28 = 4.
В пятую неделю зимы было очень холодно.
В Антарктиде живут тигры.

Высказывание должно быть однозначно истинным или однозначно ложным, поэтому высказываниями являются только утверждения 1), 4), 6).

Пример. Не является высказыванием и "парадокс лжеца" (Эвбулид, учитель Демосфена, около 350 лет до н.э.): "То, что я сейчас утверждаю, – ложно", ибо если оно истинно – то оно ложно, а если допустить, что оно ложно, то оно истинно. Это неопределенная высказывательная форма. Аналогичный пример принадлежит известному математику, логику Гёделю (1931 г.): "То, что утверждается в этом предложении, не может быть доказано". Если его можно опровергнуть, то его нельзя доказать, а если его нельзя опровергнуть, то его можно доказать. Предложения такого рода не могут быть доказаны или опровергнуты в пределах того языка (той теории, алгебры ), с помощью которой они сформулированы. Известны многие подобные парадоксы.

Рассматривая высказывания, мы не обращаем внимания на их внутреннюю структуру и можем разлагать их на структурные части, равно как и объединять их.

Пример. Построим из ниже заданных простых высказываний составные, сложные высказывания, принимающие значение "истина", "ложь":

"Зима – холодное время года".
"Пальто – теплая одежда".
"Камин – источник тепла".

Истинным будет, например, сложное высказывание: "Зима – холодное время года и зимой носят пальто", а ложным будет, например, высказывание: "Некоторые ходят в пальто, поэтому на улице зима". Придумайте другие примеры.

Предикат – высказывательная форма с логическими переменными (множество значений этих переменных вполне определено), имеющая смысл при любых допустимых значениях этих переменных. Количество переменных в записи предиката называется его местностью.

Простые высказывания или предикаты не зависят от других высказываний или предикатов ("не разбиваемы на более простые"), а сложные – зависят хотя бы от двух простых.

Пример. Выражение "х = у" – предикат, "х > 5" – предикат, а "7 > 5" – высказывание. Утверждение "Хорошо" не является высказыванием, утверждение "Оценка студента А по информатике – хорошая" – простое высказывание, утверждение "Вчера была ясная погода, я был вчера на рыбалке" – сложное высказывание, состоящее из двух простых.

Логической (булевой) функцией f(х) называется некоторая функциональная зависимость, в которой аргумент х – логическая переменная с заданным множеством изменений аргумента, а значения функции f(x) берутся из двухэлементного множества R(f) = {1,0}.

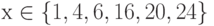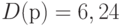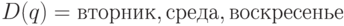Пример. Заданы предикаты вида р = "число х делится нацело на 3" и q = "у – день недели". Найдем множество истинности предикатов р и q, если $х \in \{1, 4, 6, 16, 20, 24\}$ , $у \in \{первый, вторник, среда, 1999, зима, выходной, праздник, воскресенье\}$ . Получаем, что D(р)={6, 24} , D(q) = {вторник, среда, воскресенье} .

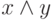Множество логических переменных $х,y \in Х$ с определенными над ним операциями: $\overline{x}$ – отрицания или инверсии, $x \lor y$ – логического сложения или дизъюнкции, $x \land y$ – логического умножения или конъюнкции называется алгеброй предикатов (и высказываний ) , если эти операции удовлетворяют следующим аксиомам:

Аксиома двойного отрицания:

$\overline{\overline{x}}=x$
Аксиомы переместительности операндов (относительно операций дизъюнкции и конъюнкции ):

$x \land y = y\land x, x \lor y = y \lor x$
Аксиомы переместительности операций дизъюнкции и конъюнкции (относительно операндов):

$(x \land y) \land z = x \land (y \land z), (x \lor y) \lor z = x \lor (y \lor z)$
Аксиомы одинаковых операндов:

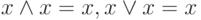
$x\land x = x, x \lor x = x$
Аксиомы поглощения (множителем — множителя-суммы или слагаемым — слагаемого-произведения):

$x \land (x \lor y) = x, x \lor (x \land y) = x$
Аксиомы распределения операции ( дизъюнкции относительно конъюнкции и наоборот):

$x \land (y \lor z) = (x \land y) \lor (x \land z), x \lor (y \land z) = (x \lor y) \land (x \lor z)$
Аксиомы де Моргана (перенесения бинарной операции на операнды):

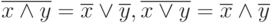
$\overline{x\land y} = \overline{x}\lor\overline{y}, \overline{x\lor y}=\overline{x}\land\overline{y}$
Аксиомы нейтральности (взаимноинверсных множителей или слагаемых):

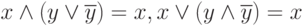
$x\land(y\lor\overline{y})=x, x\lor(y\land\overline{y})=x$
Аксиома существования единицы ( истина, true, 1) и нуля ( ложь, false, 0), причем,

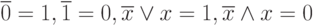
$\overline{0}=1, \overline{1}=0, \overline{x}\lor x=1, \overline{x}\land x = 0$