Арифметико-логическое устройство
Классическая ЭВМ состоит из трех основных устройств: арифметико-логического устройства, устройства управления и запоминающего устройства. Рассмотрим особенности организации этих устройств. Прежде всего, рассмотрим структуру арифметико-логического устройства.
В современных ЭВМ арифметико-логическое устройство не является самостоятельным схемотехническим блоком. Оно входит в состав микропроцессора, на котором строится компьютер. Однако знание структуры и принципов работы АЛУ весьма важно для понимания работы компьютера в целом. Для лучшего понимания этих вопросов проведем синтез арифметического устройства, предназначенного для выполнения только одной операции – умножения чисел с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя [13] . В ходе этого процесса также обратим внимание на особенности использования рассмотренных выше основных схемотехнических элементов ЭВМ.
Синтез АЛУ проходит в несколько этапов. Сначала необходимо выбрать метод, по которому предполагается выполнение операции, и составить алгоритм соответствующих действий. Исходя из алгоритма и формата исходных данных, следует определить набор составляющих АЛУ элементов. Затем требуется определить связи между элементами, установить порядок функционирования устройства и временную диаграмму управляющих сигналов, которые должны быть поданы на АЛУ от устройства управления.
Пусть операнды имеют вид:
[X]пк = x0x1x2…xn [Y]пк = y0y1y2…yn
где x0, y0 – знаковые разряды.
Операция умножения чисел с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя выполняется по следующей формуле:
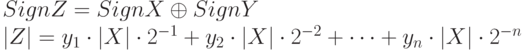
![[X]_{пк} = 0.1101; Sign X = 0
\\
[Y]_{пк} = 1.1011; Sign Y = 1
\\
Sign Z = 0 \oplus 1 = 1
\\
|X| = 0. 1 1 0 1
\\
|Y| = 0. 1 0 1 1
\\
y_{1}y_{2}y_{3}y_{4}
\\
+0.00000000 |Z| = 0
\\
y_{1} = 1 0.01101000 1 \cdot |X| \cdot 2^{-1}
\\
+ \ovwerline {0.01101000} |Z| = |Z| + |X| \cdot 2^{-1}
\\
y_{2} = 0 0.00000000 0 \cdot |X| \cdot 2^{-2}
\\
+ \overline {0.01101000} |Z| = |Z| + 0
\\
y_{3} = 1 0.00011010 1 \cdot |X| \cdot 2^{-3}
\\
+ \overline {0.10000010} |Z| = |Z| + |X| \cdot 2^{-3}
\\
y_{4} = 1 0.00001101 1 \cdot |X| \cdot 2^{-4}
\\
\overline {0.10001111} |Z| = |Z| + |X| \cdot 2^{-4}](/sites/default/files/tex_cache/7af37921efed33c4bbe7f79df3e492e3.png)
Алгоритм вычислений представлен на рис. 3.1
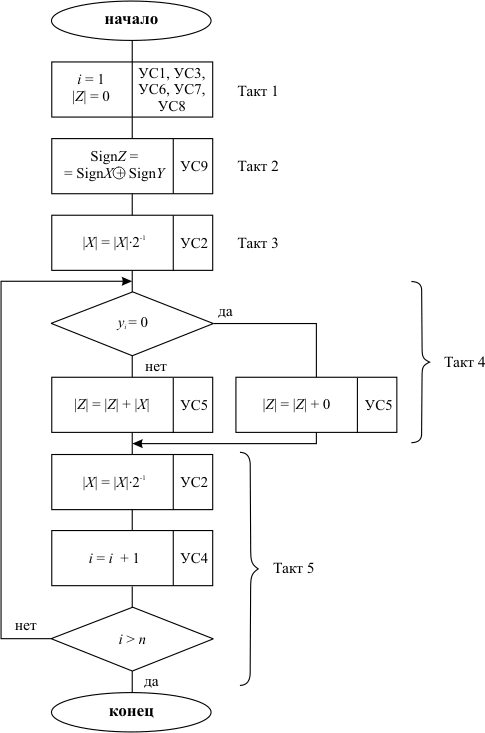
Рис. 3.1. Алгоритм операции умножения чисел с фиксированной запятой, заданных в прямом коде, со старших разрядов множителя
Каждой переменной, представленной в алгоритме, в схеме должен соответствовать элемент хранения. Разрядность модуля произведения равна сумме разрядностей сомножителей. Умножение двоичного числа на 2-i обеспечивается сдвигом этого числа вправо на соответствующее количество разрядов. Переход к анализу очередного разряда множителя ( i = i + 1 ) может быть обеспечен сдвигом регистра множителя на один разряд в сторону старших разрядов.
Исходя из этого, определим состав оборудования, необходимого для реализации АЛУ заданного типа для n = 4 ( таблица 3.1).
Структурная схема устройства представлена на рис. 3.2.

