|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистика нечисловых данных
Случайные множества. Будем рассматривать случайные подмножества некоторого множества 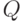 . Если
. Если 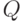 состоит из конечного числа элементов, то считаем, что случайное подмножество
состоит из конечного числа элементов, то считаем, что случайное подмножество 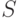 - это случайный элемент со значениями в
- это случайный элемент со значениями в  - множестве всех подмножеств множества
- множестве всех подмножеств множества 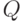 , состоящем из
, состоящем из  элементов. Чтобы удовлетворить математиков, считаем, что все подмножества
элементов. Чтобы удовлетворить математиков, считаем, что все подмножества 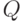 измеримы. Тогда распределение случайного подмножества
измеримы. Тогда распределение случайного подмножества 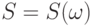 множества
множества  - это
- это
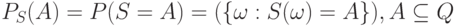 |
( 6) |
В формуле (6) предполагается, что  где
где  - вероятностное пространство (здесь
- вероятностное пространство (здесь  - пространство элементарных событий,
- пространство элементарных событий,  -алгебра случайных событий,
-алгебра случайных событий,  -вероятностная мера на
-вероятностная мера на 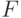 ), на котором определен случайный элемент
), на котором определен случайный элемент 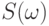 .Через распределение
.Через распределение  выражаются вероятности различных событий, связанных с
выражаются вероятности различных событий, связанных с 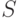 . Так ,чтобы найти вероятность накрытия фиксированного элемента
. Так ,чтобы найти вероятность накрытия фиксированного элемента 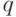 случайным множеством
случайным множеством 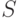 , достаточно вычислить
, достаточно вычислить

где суммирование идет по всем подмножествам  множества
множества 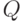 , содержащим
, содержащим 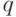 . Пусть
. Пусть  . Рассмотрим случайные величины, определяемые по случайному множеству S следующим образом
. Рассмотрим случайные величины, определяемые по случайному множеству S следующим образом

Определение 3. Случайное множество 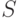 называется случайным множеством с независимыми элементами, если случайные величины
называется случайным множеством с независимыми элементами, если случайные величины  независимы (в совокупности).
независимы (в совокупности).
Последовательность случайных величин  -бернуллиевский вектор с
-бернуллиевский вектор с  и
и  Из последней формулы подпункта "Дихотомические данные" следует, что распределение случайного множества с независимыми элементами задается формулой
Из последней формулы подпункта "Дихотомические данные" следует, что распределение случайного множества с независимыми элементами задается формулой

т.е. такие распределения образуют  - мерное параметрическое семейство, входящее в
- мерное параметрическое семейство, входящее в  - одномерное семейство всех распределений случайных подмножеств множества
- одномерное семейство всех распределений случайных подмножеств множества 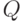 .
.
При исследовании случайных подмножеств произвольного множества 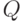 будем рассматривать их как случайные величины со значениями в некотором пространстве подмножеств множества
будем рассматривать их как случайные величины со значениями в некотором пространстве подмножеств множества  , например, в пространстве замкнутых подмножеств
, например, в пространстве замкнутых подмножеств  множества
множества 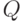 . Представляющими интерес лишь для математиков способами введения измеримой структуры в
. Представляющими интерес лишь для математиков способами введения измеримой структуры в  интересоваться не будем. Отсутствие специального интереса к проблеме измеримости связано с тем, что при эконометрическом моделировании и обработке на ЭВМ все случайные подмножества рассматриваются как конечные (т.е. подмножества конечного множества).
интересоваться не будем. Отсутствие специального интереса к проблеме измеримости связано с тем, что при эконометрическом моделировании и обработке на ЭВМ все случайные подмножества рассматриваются как конечные (т.е. подмножества конечного множества).
Случайные множества находят разнообразные применения в многообразных проблемах эконометрики и математической экономики, в том числе в задачах управлении запасами и ресурсами (см. об этом главу 5 в монографии [3]), в задачах менеджмента и маркетинга, в экспертных оценках, в частности, при анализе мнений голосующих или опрашиваемых, каждый из которых отмечает несколько пунктов из списка и т.д. Кроме того, случайные множества применяются в гранулометрии, при изучении пористых сред и объектов сложной природы в таких областях, как металлография, петрография, биология, в частности, математическая морфология, в изучении структуры веществ и материалов, в исследовании процессов распространения, в частности, просачивания, распространения пожаров, экологических загрязнений, при районировании, в том числе в изучении областей поражения, в частности, поражения металла коррозией и сердечной мышцы при инфаркте миокарда, и т.д., и т.п. Можно вспомнить о компьютерной томографии, о наглядном представлении сложной информации на экране компьютера, об изучении распространения рекламной информации, о картах Кохонена (популярный метод представления информации при применении нейросетей) и т.д.
Ранговые методы. Ранее установлено, что любой адекватный алгоритм в порядковой шкале является функцией от некоторой матрицы  . Пусть никакие два из результатов наблюдений
. Пусть никакие два из результатов наблюдений 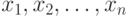 не совпадают, а
не совпадают, а 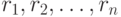 - их ранги. Тогда элементы матрицы C и ранги результатов наблюдений связаны взаимно однозначным соответствием:
- их ранги. Тогда элементы матрицы C и ранги результатов наблюдений связаны взаимно однозначным соответствием:

а  через ранги выражаются так:
через ранги выражаются так:  , если
, если  и
и  в противном случае.
в противном случае.
Сказанное означает, что при обработке данных, измеренных в порядковой шкале, могут применяться только ранговые статистические методы. Отметим, что часто используемое в непараметрической статистике преобразование  (здесь
(здесь  - непрерывная функция распределения случайной величины
- непрерывная функция распределения случайной величины  , причем
, причем  предполагается произвольной) фактически означает переход к порядковой шкале, поскольку статистические выводы при этом инвариантны относительно допустимых преобразований в порядковой шкале.
предполагается произвольной) фактически означает переход к порядковой шкале, поскольку статистические выводы при этом инвариантны относительно допустимых преобразований в порядковой шкале.
Разумеется, ранговые статистические методы могут применяться не только при обработке данных, измеренных в порядковой шкале. Так, для проверки независимости двух количественных признаков в случае, когда нет уверенности в нормальности соответствующего двумерного распределения, целесообразно пользоваться коэффициентами ранговой корреляции Кендалла или Спирмена.
Как было подробно обосновано в "Статистический анализ числовых величин (непараметрическая статистика)" и "Многомерный статистический анализ" , в настоящее время с помощью непараметрических и прежде всего ранговых методов можно решать все те задачи эконометрики и прикладной статистики, что и с помощью параметрических методов, в частности, основанных на предположении нормальности. Однако параметрические методы вошли в массовое сознание исследователей и инженеров и мешают широкому внедрению более обоснованной и прогрессивной ранговой статистики. Так, при проверке однородности двух выборок вместо критерия Стъюдента целесообразно использовать ранговые методы, но пока это делается редко.
Объекты общей природы. Вероятностная модель объекта нечисловой природы в общем случае- случайный элемент со значениями в пространстве произвольного вида, а модель выборки таких объектов - совокупность независимых одинаково распределенных случайных элементов. Именно такая модель была использована для обработки наблюдений, каждое из которых - нечеткое множество [10].
Из-за имеющего разнобоя в терминологии приведем математические определения из справочника по теории вероятностей академика РАН Ю.В Прохорова и проф. Ю.А. Розанова [25].
Пусть  -некоторое измеримое пространство;
-некоторое измеримое пространство; 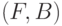 -измеримая функция
-измеримая функция 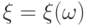 на пространстве элементарных событий
на пространстве элементарных событий  (где
(где  - вероятностная мера на
- вероятностная мера на  -алгебре
-алгебре  - измеримых подмножеств
- измеримых подмножеств  , называемых событиями) со значениями в
, называемых событиями) со значениями в  называется случайной величиной (чаще этот математический объект называют случайным элементом, оставляя термин "случайная величина" за частным случаем, когда
называется случайной величиной (чаще этот математический объект называют случайным элементом, оставляя термин "случайная величина" за частным случаем, когда 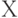 - числовая прямая) в фазовом пространстве
- числовая прямая) в фазовом пространстве  . Распределением вероятностей этой случайной величины
. Распределением вероятностей этой случайной величины  называется функция
называется функция 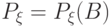 на
на  -алгебре фазового пространства, определенная как
-алгебре фазового пространства, определенная как
 |
( 7) |
(распределение вероятностей 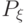 представляет собой вероятностную меру в фазовом пространстве
представляет собой вероятностную меру в фазовом пространстве  ) [25, с. 132].
) [25, с. 132].
Пусть 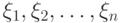 - случайные величины на пространстве случайных событий
- случайные величины на пространстве случайных событий  в соответствующих фазовых пространствах
в соответствующих фазовых пространствах  . Совместным распределением вероятностей этих величин называется функция
. Совместным распределением вероятностей этих величин называется функция  , определенная на множествах
, определенная на множествах 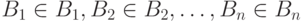 как
как
 |
( 8) |
Распределение вероятностей  как функция на полукольце множеств вида
как функция на полукольце множеств вида  в произведении пространств
в произведении пространств 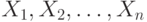 представляет собой функцию распределения. Случайные величины
представляет собой функцию распределения. Случайные величины 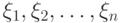 называются независимыми, если при любых
называются независимыми, если при любых  (см. [25, с.133])
(см. [25, с.133])
 |
( 9) |
Предположим, что совместное распределение вероятностей  случайных величин
случайных величин  и
и  абсолютно непрерывно относительно некоторой меры
абсолютно непрерывно относительно некоторой меры  на произведении пространств
на произведении пространств  , являющейся произведением мер
, являющейся произведением мер  и
и 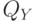 , т.е.:
, т.е.:
 |
( 10) |
для любых  и
и  , где
, где 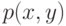 - соответствующая плотность распределения вероятностей [25, с.145].
- соответствующая плотность распределения вероятностей [25, с.145].
В формуле (10) предполагается, что 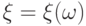 и
и 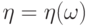 - случайные величины на одном и том же пространстве элементарных событий
- случайные величины на одном и том же пространстве элементарных событий  со значениями в фазовых пространствах
со значениями в фазовых пространствах  и
и  . Существование плотности
. Существование плотности 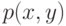 вытекает из абсолютной непрерывности
вытекает из абсолютной непрерывности  относительно
относительно  в соответствии с теоремой Радона - Никодима.
в соответствии с теоремой Радона - Никодима.
Условное распределение вероятностей  может быть выбрано одинаковым для всех
может быть выбрано одинаковым для всех  при которых случайная величина
при которых случайная величина 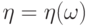 сохраняет одно и то же значение:
сохраняет одно и то же значение: 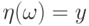 При почти каждом
При почти каждом  (относительно распределения
(относительно распределения 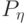 в фазовом пространстве
в фазовом пространстве  ) условное распределение вероятностей
) условное распределение вероятностей  где
где  и
и  будет абсолютно непрерывно относительно меры
будет абсолютно непрерывно относительно меры 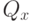 :
:

Причем соответствующая плотность условного распределения вероятностей будет иметь вид:
 |
( 11) |
При построении вероятностных моделей реальных явлений важны вероятностные пространства из конечного числа элементарных событий. Для них перечисленные выше общие понятия становятся более прозрачными, в частности, снимаются вопросы измеримости (все подмножества конечного множества обычно считаются измеримыми). Вместо плотностей и условных плотностей рассматриваются вероятности и условные вероятности. Отметим, что вероятности можно рассматривать как плотности относительно меры, приписывающей каждому элементу пространства элементарных событий вес 1, т.е. считающей меры 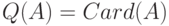 (мера каждого множества равна числу его элементов). В целом ясно, что определения основных понятий теории вероятностей в общем случае практически не отличаются от таковых в элементарных курсах, во всяком случае с идейной точки зрения.
(мера каждого множества равна числу его элементов). В целом ясно, что определения основных понятий теории вероятностей в общем случае практически не отличаются от таковых в элементарных курсах, во всяком случае с идейной точки зрения.
За последние двадцать лет в эконометрике и прикладной математической статистике сформировалась новая область - статистика нечисловых данных, она же - статистика объектов нечисловой природы. К настоящему времени она развита не менее, чем ранее выделенные статистика случайных величин, многомерный статистический анализ, статистика временных рядов и случайных процессов. Краткая сводка основных постановок и результатов математической статистики в пространствах нечисловой природы даны ниже в настоящей лекции. Теория, построенная для результатов наблюдений, лежащих в пространствах общей природы, является центральным стержнем в статистике нечисловой природы. В ее рамках удалось разработать и изучить методы оценивания параметров и характеристик, проверки гипотез (в частности, с помощью статистик интегрального типа), параметрической и непараметрической регрессии (восстановления зависимостей), непараметрического оценивания плотности, дискриминантного и кластерного анализов и т.д.
Вероятностно-статистические методы, развитые для результатов наблюдений из пространств произвольного вида, позволяют единообразно проводить анализ данных из любого конкретного пространства. Так, в монографии [3] они применены к конечным случайным множествам, в работе [10] - к нечетким множествам. С их помощью установлено поведение обобщенного мнения экспертной комиссии (медианы Кемени) при увеличении числа экспертов, когда ответы экспертов лежат в том или ином пространстве бинарных отношений. В пункте методы распознавания образов, основанные на непараметрических оценках плотности распределения вероятностей в пространстве общей природы, применены для разработки алгоритма диагностики в пространстве разнотипных данных (часть координат вектора измерена по количественным шкалам, часть - по качественным - см. "Основы теории измерений" ).
