Нечеткие и случайные множества

В "Статистика нечисловых данных" рассматривались такие виды объектов нечисловой природы, как нечеткие и случайные множества. Цель настоящего приложения - глубже изучить свойства нечетких множеств и показать, что теория нечетких множеств в определенном смысле сводится к теории случайных множеств. Для достижения поставленной цели формулируется и доказывается цепь теорем.

В дальнейшем считается, что все рассматриваемые нечеткие множества являются подмножествами одного и того же множества .

П2-1. Законы де Моргана для нечетких множеств

Как известно, законами же Моргана называются следующие тождества алгебры множеств

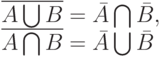( 1)

Теорема 1. Для нечетких множеств справедливы тождества

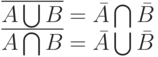( 2)

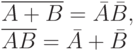( 3)

Доказательство теоремы 1 состоит в непосредственной проверке справедливости соотношений (2) и (3) путем вычисления значений функций принадлежности участвующих в этих соотношениях нечетких множеств на основе определений, данных в "Статистика нечисловых данных" .

Тождества (2) и (3) назовем законами де Моргана для нечетких множеств. В отличие от классического случая соотношений (1), они состоят из четырех тождеств, одна пара которых относится к операциям объединения и пересечения, а вторая - к операциям произведения и суммы. Как и соотношение (1) в алгебре множеств, законы де Моргана в алгебре нечетких множеств позволяют преобразовывать выражения и формулы, в состав которых входят операции отрицания.

П2-2. Дистрибутивный закон для нечетких множеств

Некоторые свойства операций над множествами не выполнены для нечетких множеств. Так, 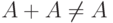за исключением случая, когда - "четкое" множество (т.е. функция принадлежности принимает только значения 0 и 1).

Верен ли дистрибутивный закон для нечетких множеств? В литературе иногда расплывчато утверждается, что "не всегда". Внесем полную ясность.

Теорема 2. Для любых нечетких множеств 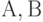и

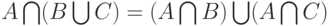( 4)

В то же время равенство

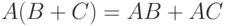( 5)

справедливо тогда и только тогда, когда при всех

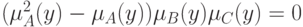
Доказательство. Фиксируем произвольный элемент . Для сокращения записи обозначим 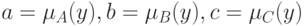. Для доказательства тождества (4) необходимо показать, что

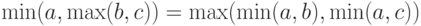( 6)

Рассмотрим различные упорядочения трех чисел 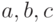. Пусть сначала Тогда левая часть соотношения (6) есть 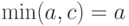а правая т.е. равенство (6) справедливо.

Пусть Тогда в соотношении (6) слева стоит 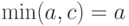а справа 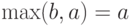т.е. соотношение (6) опять является равенством.

Если то в соотношении (6) слева стоит 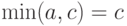а справа 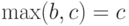т.е. обе части снова совпадают.

Три остальные упорядочения чисел 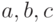разбирать нет необходимости, поскольку в соотношение (6) числа и входят симметрично. Тождество (4) доказано.

Второе утверждение теоремы 2 вытекает из того, что в соответствии с определениями операций над нечеткими множествами (см. "Статистика нечисловых данных" )

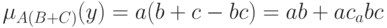
и

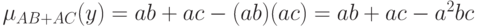
Эти два выражения совпадают тогда и только тогда, когда, когда что и требовалось доказать.

Определение 1. Носителем нечеткого множества называется совокупность всех точек 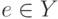, для которых

Следствие теоремы 2. Если носители нечетких множеств и совпадают с 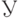, то равенство (5) имеет место тогда и только тогда, когда А - "четкое" (т.е. обычное, классическое, не нечеткое) множество.

Доказательство. По условию 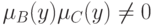при всех . Тогда из теоремы 2 следует, что 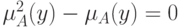т.е. или 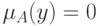, что и означает, что - четкое множество.

П2-3. Нечеткие множества как проекции случайных множеств

С самого начала появления современной теории нечеткости в 1960-е годы началось обсуждение ее взаимоотношений с теорией вероятностей. Дело в том, что функция принадлежности нечеткого множества напоминает распределение вероятностей. Отличие только в том, что сумма вероятностей по всем возможным значениям случайной величины (или интеграл, если множество возможных значений несчетно) всегда равна 1, а сумма значений функции принадлежности (в непрерывном случае - интеграл от функции принадлежности) может быть любым неотрицательным числом. Возникает искушение пронормировать функцию принадлежности, т.е. разделить все ее значения на 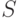(при 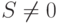), чтобы свести ее к распределению вероятностей (или к плотности вероятности). Однако специалисты по нечеткости справедливо возражают против такого "примитивного сведения", поскольку оно проводится отдельно для каждой размытости (нечеткого множества), и определения обычных операций над нечеткими множествами с ним согла совать нельзя. Последнее утверждение означает следующее. Пусть указанным образом преобразованы функции принадлежности нечетких множеств и . Как при этом преобразуются функции принадлежности 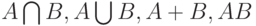? Установить это невозможно в принципе. Последнее утверждение становится совершенно ясным после рассмотрения нескольких примеров пар нечетких множеств с одними и теми же суммами значений функций принадлежности, но различными результатами теоретико-множественных операций над ними, причем и суммы значений соответствующих функций принадлежности для этих результатов теоретико-множественных операций, например, для пересечений множеств, также различны.

В работах по нечетким множествам довольно часто утверждается, что теория нечеткости является самостоятельным разделом прикладной математики и не имеет отношения к теории вероятностей (см., например, обзор литературы в монографиях [1],[2]). Авторы, сравнивавшие теорию нечеткости и теорию вероятностей, обычно подчеркивали различие между этими областями теоретических и прикладных исследований. Обычно сравнивают аксиоматику и сравнивают области приложений. Надо сразу отметить, что аргументы при втором типе сравнений не имеют доказательной силы, поскольку по поводу границ применимости даже такой давно выделившейся научной области, как вероятностно-статистические методы, имеются различные мнения. Напомним, что итог рассуждений одного из наиболее известных французских математиков Анри Лебега по поводу границ применимости арифметики таков: "Арифметика применима тогда, когда она применима" (см. его монографию [3, с.21-22]).

При сравнении различных аксиоматик теории нечеткости и теории вероятностей нетрудно увидеть, что списки аксиом различаются. Из этого, однако, отнюдь не следует, что между указанными теориями нельзя установить связь, типа известного сведения евклидовой геометрии на плоскости к арифметике (точнее к теории числовой системы - см., например, монографию [4]). Напомним, что эти две аксиоматики - евклидовой геометрии и арифметики - на первый взгляд весьма сильно различаются.

Можно понять желание энтузиастов нового направления подчеркнуть принципиальную новизну своего научного аппарата. Однако не менее важно установить связи нового подхода с ранее известными.

Как оказалось, теория нечетких множеств тесно связана с теорией случайных множеств. Еще в 1974 г. в работе [5] было показано, что нечеткие множества естественно рассматривать как "проекции" случайных множеств. Рассмотрим этот метод сведения теории нечетких множеств к теории случайных множеств.

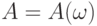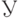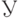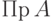Определение 2. Пусть - случайное подмножество конечного множества . Нечеткое множество , определенное на , называется проекцией и обозначается , если

( 7)

при всех

Очевидно, каждому случайному множеству можно поставить в соответствие с помощью формулы (7) нечеткое множество 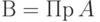. Оказывается, верно и обратное.

Теорема 3. Для любого нечеткого подмножества конечного множества 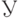существует случайное подмножество множества 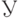такое, что .

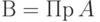Доказательство. Достаточно задать распределение случайного множества . Пусть 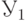- носитель В (см. определение 1 выше). Без ограничения общности можно считать, что 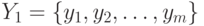при некотором и элементы 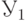занумерованы в таком порядке, что

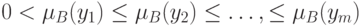
Введем множества

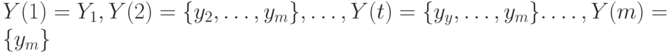
Положим

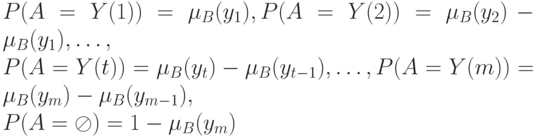
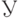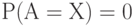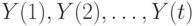Для всех остальных подмножеств множества положим . Поскольку элемент входит во множества и не входит во множества 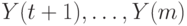, то из приведенных выше формул следует, что 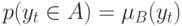Если 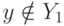то, очевидно, 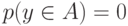Теорема 3 доказана.

Распределение случайного множества с независимыми элементами, как следует из рассмотрений "Статистика нечисловых данных" , полностью определяется его проекцией. Для конечного случайного множества общего вида это не так. Для уточнения сказанного понадобится следующая теорема.

Теорема 4. Для случайного подмножества множества 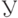из конечного числа элементов наборы чисел 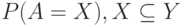и 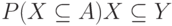выражаются один через другой.

Доказательство. Второй набор выражается через первый следующим образом:

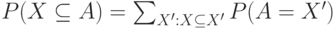
Элементы первого набора выразить через второй можно с помощью формулы включений и исключений из формальной логики, в соответствии с которой 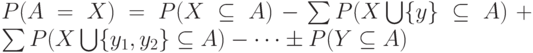В этой формуле в первой сумме пробегает все элементы множества , во второй сумме переменные суммирования 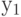и 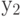не совпадают и также пробегают это множество, и т.д. Ссылка на формулу включений и исключений завершает доказательство теоремы 4.

В соответствии с теоремой 4 случайное множество можно характеризовать не только распределением, но и набором чисел 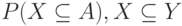. В этом наборе 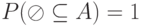а других связей типа равенств нет. В этот набор входят числа 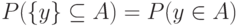следовательно, фиксация проекции случайного множества эквивалентна фиксации 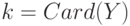параметров из 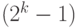параметров, задающих распределение случайного множества в общем случае.

Будет полезна следующая теорема.

Теорема 5. Если 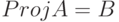, то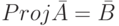

Для доказательства достаточно воспользоваться тождеством из теории случайных множеств 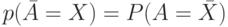формулой для вероятности накрытия из "Статистика нечисловых данных" , определением отрицания нечеткого множества и тем, что сумма всех равна 1.