|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Статистический анализ числовых величин (непараметрическая статистика)
Критерий Крамера-Уэлча равенства математических ожиданий. Вместо критерия Стьюдента предлагаем для проверки H'0 использовать критерий Крамера-Уэлча [12], основанный на статистике
 |
( 6) |
Критерий Крамера-Уэлча имеет прозрачный смысл - разность выборочных средних арифметических для двух выборок делится на естественную оценку среднего квадратического отклонения этой разности. Естественность указанной оценки состоит в том, что неизвестные статистику дисперсии заменены их выборочными оценками. Из многомерной центральной предельной теоремы и из теорем о наследовании сходимости [11] вытекает, что при росте объемов выборок распределение статистики Т Крамера-Уэлча сходится к стандартному нормальному распределению с математическим ожиданием 0 и дисперсией 1. Итак, при справедливости  и больших объемах выборок распределение статистики
и больших объемах выборок распределение статистики  приближается с помощью стандартного нормального распределения
приближается с помощью стандартного нормального распределения 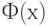 , из таблиц которого следует брать критические значения.
, из таблиц которого следует брать критические значения.
При 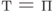 , как следует из формул (1) и (6),
, как следует из формул (1) и (6), 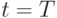 . При
. При 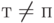 этого равенства нет. В частности, при
этого равенства нет. В частности, при 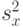 в (1) стоит множитель
в (1) стоит множитель  , а в (6)- множитель
, а в (6)- множитель  .
.
Если 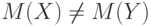 , то при больших объемах выборок
, то при больших объемах выборок
 |
( 7) |
где
![c_{mn}=\frac{\sqrt{mn}[M(X)-M(Y)]}{\sqrt{nD(X)+mD(Y)}}](/sites/default/files/tex_cache/a55a407e2fba12b769043f242b7b8d1f.png) |
( 8) |
При 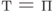 или
или 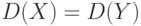 , согласно формулам (3) и (8),
, согласно формулам (3) и (8),  в остальных случаях равенства нет.
в остальных случаях равенства нет.
Из асимптотической нормальности статистики  , формул (7) и (8) следует, что правило принятия решения для критерия Крамера-Уэлча выглядит так:
, формул (7) и (8) следует, что правило принятия решения для критерия Крамера-Уэлча выглядит так:
- если
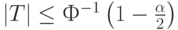 то гипотеза однородности (равенства) математических ожиданий принимается на уровне значимости
то гипотеза однородности (равенства) математических ожиданий принимается на уровне значимости 
- если же
 то гипотеза однородности (равенства) математических ожиданий отклоняется на уровне значимости
то гипотеза однородности (равенства) математических ожиданий отклоняется на уровне значимости  .
.
В эконометрике наиболее часто применяется уровень значимости 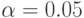 Тогда значение модуля статистики
Тогда значение модуля статистики  Крамера-Уэлча надо сравнивать с граничным значением
Крамера-Уэлча надо сравнивать с граничным значением 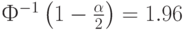 .
.
Из сказанного выше следует, что применение критерия Крамера-Уэлча не менее обосновано, чем применение критерия Стьюдента. Дополнительное преимущество - не требуется равенства дисперсий 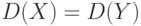 . Распределение статистики Т не является распределением Стьюдента, однако и распределение статистики
. Распределение статистики Т не является распределением Стьюдента, однако и распределение статистики  , как показано выше, не является таковым в реальных ситуациях.
, как показано выше, не является таковым в реальных ситуациях.
Распределение статистики  при объемах выборок
при объемах выборок 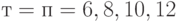 и различных функциях распределений выборок
и различных функциях распределений выборок  и
и 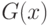 изучено нами совместно с Ю.Э. Камнем и Я.Э. Камнем методом статистических испытаний (Монте-Карло). Рассмотрены различные варианты функций распределения
изучено нами совместно с Ю.Э. Камнем и Я.Э. Камнем методом статистических испытаний (Монте-Карло). Рассмотрены различные варианты функций распределения  и
и 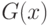 . Результаты показывают, что даже при таких небольших объемах выборок точность аппроксимации предельным стандартным нормальным распределением вполне удовлетворительна. Поэтому представляется целесообразным во всех тех случаях, когда в настоящее время используется критерий Стьюдента, заменить его на критерий Крамера-Уэлча. Конечно, такая замена потребует переделки ряда нормативно-технических и методических документов, исправления учебников и учебных пособий для вузов.
. Результаты показывают, что даже при таких небольших объемах выборок точность аппроксимации предельным стандартным нормальным распределением вполне удовлетворительна. Поэтому представляется целесообразным во всех тех случаях, когда в настоящее время используется критерий Стьюдента, заменить его на критерий Крамера-Уэлча. Конечно, такая замена потребует переделки ряда нормативно-технических и методических документов, исправления учебников и учебных пособий для вузов.
Пример. Пусть объем первой выборки 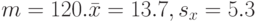 Для второй выборки
Для второй выборки 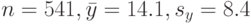 Вычислим величину статистики Крамера-Уэлча
Вычислим величину статистики Крамера-Уэлча
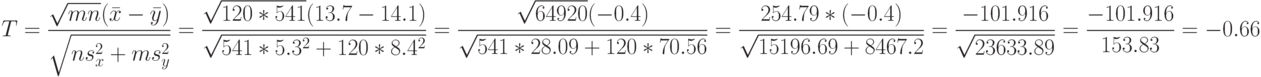
Поскольку полученное значение по абсолютной величине меньше 1,96, то гипотеза однородности математических ожиданий принимается на уровне значимости 0,05.
Непараметрические методы проверки однородности. В большинстве экономических и технико-экономических задач представляет интерес не проверка равенства математических ожиданий или иных характеристик распределения, а обнаружение различия генеральных совокупностей, из которых извлечены выборки, т.е. проверка гипотезы  . Методы проверки гипотезы
. Методы проверки гипотезы  позволяют обнаружить не только изменение математического ожидания, но и любые иные изменения функции распределения результатов наблюдений при переходе от одной выборки к другой (увеличение разброса, появление асимметрии и т. д.). Как установлено выше, методы, основанные на использовании статистик
позволяют обнаружить не только изменение математического ожидания, но и любые иные изменения функции распределения результатов наблюдений при переходе от одной выборки к другой (увеличение разброса, появление асимметрии и т. д.). Как установлено выше, методы, основанные на использовании статистик  Стьюдента и Т Крамера-Уэлча, не позволяют проверять гипотезу
Стьюдента и Т Крамера-Уэлча, не позволяют проверять гипотезу  Априорное предположение о принадлежности функций распределения
Априорное предположение о принадлежности функций распределения  и
и 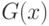 к какому-либо определенному параметрическому семейству (например, семействам нормальных, логарифмически нормальных, распределений Вейбулла-Гнеденко, гамма-распределений и др.), как показано выше, обычно нельзя достаточно надежно обосновать. Поэтому для проверки
к какому-либо определенному параметрическому семейству (например, семействам нормальных, логарифмически нормальных, распределений Вейбулла-Гнеденко, гамма-распределений и др.), как показано выше, обычно нельзя достаточно надежно обосновать. Поэтому для проверки  следует использовать методы, пригодные при любом виде
следует использовать методы, пригодные при любом виде  и
и 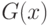 , т.е. непараметрические методы. (Термин "непараметрический метод" означает, что при использовании этого метода нет необходимости предполагать, что функции распределения результатов наблюдений принадлежат какому-либо определенному параметрическому семейству.)
, т.е. непараметрические методы. (Термин "непараметрический метод" означает, что при использовании этого метода нет необходимости предполагать, что функции распределения результатов наблюдений принадлежат какому-либо определенному параметрическому семейству.)
Для проверки гипотезы  разработано много непараметрических методов - критерии Смирнова, типа омега-квадрат (Лемана-Розенблатта), Вилкоксона (Манна-Уитни), Ван-дер-Вардена, Сэвиджа, хи-квадрат и др.. Распределения статистик всех этих критериев при справедливости
разработано много непараметрических методов - критерии Смирнова, типа омега-квадрат (Лемана-Розенблатта), Вилкоксона (Манна-Уитни), Ван-дер-Вардена, Сэвиджа, хи-квадрат и др.. Распределения статистик всех этих критериев при справедливости  не зависят от конкретного вида совпадающих функций распределения
не зависят от конкретного вида совпадающих функций распределения  . Следовательно, таблицами точных и предельных (при больших объемах выборок) распределений статистик этих критериев и их процентных точек можно пользоваться при любых непрерывных функциях распределения результатов наблюдений.
. Следовательно, таблицами точных и предельных (при больших объемах выборок) распределений статистик этих критериев и их процентных точек можно пользоваться при любых непрерывных функциях распределения результатов наблюдений.
Каким из непараметрических критериев пользоваться? Как известно [10], для выбора одного из нескольких критериев необходимо сравнить их мощности, определяемые видом альтернативных гипотез. Сравнению мощностей критериев посвящена обширная литература.
Хорошо изучены свойства критериев при альтернативной гипотезе сдвига
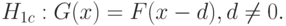
Критерии Вилкоксона, Ван-дер-Вардена и ряд других ориентированы для применения именно в этой ситуации. Если  раз измеряют характеристику одного объекта и
раз измеряют характеристику одного объекта и  раз - другого, а функция распределения погрешностей измерения произвольна, но не меняется при переходе от объекта к объекту (это более жесткое требование, чем условие равенства дисперсий), то рассмотрение гипотезы
раз - другого, а функция распределения погрешностей измерения произвольна, но не меняется при переходе от объекта к объекту (это более жесткое требование, чем условие равенства дисперсий), то рассмотрение гипотезы 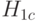 оправдано. Однако в большинстве экономических и технико-экономических исследований нет оснований считать, что функции распределения, соответствующие выборкам, различаются только сдвигом.
оправдано. Однако в большинстве экономических и технико-экономических исследований нет оснований считать, что функции распределения, соответствующие выборкам, различаются только сдвигом.
Какие гипотезы можно проверять с помощью двухвыборочного критерия Вилкоксона?
Покажем (и это - основной результат настоящего пункта), что двухвыборочный критерий Вилкоксона (в литературе его называют также критерием Манна-Уитни) предназначен для проверки гипотезы
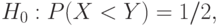
где  - случайная величина, распределенная как элементы первой выборки, а
- случайная величина, распределенная как элементы первой выборки, а 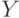 - второй.
- второй.
В описанной выше вероятностной модели двух независимых выборок без ограничения общности можно считать, что объем первой из них не превосходит объема второй,  , в противном случае выборки можно поменять местами. Обычно предполагается, что функции
, в противном случае выборки можно поменять местами. Обычно предполагается, что функции  и
и 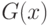 непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью 1 все
непрерывны и строго возрастают. Из непрерывности этих функций следует, что с вероятностью 1 все  результатов наблюдений различны. В реальных эконометрических данных иногда встречаются совпадения, но сам факт их наличия - свидетельство нарушений предпосылок только что описанной базовой математической модели.
результатов наблюдений различны. В реальных эконометрических данных иногда встречаются совпадения, но сам факт их наличия - свидетельство нарушений предпосылок только что описанной базовой математической модели.
Статистика  двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки
двухвыборочного критерия Вилкоксона определяется следующим образом. Все элементы объединенной выборки  упорядочиваются в порядке возрастания. Элементы первой выборки
упорядочиваются в порядке возрастания. Элементы первой выборки  занимают в общем вариационном ряду места с номерами
занимают в общем вариационном ряду места с номерами 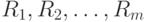 , другими словами, имеют ранги
, другими словами, имеют ранги 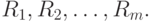 Тогда статистика Вилкоксона - это сумма рангов элементов первой выборки
Тогда статистика Вилкоксона - это сумма рангов элементов первой выборки
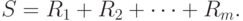
Статистика  Манна-Уитни определяется как число пар
Манна-Уитни определяется как число пар 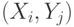 таких, что
таких, что  среди всех
среди всех 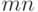 пар, в которых первый элемент - из первой выборки, а второй - из второй. Как известно [13, с.160],
пар, в которых первый элемент - из первой выборки, а второй - из второй. Как известно [13, с.160],

Поскольку  и
и  линейно связаны, то часто говорят не о двух критериях - Вилкоксона и Манна-Уитни, а об одном - критерии Вилкоксона (Манна-Уитни).
линейно связаны, то часто говорят не о двух критериях - Вилкоксона и Манна-Уитни, а об одном - критерии Вилкоксона (Манна-Уитни).
Критерий Вилкоксона - один из самых известных инструментов непараметрической статистики (наряду со статистиками типа Колмогорова-Смирнова и коэффициентами ранговой корреляции). Свойствам этого критерия и таблицам его критических значений уделяется место во многих монографиях по математической и прикладной статистике.
Однако в литературе имеются и неточные утверждения относительно возможностей критерия Вилкоксона. Так, одни полагают, что с его помощью можно обнаружить любое различие между функциями распределения  и
и 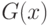 . По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое, строго говоря, неверно. Это будет ясно из дальнейшего изложения.
. По мнению других, этот критерий нацелен на проверку равенства медиан распределений, соответствующих выборкам. И то, и другое, строго говоря, неверно. Это будет ясно из дальнейшего изложения.
Введем некоторые обозначения. Пусть 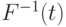 - функция, обратная к функции распределения
- функция, обратная к функции распределения  . Она определена на отрезке
. Она определена на отрезке ![[0;1]](/sites/default/files/tex_cache/06d6c498a68a3b5338e281815cc9fc2d.png) . Положим
. Положим 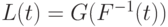 . Поскольку
. Поскольку  непрерывна и строго возрастает, то
непрерывна и строго возрастает, то 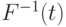 и
и 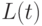 обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина
обладают теми же свойствами. Важную роль в дальнейшем изложении будет играть величина 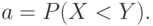 Как нетрудно показать,
Как нетрудно показать,
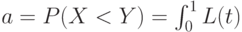
Введем также параметры
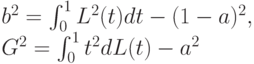
Тогда математические ожидания и дисперсии статистик Вилкоксона и Манна-Уитни согласно [13, с.160] выражаются через введенные величины:
![М(U) = mna , М(S) = mn + m(m+1)/2 - М(U) = mn(1- a) + m(m+1)/2,\\
D(S) = D(U) = mn [ (n - 1) b^2 + (m - 1) g^2 + a(1 -a) ]](/sites/default/files/tex_cache/fa7df27588db8787792209422ba73408.png) |
( 1) |
Когда объемы обеих выборок безгранично растут, распределения статистик Вилкоксона и Манна-Уитни являются асимптотически нормальными (см., например, [13, гл.5 и 6]) с параметрами, задаваемыми формулами (1) .
Если выборки полностью однородны, т.е. их функции распределения совпадают, справедлива гипотеза
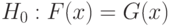 |
( 2) |
 ,
,то  и
и 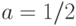 . Подставляя в формулы (1), получаем, что
. Подставляя в формулы (1), получаем, что
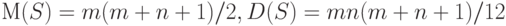 |
( 3) |
Следовательно, распределение нормированной и центрированной статистики Вилкоксона
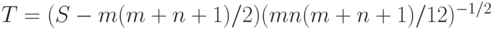 |
( 4) |
при росте объемов выборок приближается к стандартному нормальному распределению (с математическим ожиданием 0 и дисперсией 1).
Из асимптотической нормальности статистики  следует, что правило принятия решения для критерия Вилкоксона выглядит так:
следует, что правило принятия решения для критерия Вилкоксона выглядит так:
- если
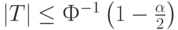 то гипотеза (2) однородности (тождества) функций распределений принимается на уровне значимости
то гипотеза (2) однородности (тождества) функций распределений принимается на уровне значимости 
- если же
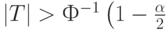 то гипотеза (2) однородности (тождества) функций распределений отклоняется на уровне значимости
то гипотеза (2) однородности (тождества) функций распределений отклоняется на уровне значимости  .
.
В эконометрике наиболее часто применяется уровень значимости 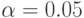 Тогда значение модуля статистики Т Вилкоксона надо сравнивать с граничным значением
Тогда значение модуля статистики Т Вилкоксона надо сравнивать с граничным значением 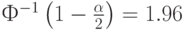 .
.
Пример 1. Пусть даны две выборки. Первая содержит  элементов
элементов  . Вторая содержит
. Вторая содержит 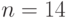 элементов
элементов 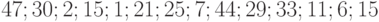 . Проведем проверку однородности функций распределения двух выборок с помощью только что сформулированного правила принятия решений на основе критерия Вилкоксона.
. Проведем проверку однородности функций распределения двух выборок с помощью только что сформулированного правила принятия решений на основе критерия Вилкоксона.
Первым шагом является построение общего вариационного ряда для элементов двух выборок (табл.4.1).
